Дисперсионный анализ экспериментальных данных
Дисперсионный анализ (ДА) служит для оценки значимости влияния отдельных факторов на характер процесса. ДА может быть одно-, двух- и многофакторным. Рассмотрим однофакторный ДА. Результаты проведённого эксперимента представлены на рис. 2.1.
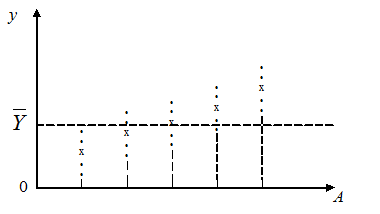
Рисунок 2.1 — Зависимость показаний у от фактора А
На рисунке наблюдается явная зависимость функции y от уровня некоторого фактора A. Модель эксперимента в таком случае может быть представлена в следующем виде:
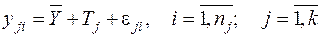 , (2.1)
, (2.1)
где yji — i-е наблюдение над функцией y, когда фактор A находится на j-м уровне (имеет j-е значение);
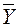 — общее среднее значение функции y в эксперименте;
— общее среднее значение функции y в эксперименте;
Tj — эффект j-го уровня фактора A, т.е. вклад фактора A в величину функции y, когда фактор находится на j-м уровне;
eji — случайная ошибка в i-м наблюдении на j-м уровне;
k — число уровней фактора A;
nj — число наблюдений функции y на j-м уровне фактора A.
Предполагают, что eji — независимые нормально распределённые случайные величины с нулевым средним и не зависящей от уровня фактора дисперсией.
Очевидно, что для данного уровня j фактора A отклонение значения функции yji от общего среднего арифметического 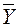 связано с действием на функцию y фактора A. То есть из модели (2.1) можно получить
связано с действием на функцию y фактора A. То есть из модели (2.1) можно получить
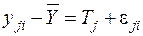 .
.
Величину eji можно ещё представить как остаточную часть отклонения внутри отдельного уровня фактора A, не зависящую от влияния этого фактора. С помощью члена eji учитываются все неконтролируемые факторы, оказывающие случайное воздействие на функцию (признак качества) y.
В ДА рассматриваются две статистические гипотезы:
– нулевая гипотеза H0: эффект фактора равен нулю (Tj = 0), которую проверяют при всех уровнях j;
– альтернативная гипотеза H1: эффект фактора A имеет существенное влияние на выходной параметр процесса y.
Для проверки нуль-гипотезы используется критерий Фишера. Если верна нулевая гипотеза, то никаких эффектов уровней фактора A нет и каждое измерение yji может быть представлено как 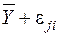 (среднее арифметическое плюс случайная ошибка).
(среднее арифметическое плюс случайная ошибка).
Сущность ДА заключается в разложении суммарной дисперсии, наблюдаемой в опыте, на две: факторную и остаточную и их сравнении.
Факторная дисперсия 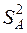 — дисперсия, обусловленная действием изучаемого фактора A.
— дисперсия, обусловленная действием изучаемого фактора A.
Остаточная дисперсия 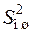 — дисперсия, обусловленная техникой эксперимента, случайным воздействием неконтролируемых факторов.
— дисперсия, обусловленная техникой эксперимента, случайным воздействием неконтролируемых факторов.
Из модели (2.1) получим основное уравнение ДА. Для этого вначале запишем тождество, добавляя 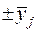 — среднее арифметическое по уровню j (на рис. 2.1 обозначены крестиками):
— среднее арифметическое по уровню j (на рис. 2.1 обозначены крестиками):
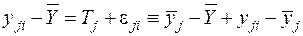 .
.
Таким образом, отклонение наблюдения от общего среднего тождественно отклонению среднего по уровню от общего среднего плюс отклонение наблюдения от среднего по уровню.
Возводим обе части тождества в квадрат и суммируем по всем уровням и наблюдениям.
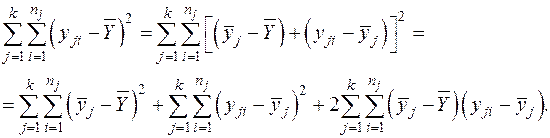
Последнее слагаемое равно нулю, так как его можно записать в следующем виде
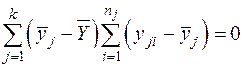 ,
,
вследствие того, что сомножитель 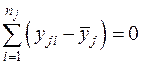 , поскольку он представляет сумму отклонений наблюдений j-й серии от среднего этой же серии (одни отклонения с плюсом, другие с минусом, в результате сумма отклонений равна нулю).
, поскольку он представляет сумму отклонений наблюдений j-й серии от среднего этой же серии (одни отклонения с плюсом, другие с минусом, в результате сумма отклонений равна нулю).
Таким образом, основное уравнение ДА можно записать в следующем виде, введя обозначения для отдельных сумм квадратов отклонений:
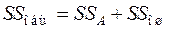 , (2.2)
, (2.2)
где
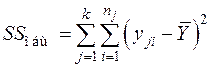 ,
, 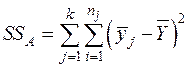 и
и 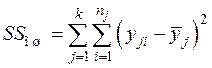 .
.
Это выражение представляет собой разложение суммы квадратов отклонений от общего среднего на сумму квадратов отклонений средних по уровню (испытанию) 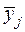 от общего среднего
от общего среднего 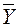 и сумму квадратов отклонений внутри испытаний (правило разложения вариации, см. 1.12).
и сумму квадратов отклонений внутри испытаний (правило разложения вариации, см. 1.12).
Сумма SSобщ называется общей или полной суммой квадратов отклонений отдельных наблюдений от общей средней 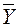 .
.
Сумма SSA называется суммой квадратов отклонений между сериями (или группами). Она характеризует степень расхождения средних по уровням фактора. Её называют также «рассеиванием по уровням фактора» или факторной суммой квадратов.
Сумма SSош характеризует «остаточное рассеивание» случайных погрешностей испытаний и называется остаточной суммой квадратов.
Суммы квадратов отклонений, делённые на соответствующие числа степеней свободы, являются несмещёнными оценками дисперсий: общей 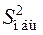 , факторной
, факторной 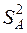 и остаточной
и остаточной 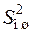 :
:
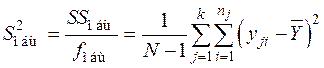 ;
;
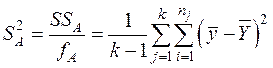 — дисперсия между выборками;
— дисперсия между выборками;
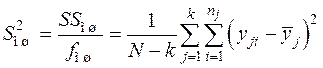 — дисперсия внутри выборок, где
— дисперсия внутри выборок, где 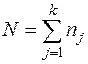 — общее число наблюдений.
— общее число наблюдений.
Дисперсия между выборками 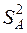 основана на колебании частных средних (средних по выборке
основана на колебании частных средних (средних по выборке 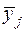 ) вокруг общей средней
) вокруг общей средней 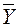 .
.
Дисперсия внутри выборок 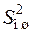 основана на колебании значений наблюдений yji вокруг частной средней
основана на колебании значений наблюдений yji вокруг частной средней 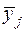 внутри отдельных выборок.
внутри отдельных выборок.
Под выборкой понимается количество наблюдений параметра оптимизации yji при j-м уровне фактора. Если число наблюдений i на всех уровнях одинаково и равно n, то
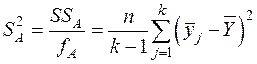 .
.
Общее число наблюдений 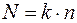 .
.
После определения факторной и остаточной дисперсий необходимо их сравнить с помощью критерия Фишера и принять нулевую или альтернативную гипотезу:
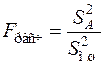 .
.
По таблицам критерия Фишера находят его критическое значение при выбранном уровне значимости a и соответствующем числе степеней свободы fA и fош. Особенностью критерия является то, что в таблицах он всегда больше единицы, следовательно, дисперсия в числителе должна быть больше дисперсии в знаменателе, т.е. если 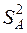 <
< 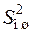 ,то они меняются местами.
,то они меняются местами.
Если Fрасч ³ Fкрит (a, fA, fош), то нулевая гипотеза отвергается. Это значит, что различие между дисперсиями 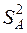 и
и 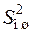 существенно и изучаемый фактор A влияет на признак качества (функцию, выходной параметр и т.п.) y, т.е. влияние фактора A значимо.
существенно и изучаемый фактор A влияет на признак качества (функцию, выходной параметр и т.п.) y, т.е. влияние фактора A значимо.
Если Fрасч < Fкрит (a, fA, fош), то вопрос остаётся открытым и требует дальнейшего исследования. Возможно, что положительный результат может дать увеличение объёма эксперимента. Следовательно, ДА позволяет давать положительный ответ на вопрос о влиянии фактора, но не позволяет давать отрицательный ответ. Однако некоторые авторы, например [10], считают, что если Fрасч < Fкрит, то различие между дисперсиями случайно и исследуемый фактор не влияет на функцию y.
Для уверенности в правильном применении критерия F необходимо, чтобы остаточная дисперсия 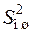 была установлена достаточно основательно, на числе степеней свободы не менее 10, т.е. должно выполняться условие
была установлена достаточно основательно, на числе степеней свободы не менее 10, т.е. должно выполняться условие 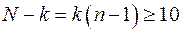 .
.
Для выполнения ДА удобно результаты наблюдений сводить в таблицу (для однофакторного анализа) 2.1.
В практических расчётах значительно легче оперировать с суммами наблюдений, чем со средним. Поэтому удобнее использовать следующие выражения для нахождения сумм квадратов:
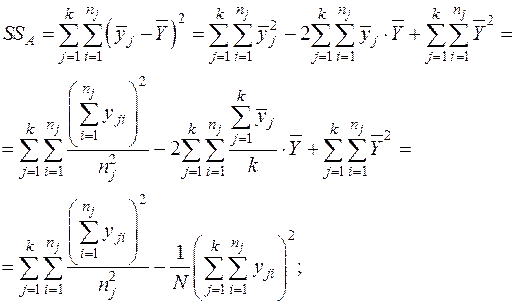
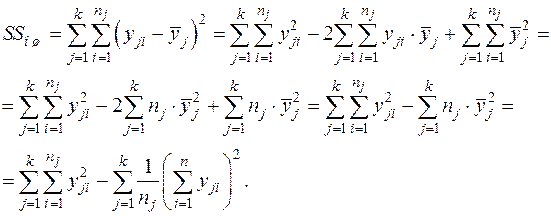
При одинаковом числе наблюдений на каждом уровне, n = const, имеем:
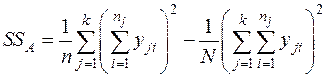 ;
;
 Таблица 2.1
Таблица 2.1
| Уровень фактора | Результаты наблюдений (значения признака качества) | Сумма по уровню (выборка) | Квадрат суммы по уровню | Сумма квадратов наблюдений по уровню | Среднее по уровню (выборке) | ||||||||||||||||
| … | i | … | nj | ||||||||||||||||||
| y11 | y12 | … | y1i | … | 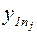 | 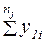 | 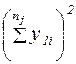 | 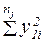 | 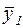 | ||||||||||||
| y21 | y22 | … | y2i | … | 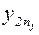 | 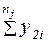 | 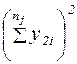 | 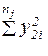 | 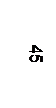 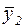 | ||||||||||||
| . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | |||||||||||
| j | yj1 | yj2 | … | yji | … | 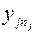 | 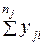 | 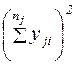 | 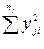 | 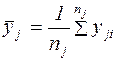 | |||||||||||
| . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | |||||||||||
| k | yk1 | yk2 | … | yki | … | 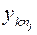 | 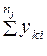 | 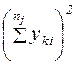 | 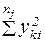 | 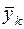 | |||||||||||
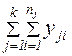 | 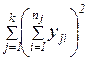 | 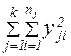 | 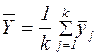 | ||||||||||||||||||
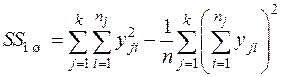 ;
;
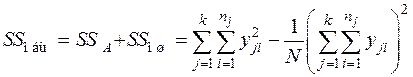 .
.
Результаты ДА не изменятся, если вместо опытных величин y подставить их кодированные значения, но значительно уменьшится порядок цифр и расчёты упростятся.
ДА усложняется при двух и более факторах. Так, при двухфакторном ДА определяются дисперсии по обоим факторам A и B, а также дисперсия по комбинации факторов AB. Затем находят критерии
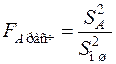 ;
; 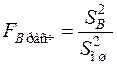 ;
; 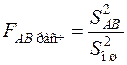 .
.
При многофакторном ДА задача сводится к многократному повторению двухфакторного комплекса.
В заключение отметим, что однофакторный дисперсионный анализ — удобное средство объективной проверки поверхностных суждений и выводов, сделанных на основе средних оценок различных показателей по данным небольшого числа практических наблюдений.
Кроме того, дисперсионный анализ удобен тем, что он позволяет оценивать влияние неизмеряемых качественных факторов на количественные показатели. Например, влияние уровня эксплуатации на показатели надёжности оборудования или влияние квалификации обслуживающего персонала на качество и эффективность профилактической проверки устройств и т.п.
2.3 Корреляционный анализ экспериментальных данных [10]
Корреляционный анализ (КА) используется для установления степени взаимосвязи между параметрами и показателями процесса путём:
1) определения формы связи;
2) определения силы связи.
Корреляционная связь — это такая связь, при которой с изменением одной величины (аргумента) другая величина (функция) изменяет своё среднее арифметическое значение.
Корреляционная связь может быть представлена в аналитической, табличной и графической формах.
Аналитическая форма имеет вид 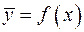 — это корреляционное уравнение (или уравнение регрессии).
— это корреляционное уравнение (или уравнение регрессии).
Табличная форма получается в результате первичной обработки опытных данных, которая заключается в том, что значения наблюдаемых величин разбивают на интервалы и подсчитывают частоты mxy появления этих значений в каждом интервале (рис. 2.2 — фрагмент таблицы).
| х y | х1 … х2 | х2 … х3 | и т.д. | 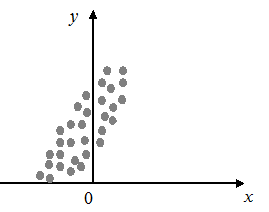 | |
| y1 … y2 | |||||
| y2 … y3 | mxy | ||||
| и т.д. | |||||
| Рисунок 2.2 — Фрагмент корреля- | Рисунок 2.3 — Корреляционное | ||||
| ционной таблицы | поле |
Например, в интервал значений х (10 … 20) и интервал значений y (270 … 300) попало 5 случаев. Это значит, что частота появления пар значений x и y, принадлежащих указанным интервалам, mxy = 5.
Корреляционная связь существует, если частоты располагаются вдоль одной из диагоналей корреляционной таблицы, причём, чем ближе они группируются к диагонали, тем сильнее связь. Если заполняется вся таблица, то никакой связи нет.
Графическая форма представляет собой корреляционное поле, на которое нанесены опытные данные (рис. 2.3).
Следует всегда помнить, что прежде чем приступать непосредственно к КА, необходимо на основании анализа физической сущности исследуемых явлений убедиться в том, что корреляционная связь возможна. Иначе иногда можно вычислить корреляционную связь там, где она физически невозможна.
Оценка существования формы и силы связи между параметрами процесса (например, x и y) производится с помощью коэффициента корреляции rxy и корреляционного отношения 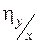 . Анализ свойств коэффициента корреляции rxy и корреляционного отношения показывает, что коэффициент корреляции является мерой тесноты линейной корреляционной связи между параметрами x и y, а корреляционное отношение является мерой тесноты нелинейной корреляционной связи между x и y. В зависимости от значений rxy и
. Анализ свойств коэффициента корреляции rxy и корреляционного отношения показывает, что коэффициент корреляции является мерой тесноты линейной корреляционной связи между параметрами x и y, а корреляционное отношение является мерой тесноты нелинейной корреляционной связи между x и y. В зависимости от значений rxy и 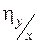 имеют место следующие виды связей (табл. 2.2).
имеют место следующие виды связей (табл. 2.2).
Таблица 2.2
| rxy | 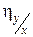 | Характеристика связи |
| rxy = ±1 | – | Линейная функциональная |
| rxy = 0 | 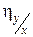 = 1 = 1 | Криволинейная функциональная |
| rxy = 0 | 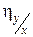 = 0 = 0 | Отсутствует |
| rxy = 0 | 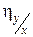 < 1 < 1 | Криволинейная корреляционная |
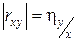 | – | Точная линейная корреляционная |
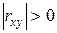 | 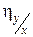 < 1 < 1 | Линейная корреляционная |
Как следует из таблицы, rxy может меняться в пределах от нуля до ±1. Чем он ближе к единице, тем сильнее линейная корреляционная связь, чем он ближе к нулю, тем слабее эта связь.
Корреляционное отношение есть неотрицательная величина, изменяющаяся в пределах от нуля до единицы, и оно не меньше абсолютной величины коэффициента корреляции
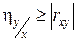 .
.
Визуальная оценка по таблице недостаточна, поскольку в отдельных выборках коэффициенты корреляции и корреляционные отношения могут случайно отличаться друг от друга и от нуля. Поэтому очень важной является оценка реальной связи между переменными. Способ этой оценки зависит от объёма выборки n > 50 или n < 50.
Определение коэффициента корреляции и корреляционного отношения выполняется следующим образом. В результате обработки опытных данных получают корреляционную таблицу (табл. 2.3).
Таблица 2.3
| x y | … | … | i | … | k |  | ||
 x1…x2 x1…x2 | 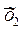 x2…x3 x2…x3 | 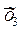 x3…x4 x3…x4 | 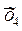 x4…x5 x4…x5 | 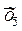 x5…x6 x5…x6 | 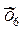 x6…x7 x6…x7 | |||
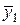 y1…y2 y1…y2 | ||||||||
| . . . | 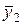 y2…y3 y2…y3 | mxy | ||||||
| j | 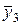 y3…y4 y3…y4 | |||||||
| . . . | 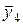 y4…y5 y4…y5 | |||||||
| l | 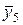 y5…y6 y5…y6 | |||||||
 | n = 55 |
В таблице:
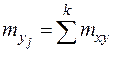 ;
; 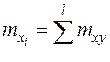 ;
;
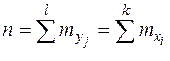 — объём выборки;
— объём выборки;
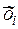 и
и 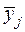 — средние значения x и y в интервалах;
— средние значения x и y в интервалах;
k и l — количество интервалов соответственно для x и для y.
Из таблицы уже видна корреляционная связь между переменными x и y: с ростом переменной x растёт и переменная y.
Порядок расчёта rxy и 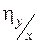 следующий.
следующий.
1. Определяются средние значения x и y в выборке
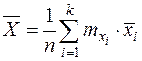 ;
; 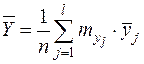 .
.
2. Находят средние квадратические отклонения для x и y в выборке
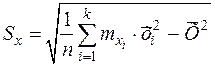 ;
; 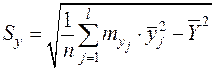 .
.
3. Определяют ковариацию (корреляционный момент)
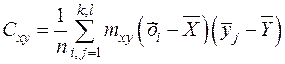
или более просто
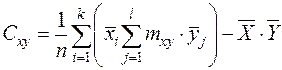 .
.
4. Определяют коэффициент корреляции
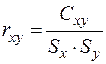 .
.
5.Определяют корреляционное отношение
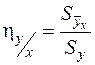 ,
,
где 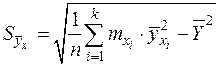 и
и 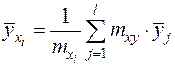 .
.
Далее оценивают достоверность (надёжность) вычисленных коэффициента корреляции и корреляционного отношения. При числе наблюдений n ³ 50 поступают следующим образом. Определяют средние квадратические ошибки коэффициента корреляции и корреляционного отношения
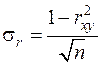 и
и 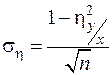 .
.
Затем определяют отношения 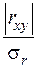 и
и 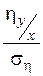 . Если эти отношения больше трёх (у некоторых авторов — четырёх), то rxy и
. Если эти отношения больше трёх (у некоторых авторов — четырёх), то rxy и 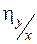 можно считать достоверными.
можно считать достоверными.
Доверительные интервалы, в которых находятся истинные (генеральные) значения rxy и 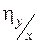 , можно определить, задавшись уровнем значимости a или надёжностью вывода p = 1 – a по формулам
, можно определить, задавшись уровнем значимости a или надёжностью вывода p = 1 – a по формулам
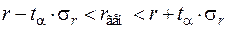 и
и 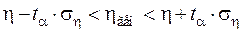 ,
,
где ta определяется по таблице интеграла вероятностей (функции Лапласа) по значению p.
Если нижняя граница r – tasr будет мала, то нет оснований считать величины x и y в генеральной совокупности связанными линейной корреляционной связью.
При n < 50 используется иной способ оценки надёжности rxy и 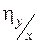 [3, 10].
[3, 10].
