II.3. Внутренняя энергия и теплоёмкость идеального газа
Используем уравнение состояния идеального газа pv = RT для нахождения частных производных 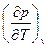 ,
, 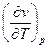 входящих в уравнения (74) и (75):
входящих в уравнения (74) и (75):
Для этого продифференцируем уравнение Менделеева-Клайперона pv=RT:
p dv + v dp = R dT, откуда имеем
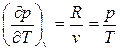 (77)
(77)
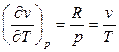 (78)
(78)
Подставим в (73*) значение 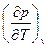 из уравнения (77) для идеального газа:
из уравнения (77) для идеального газа:
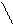
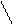
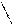
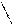
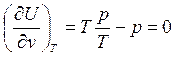
Окончательно
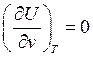 (79)
(79)
Таким образом, внутренняя энергия идеального газа от величины объёма не зависит. Математически этот факт записывается как
U¹U(v) (79*)
Исследуем вопрос о зависимости внутренней энергии идеального газа от величины давления. Найдем частную производную 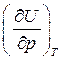 , для чего запишем ее в виде произведения двух частных производных:
, для чего запишем ее в виде произведения двух частных производных:
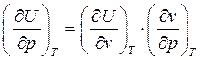
Из (79) 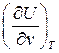 =0. Изотермическая сжимаемость по своей физической сути величина конечная, т.е.
=0. Изотермическая сжимаемость по своей физической сути величина конечная, т.е. 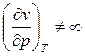 .
.
Тогда окончательно
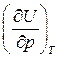 =0 (80)
=0 (80)
Из формулы (80) следует, что внутренняя энергия идеального газа не зависит от величины давления, то есть U¹U(р)
Следовательно, внутренняя энергия идеального газа зависит только от температуры.
Ранее было получено
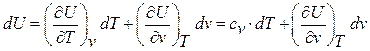
Так как из (79) 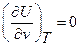 , то
, то
dU = cv dT (81)
Интегрируя (81) получим:
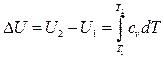 (82)
(82)
Общая формула (82) – используется для расчета изменения внутренней энергии во всех процессах идеального газа. Для вычисления по этой формуле нужно знать зависимость Сv от Т.
 Если в диапазоне температур от T1 до T2, cv взять средним значением (сv), то, после интегрирования (82) получим
Если в диапазоне температур от T1 до T2, cv взять средним значением (сv), то, после интегрирования (82) получим
 DU = cv(T2-T1) (83)
DU = cv(T2-T1) (83)
Формула (83) в дальнейшем будет использоваться в инженерных расчетах для определения изменения внутренней энергии идеального газа в любом процессе.
Значение внутренней энергии из (81) после интегрирования запишется как 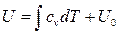 , где U0 – постоянная интегрирования, определяемая особым образом.
, где U0 – постоянная интегрирования, определяемая особым образом.
Получим формулу для массовой изобарной теплоёмкости идеального газа. Подставим в формулу (75)
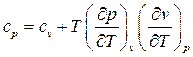 , значения частных производных из (77) и (78):
, значения частных производных из (77) и (78):


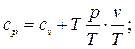
Окончательно
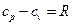 (85)
(85)
Формула (85) называется уравнением Майера. Из этой формулы следует, что массовая изобарная теплоёмкость больше массовой изохорной теплоёмкости идеального газа на величину удельной газовой постоянной R.
Для мольных теплоёмкостей уравнение Майера запишется в виде:
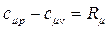 = 8314
= 8314 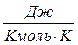 (86)
(86)
Таким образом молярная изобарная теплоемкость больше молярной изохорной на величину универсальной газовой постоянной.
Отношение изобарной теплоемкости к изохорной называется показателем адиабаты
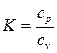 (87)
(87)
Иногда показатель адиабаты называют коэффициентом Пуассона. В соответствие с уравнением Майера К > 1.
В инженерных расчетах для всех двухатомных газов, включая воздух, полагают K»1,4.
В действительности, с ростом температуры показатель адиабаты слабо убывает.
