Передача тепла теплопроводностью

Процесс передачи тепла теплопроводностью описывается с помощью закона Фурье, согласно которому количество тепла dQ, передаваемое посредством теплопроводности через элемент поверхности dS, перпендикулярный тепловому потоку, за время dτ,прямо пропорционально температурному градиенту dt/dn поверхности dS ивремени dτ:

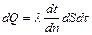, (1.2)

где λ – коэффициент теплопроводности; является теплофизической характеристикой, зависит от наличия любых примесей (влага, воздух), структуры материала, температуры, давления (не всегда).

Коэффициент теплопроводности λ имеет размерность: 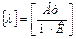и показывает, какое количество тепла переносится путем теплопроводности в единицу времени через единицу поверхности теплообмена при падении температуры на 1 градус на единицу длины нормали к изотермической поверхности.

Для характеристики теплоинерционных свойств вещества введем понятие коэффициента температуропроводности а. Чем больше величина а у вещества, тем быстрее оно нагревается или охлаждается:

.

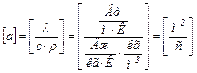Передача тепла конвекцией

Интенсивность переноса тепла конвекцией зависит от степени турбулентности потока жидкости и перемешивания частиц внутри него. Следовательно, конвекция сильно зависит от гидродинамических условий течения потока жидкости.

В ядре потока перенос тепла осуществляется одновременно теплопроводностью и конвекцией. Совместный перенос тепла этими способами называется конвективной теплоотдачей. Механизм переноса тепла в ядре потока при его турбулентном движении характеризуется интенсивным перемешиванием макрообъемов среды, которое приводит к выравниванию температур до некоторого среднего значения t_ж. По мере приближения к стенке интенсивность теплоотдачи падает. Это объясняется тем, что вблизи нее образуется тепловой пограничный слой, подобный гидродинамическому пограничному слою, но обычно меньше его по толщине. В этом слое по мере приближения к стенке все большее значение приобретает теплопроводность, а влияние турбулентности становится пренебрежимо мало.

Сложность механизма конвективного теплообмена обусловливает трудности расчета процесса теплоотдачи. Точное решение задачи о количестве тепла, передаваемого от стенки к среде, связано с необходимостью определения температурного градиента у стенки и профиля изменения температур теплоносителя вдоль поверхности теплообмена, что весьма затруднительно. Поэтому за основу непрерывного процесса теплоотдачи принимают уравнение Ньютона:

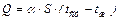, (1.3)

где α – коэффициент теплоотдачи, который показывает, какое количество тепла передается от 1 м² поверхности стенки к жидкости в течение 1 секунды при разности температур между стенкой и жидкостью 1 градус.

Коэффициент теплоотдачи зависит от следующих факторов:

– скорости жидкости w, ее плотности ρ и вязкости μ,т.е. переменных, определяющих режим течения жидкости;

– тепловых свойств жидкости (удельной теплоемкости Ср, теплопроводности λ, коэффициента объемного расширения β);

– геометрических параметров – формы и определяющих размеров стенки (для труб – их диаметра d и длины L, шероховатости ε).

Таким образом:

α = f(W, μ, ρ, c_p, λ, β, d, L, ε). (1.4)

Отсюда видно, что простота уравнения (1.3) только кажущаяся. Трудность заключается в расчете величины α. Кроме того, невозможно получить расчетное уравнение, пригодное для всех случаев теплоотдачи. Только путем обобщенных опытных данных с помощью теории подобия можно получить обобщенные (критериальные) выражения для типовых случаев теплоотдачи, позволяющие рассчитать коэффициент теплоотдачи для конкретных условий. Исходной зависимостью для этого является общий закон распределения температур в жидкости, выраженный дифференциальным уравнением конвективного теплообмена:

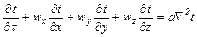. (1.5)

Это уравнение выражает, в общем виде, распределение температур в движущемся потоке. Его называют также дифференциальным уравнением Фурье-Кирхгофа.

При расчете конвективного теплообмена обычно используют путь, заключающийся в том, что расчетные выражения получают из общих дифференциальных уравнений, применяя методы теории подобия, и приводят их к конкретному виду с помощью экспериментальных данных.

Тепловое подобие

Подобие граничных условий описывается с помощью критерия Нуссельта: .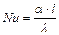

В данный критерий входит определяемая в задачах по конвективному теплообмену величина .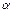

Условие подобия в ядре потока описывается с помощью критерия Фурье, который характеризует связь между скоростью изменения температурного поля, размерами канала, в котором происходит теплообмен, и физическими свойствами среды в нестационарных условиях: .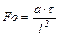

Критерий Пекле показывает соотношение между количеством тепла, переносимым путем конвекции и теплопроводности при конвективном теплообмене: .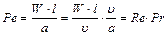

Критерий Прандтля характеризует поле теплофизических величин потока жидкости: .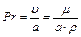

Критерий Грасгофа вводится при теплообмене в условиях естественной конвекции и показывает меру отношения сил трения к подъемной силе, определяемой разностью плотностей в различных точках потока:

,

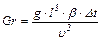где β –коэффициент объемного расширения жидкости, К^-1;

∆t – разность температур горячих и холодных частиц жидкости, вызывающих естественную конвекцию, К.

Необходимыми условиями подобия переноса тепла является соблюдение гидродинамического и геометрического подобия. Первое характеризуется равенством критериев Re в сходственных точках подобных потоков, второе - постоянством отношения основных геометрических размеров стенки L₁, L₂, … ,L_n к некоторому характерному размеру.

Таким образом, с учетом того, что критерий Nu является определяемым, т.к. в него входит искомая величина коэффициента теплоотдачи α, критериальное уравнение конвективного теплообмена выражается в виде:

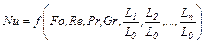. (1.6)

Вид функции (1.6) определяется опытным путем, причем обычно ей придают степенную форму. Например, при движении потока в трубе диаметром d идлиной l уравнение (1.6) примет вид:

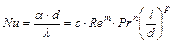, (1.7)

где величины с, т, п, р определяются по опытным данным.

Коэффициент теплоотдачи 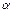определяется по найденному из критериальных уравнений критерию Нуссельта.