Теоретическая часть. Марковские случайные процессы

ЛАБОРАТОРНАЯ РАБОТА №2

Марковские случайные процессы

Подготовительная часть

Для выполнения лабораторной работы необходимо повторить вопросы, связанные с определениями: случайный процесс, марковский процесс, граф состояний, поток событий, вероятности состоя­ния, уравнения Колмогорова, финальные вероятности состояний.

Теоретическая часть

Пример. Пусть нормально работающая система (состояние 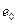) подвергается простейшему потоку отказов с интенсивностью 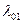, переходя в новое состояние 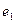, в котором она некоторое время может работать с необнаруженным отказом. Как только отказ обнаруживается (интенсивность обнаружения 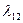), производится осмотр системы (состояние 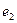). В результате осмотра, система либо направляется в ремонт (состояние 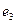) с интенсивностью 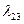, либо списывается и заменяется новым (состояние 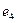) с интенсивностью 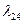. Из состояния 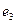с интенсивностью 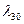и из состояния 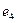с интенсивностью 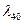система переходит в рабочее состояние 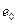. Найти распределение вероятностей состояний для любого момента времени и финальные вероятности состояний.

Решение.

Марковский процесс с дискретными состояниями удобно иллюстрировать с помощью размеченного графа состояний. Граф состояний для сформулированной задачи приведен на рис. 1.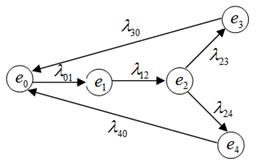

Рис. 1. Размеченный граф состояний системы

Пользуясь размеченным графом состояний системы, составим систему дифференциальных уравнений Колмогорова:

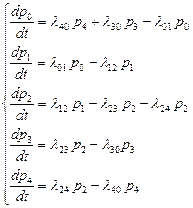
и нормировочное условие .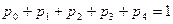

Для определенности придадим параметрам, приведенным в системе дифференциальных уравнений, следующие значения:

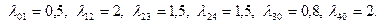
Зададим также начальные условия, т.е. распределение вероятностей состояний в начальный момент времени:

.

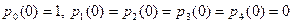В результате получим систему линейных дифференциальных уравнений с постоянными коэффициентами:

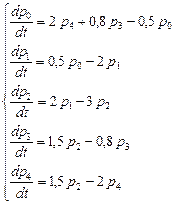
Данную систему линейных дифференциальных уравнений с постоянными коэффициентами решим методом Рунге-Кутта:

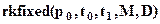, где 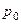- начальные условия, 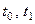- начальная и конечная точки расчета соответственно, 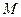- число шагов, 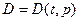- матричная форма правых частей системы дифференциальных уравнений.

Листинг с введенными параметрами и полученным результатом решения в системе MathCAD представлен на рис.2.

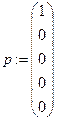
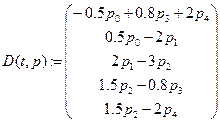
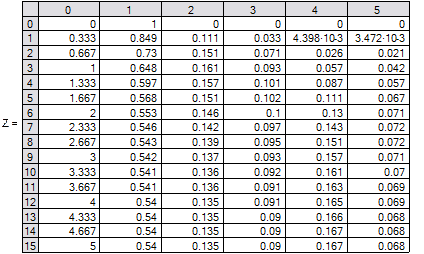
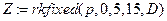
Рис. 2. Решение системы дифференциальных уравнений

Из решения (рис. 2) следует, что спустя период времени 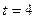наступает стабилизация случайного процесса.

Для проверки решения системы дифференциальных уравнений на устойчивость целесообразно воспользоваться функцией отыскания собственных чисел 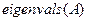, имеющейся в системе MathCAD. Результаты вычисления вектора собственных чисел матрицы 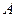приведены ниже:

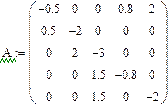
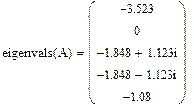
Принимая во внимание теорему об устойчивости решений системы линейных однородных дифференциальных уравнений первого порядка с постоянными коэффициентами, заметим, что корни характеристического уравнения матрицы 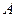не имеют положительных действительных частей, следовательно, полученное решение устойчиво.

Проблема устойчивости для данного класса задач является актуальной, так как предполагается нахождение финальных вероятностей для стохастических систем, описываемых с помощью дифференциальных уравнений Колмогорова.

Для вычисления финальных вероятностей положим левые части в системе дифференциальных уравнений Колмогорова равными нулю, получим однородную систему линейных алгебраических уравнений. Принимая во внимание нормировочное условие для вероятностей, и отбрасывая одно из уравнений системы, получим неоднородную систему линейных уравнений. Для решения системы средствами MathCAD воспользуемся функцией 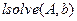. Результаты вычисления финальных вероятностей приведены ниже

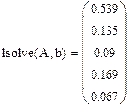При этом финальные вероятности можно истолковать как среднее время пребывания системы в данном состоянии. Данная система в среднем 54% времени будет работать нормально, 13,5% времени работать с необнаруженным отказом, 9% времени будет затрачено на диагностику, 17% времени на ремонт и около 7% тратится на замену новым оборудованием.

Знание финальных вероятностей можно использовать для оценки эффективности работы системы. Для этого достаточно задать вектор стоимостей пребывания системы в каждом из состояний, которые можно интерпретировать как доход или расход в единицу времени. Тогда в предельном, стационарном режиме средний доход в единицу времени 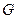будет вычисляться как скалярное произведение вектора финальных вероятностей 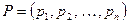на вектор стоимостей 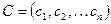, т.е. 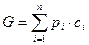, где n- число состояний системы.