Граничные условия для дополнительных напряжений
На поверхности L граничные условия определяются формулами:
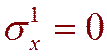 ,
, 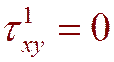 (6.8)
(6.8)
На контуре L1:
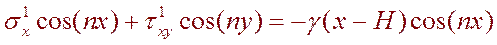 (6.9)
(6.9)
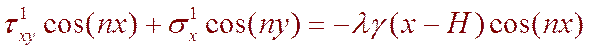
Составляющие дополнительных напряжений превращаются в нуль на бесконечности. Так как выработка находится на глубине H>> x, величиной координаты x по сравнению с превосходящей её величиной H можно пренебречь и уравнения (6.9) принимают более простой вид
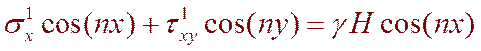 (6.9)
(6.9)
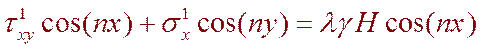
Кроме того, можно отказаться от граничных условий (6.4) и (6.8), рассматривая напряжения не в полуплоскости а в плоскости. Такое предположение справедливо, так рассматриваются напряжения в окрестности выработки. Доказано, что влияние свободной от напряжений земной поверхности можно не учитывать, если выработке находится на глубине, удовлетворяющей неравенству:
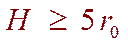 .
.
Задача Кирша
Задачу распределения напряжений вокруг круглого отверстия в бесконечной пластине является одной из наиболее простых в теории упругости. можно решить разными способами
Решить её можно различными способами (например с использованием комплексных потенциалов Колосова-Мусхелишвили 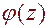 и
и 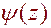 ).
).
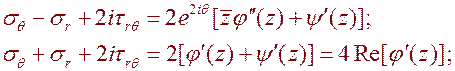
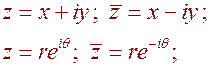
Задача распределения напряжений вокруг круглого отверстия в бесконечной пластине была решена Киршем в 1898 году.
Задача просто решается с использованием функций напряжений Эйри (датский астроном).
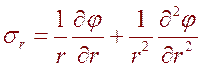 (6.10)
(6.10)
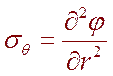
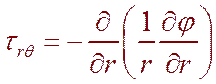
Решение уравнения (6.10) можно представить в виде:
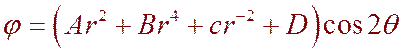 (6.11)
(6.11)
Постоянные интегрирования A B C и D определяются из граничных условий. Опуская промежуточные математические преобразования, приведём формулы для напряжений:
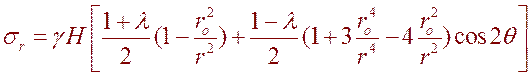 ,
,
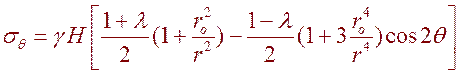 , (6.12)
, (6.12)
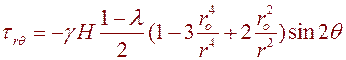 .
.
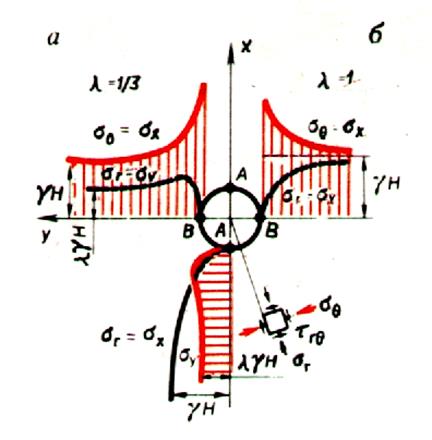
6.3. Распределение напряжений вокруг выработок круглого
сечения
При λ=1 (гидростатическое поле напряжений) напряжения вокруг выработки определяются
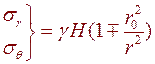 ,
, 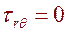 , (6.13)
, (6.13)
Напряжения не зависят от угла (полярная симметрия). Напряжения зависят только от радиуса r и не зависят от угла q.
Нормальные тангенциальные напряжения постоянные и определяются выражением:
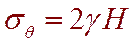 (6.14)
(6.14)
Упражнения и вопросы
1. Определить выражения для определения напряжений на контуре выработки, т.е. при r=r0.
2. Определить напряжения в точке контура выработки при θ=0 и θ=π (на концах вертикального диаметра)
3. При каких условиях в этой точке возникают растягивающие напряжения, при каком коэффициенте Пуассона?
4. Определить напряжения в точке контура выработки при θ= π/2 и θ= 3π/2 (на концах горизонтального диаметра).
5. При каком значении λ достигаются максимальные напряжения сжатия на концах горизонтального диаметра.
6. Какова величина максимального коэффициента концентрации сжимающих напряжений?
7. На каком расстоянии от выработки влиянием её на напряжённо деформированное состояние массива породы можно пренебречь?
Ответы на упражнения и вопросы
1. Определить выражения для определения напряжений на контуре выработки, т.е. при r=r0.
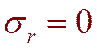 ,
, 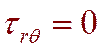
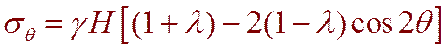 ,
,
2. Определить напряжения в точке контура выработки при θ=0 и θ=π (на концах вертикального диаметра)
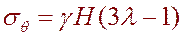
3. При каких условиях в этой точке возникают растягивающие напряжения, при каком коэффициенте Пуассона?
Ответ: λ<1/3. 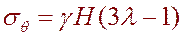
4. Определить напряжения в точке контура выработки при θ= π/2 и θ= 3π/2 (на концах горизонтального диаметра).
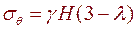
5. При каком значении λ достигаются максимальные напряжения сжатия на концах горизонтального диаметра. Максимальный коэффициент имеет место в безраспорном массиве концентрации при λ=0
Ответ при λ=0 «безраспорный массив» и 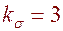 .
.
6. Какова величина максимального коэффициента концентрации сжимающих напряжений? Ответ 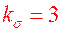 .
.
7. На каком расстоянии от выработки влиянием её на напряжённо деформированное состояние массива породы можно пренебречь? 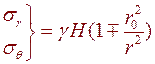
6.3. Выработки мелкого заложения
В предыдущих параграфах рассмотрены случаи заглубленных выработок, для которых справедливо соотношение (рис. 6.4 H>>r0.
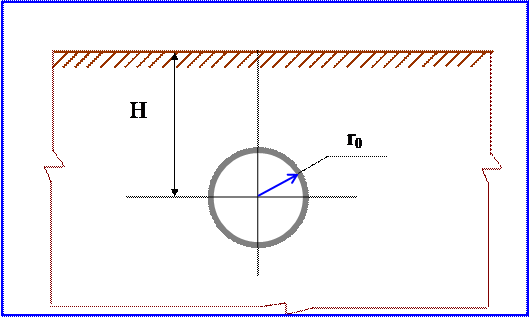
Рис.6.4. Выработка мелкого заложения
Поле начальных напряжений в окружающем выработку массиве в этом случае принимается однородным (  ).
).
Для выработки неглубокого заложения глубина H соизмерима с радиусом r0, поэтому на напряженно-деформированное состояние массива в окрестности выработки существенное влияние оказывает близость земной поверхности L. В этом случае геометрической моделью массива служит уже не плоскость, а полуплоскость.
Решения подобного класса задач получены И.Г. Арамановичем, А.М. Гольдбергом и др.
Нормальные тангенциальные напряжения на контуре сечения выработки круглого сечения описываются формулой:
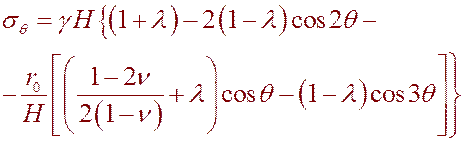 (6.15)
(6.15)
Сравнивая с выражением, полученным ранее (см. предыдущую лекцию) убеждаемся, что первая часть формулы представляет собой величину напряжений для заглубленной выработки.
На рис. (6.5) показаны эпюры нормальных тангенциальных напряжений на контуре сечения выработки при H=2r0; v=0,4, вычисленных по формулам (6.4) и формулам для выработки глубокого заложения. Коэффициент бокового давления λ=0,67 определен по формуле:
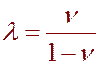
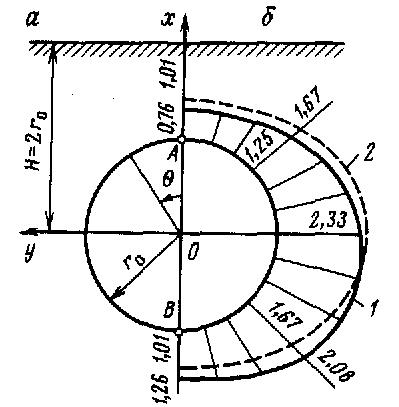
Рис.6.5. Расчетная схема–левая сторона рисунка; эпюры тангенциальных напряжений 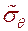 на контуре сечения выработки правая сторона рисунка.
на контуре сечения выработки правая сторона рисунка.
Кривая 1– напряжения 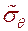 с учетом влияния близости земной поверхности;
с учетом влияния близости земной поверхности;
Кривая 2– напряжения 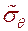 для заглубленной выработки.
для заглубленной выработки.
Существенное влияние на напряженно-деформированное состояние незаглубленной выработки оказывает нагрузка q, приложенная на земной поверхности (рис. 6.5).
В таблице №1 приведены значения нормальных тангенциальных напряжений 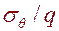 на контуре сечения выработки при различных значениях глубины заложения выработки
на контуре сечения выработки при различных значениях глубины заложения выработки 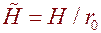 и протяженности участка приложения нагрузки
и протяженности участка приложения нагрузки 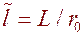 .
.
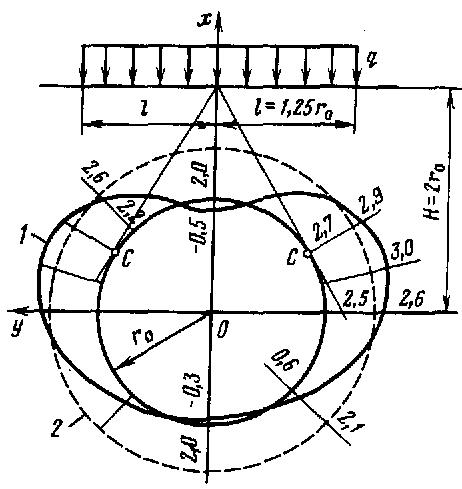
Рис. 6.5. Эпюры нормальных тангенциальных напряжений на контуре сечения выработки мелкого заложения под действием нагрузки, приложенной к земной поверхности при H=2ro:
Кривая 1 – при l=1,25ro;
Кривая 2 – при  .
.
Таблица 1. Касательные напряжения на контуре выработки.
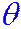 (градус) (градус) | 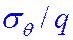 при значениях при значениях 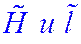 | |||||
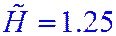 | 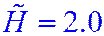 | |||||
 =0.31 =0.31 |  =1.25 =1.25 |  =10 =10 |  =0.5 =0.5 |  =2.0 =2.0 |  =16 =16 | |
| -3.597 | -1.797 | 1.438 | -1.00 | -0.52 | 1.58 | |
| 3.73 | 4.85 | 5.30 | 0.642 | 1.03 | 2.14 | |
| 2.13 | 5.41 | 4.76 | 1.32 | 2.91 | 2.70 | |
| 0.793 | 2.91 | 3.46 | 0.946 | 2.65 | 2.69 | |
| 0.171 | 1.01 | 2.50 | 0.309 | 1.27 | 2.26 | |
| -0.126 | -0.049 | 1.62 | -0048 | 0.115 | 1.65 | |
| -0.209 | -0.394 | 1.23 | -0.171 | -0.314 | 1.35 |
При  , т.е. в случае, когда вся упругая полуплоскость с отверстием равномерно сжата внешней нагрузкой q, тангенциальные напряжения на контуре отверстия описываются выражением
, т.е. в случае, когда вся упругая полуплоскость с отверстием равномерно сжата внешней нагрузкой q, тангенциальные напряжения на контуре отверстия описываются выражением
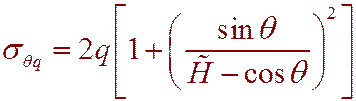 (6.16)
(6.16)
Напряжения только сжимающие. Максимальные напряжения действуют в точках C (рис. 2), в которых контурная окружность касается сторон описанного угла с вершиной в точке пресечения оси x с земной поверхностью.
Максимальные напряжения
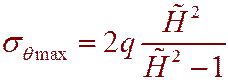 (6.17)
(6.17)
Минимальные напряжения имеют место в своде и лотке выработки:
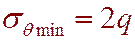 (6.18)
(6.18)
Взаимное влияние выработок. Упругая модель массива позволяет исследовать взаимное влияние выработок. Алгоритмы и программа расчета напряжений в массиве при произвольном количестве взаимовлияющих параллельных выработок круглого сечения и произвольном их расположении при различных видах воздействий разработан Н.Н. Фотиевой и А.Н. Козловым, для выработок некруглого сечения – Р.А. Дунаевским.
На рис. 6.6 показана расчетная схема и распределение напряжений в целике между двумя выработками круглого сечения.
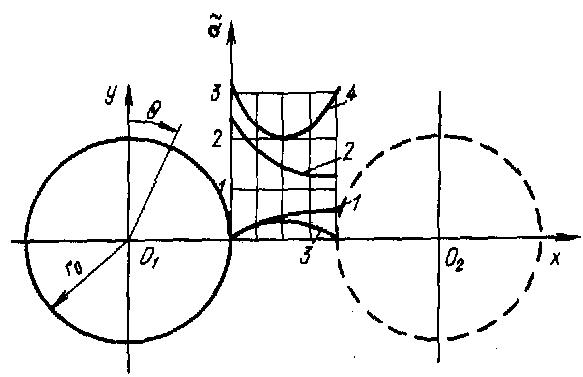
Рис. 6.6. Схема к определению напряжений в целике между двумя выработками.
Кривые 1, 2 – напряжения 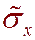 и
и 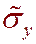 при одиночной выработке с центром O1;
при одиночной выработке с центром O1;
Кривые 3, 4 – напряжения 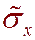 и
и 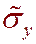 в целике после проходки второй выработки (O2).
в целике после проходки второй выработки (O2).
