Кешенді сандар өрісі

Өрістің кешенді кеңеюі. F=(F, +, -, *. 1) – өріс және t – F алаңына жатпайтын элемент (белгі) болсын. a+bt түрін, мұндағы a мен b – F өрістің туынды элементтері, оларды F алаңының үстіндегі t-дан басталатын жолақтық көпмүше деп атайық (немесе форма). a және b бөлшектері a+bt көпмүшесінің коэффиценттері деп аталады.

t-дан басталатын жолақты көпмүше тең деп аталады, егер олар бір қосындыдан тұрса (бірдей коэффицент), мағынадан алынып тасталынуы мүмкін (форма үшін) нөлдік коэффицентті қосындыға дейін дәл болған жағдайда. Негізінен кез келген бөлшектер үшін a мен b F алаңында

(І) a+0*t=a, 0+bt=bt

F алаңындағы t-дан басталатын барлық жолақтық көпмүшелердің жинақтарын К арқылы белгілейік:

K={a+bt|a, b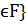

К жинағымен +, -, * операцияларын келесі формулалар арқылы анықтаймыз:

(II) (a+bt)+(c+dt)=(a+b)+(b+d)t

(III) -(a+bt)=(-a)+(-b)t

(IV) (a+bt)*(c+dt)=(ac-bd)+(ad+bc)t.

K = {K, +, -, *, 1}, мұндағы 1 – F өрістің бірлігі, алгебрасын жолақтық көпмүшелер алгебрасы деп атайық.

ТЕОРЕМА 7.1. 1) F=(F, +, -, *, 1) – алаң. K = {K, +, -, *, 1} F өрістің жолақтық көпмүшелер алгебрасы коммутативті шеңбер болып табылады, ал F өрісін оның шеңбершесі болады.

Дәлелдеу. K алгебрасының басты операциялары Fөрісінің сәйкес басты операцияларының жалғасы болып табылады. Шынымен, (І) – (IV) формулаларға байланысты кез келген a мен b F-дан

a+b=(a+0*t)+(b+0*t)=(a+b)+ 0 *t=a+b;

-a=-(a+0*t)=(-a)+0*t=-a;

a*b=(a+0*t)*(b+0*t)=a*b+0*t=a*b;

Сонымен қатар, K алгебрасының 1 элементі F өрісінің бірлігі болып табылады. Сәйкесінше, F алаңы K алгебрасының подалгебрасы болып табылады.

F 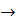K

(К, +, -) алгебрасы – абелев тобы. Шынымен, K алгебрасындағы қосынды ((ІІ) формула бойынша) коммутативті және ассоциативті, себебі F алаңында коммутативті және ассоциатвті қосынды болып табылады. F алаңының нөлі K алгебрасындағы қосындыға қатысты бейтарап болып табылады, себебі (І), (ІІ) формулаларға байланысты K -дағы a+bt кез келген элементі үшін

(a+b*t)+0=(a+b*t)+(0+0*t)=(a+bt)

K -дағы a+bt кез келген бөлшегі қарама-қарсылыққа ие, себебі (a+b*t) + ((-a) + (-b)*t)=0+0*t=0. Осылайша, (К, *, 1) алгебрасы абелев тобы екендігі анықталды.

(К, *, 1) алгебрасы коммутативті моноид болып табылады. Шынымен де, K -дағы көбейтінді ((ІV) формула бойынша) F алаңындағы көбейтіндінің коммутативтілігіне байланысты коммутативті. Ассоциативті көбейтіндіні тексереміз Алгебрадағы K үшін:

(a+b*t)*[(c+dt)*(e+ft)]=(a+bt)[(ce-df)+(cf+de)t]=(ace-adf-bcf-bde)+(acf+ade+bce-bdf)t;

[(a+bt)*(c+dt)]*(e+ft)=[(ac-bd)+(ad+bc)t](e+ft)=(ace-bde-adf-bcf)+(acf-bdf+ade+bce)t.

Сәйкесінше,

(a+bt)*[(c+dt)*(c+ft)]=[(a+bt)(c+dt)](e+ft).

F алаңының бірлігі K алгебрасындағы көбейтіндіге қатысты бейтарап элемент, себебі:

(a+bt)*1=(a+bt)(1+0*t)=a+bt.

Осылайша, (К, *, 1) алгебрасы коммутативті моноид екені анықталды.

K алгебрасындағы көбейтінді косындыға қатысты дистрибутивті болып табылады. Шынымен де:

[(a+bt)+(c+dt)]*(e+ft)=[(a+c)+(b+d)t](e+ft)=(ae+ce-bf-df)+(af+cf+be+de)t;

(a+bt)*(e+ft)+(c+dt)*(e+ft)=[(ae-bf)+(af+be)t]+[(ce-df)+(cf+de)t]=(ae-bf+ce-df)+(af+be+cf+de)t.

Сәйкесінше,

[(a+bt)+(c+dt)]*(c+ft)=(a+bt)*(e+ft)+(c+dt)*(e+ft).

Сонымен, K алгебрасы кoммутативті шеңбер екендігі дәлелденді. (1)-ге байланысты F өрісін K шеңберінің шеңбершесі болып табылады.

АНЫҚТАМА. F=(F, +, -, *. 1) әрбір элементі квадраты -1-ден ерекше өріс болсын. Егер келесі шарттар орындалса, K алаңы F алаңының кешенді кеңейтілуі деп аталады:

(1) F K -ныңөрістің өрісшесі;

(2) K -дамынадай элемент бар u, ол u²=-1;

(3) K өрістің әрбір элементі z z=a+bu түрінде беруге болады, мұндағы a,b 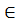F

ҰСЫНЫС.7,2 F алаңы, әрбір элементтің квадраты -1-ден ерекше болсын. K F өрістің кешенді кеңейтілуі және u –алдыңғы анықтамалардың (2) және (3) шарттарын қанағаттандыратын K өрістің элементі болсын. Сонда K өрістің кез келген бөлшегі z-ті жалғыз рет қана z=a+bu түрінде беруге болады, мұндағы a, b 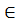F

Дәлелдеу. Z K алаңының кез келген элементі болсын. z-тің екі туынды ерікті туындысын түрінде қарастырайық:

(4) z=a+bu, z=c+du,

мұндағы a,b,c,d 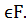Егер b 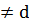болса, онда a+bu=c+du және u= 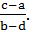Сәйкесінше, u= 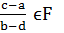және 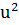=-1 Алайда бұл F өрістің әрбір элементінің квадраты -1-ден ерекше шартына қарсы келеді. Осылайша, жағдайы мүмкін емес. Сәйкесінше, b=d және (4) a=c. байланысты

ТЕОРЕМА.7,3 F=(F, +, -, *. 1) әрбір элементтің квадраты -1-ден ерекше өріс болсын. Онда F өрістің кешенді кеңеюі мүмкін.

Дәлелдеу. К – t айнымалысы бар F алаңындағы барлық жолақты көпмүшелердің жиынтығы болсын:

(1) K={a+bt|a,b

К жиынтығына теңдік пен +, -, * операцияларының қатынасы (І) – (V) формулаларының көмегімен анықталады. Жоғарыдағы теоремасы бойынша K алгебрасы:

K =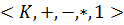

Коммутативті шеңбер бар және Ғ өрісі K шеңберінің шеңбершесі болып табылады:

(2) F

K шеңбері өріс екенін дәлелдейік. (2)-ге байланысты ноль мен F алаңының бірлігі ноль және K шеңберінің бірлігі болып табылады, сондықтан 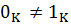. Бізге К-дағы кез келген нолдік емес элемент үшін K -да оған қарама-қарсы бар екенін көрсету ғана қалады. a+b 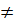0 болсын, мұндағы a, b 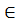F. Онда a 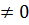немесе b≠0 . Сондықтан 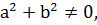, себебі кері жағдайда 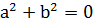және (a/b)²=-1 ( 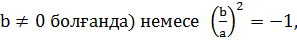ал ол теорема шарты бойынша мүмкін емес. (ІІ) және (V) формулаларына байланысты бізде бар:

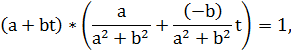
Яғни, элемент a+bt K—да қарсы сипатқа ие. Сәйкесінше, K шеңбері өріс болып табылады.

К-дағы t элементі 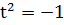шартын қанағаттандырады. Шынымен де, (V) және (ІІ) формулаларға байланысты бізде бар:

t*t=(0+1*t)(0+1*t)=-1+0*t=-1.

Сонымен, (2)-ге байланысты F алатіңы K өрістің өрісшесі болып табылады. Сәйкесінше, K өрісі F өрістің кешенді кеңейтілімі болып табылады.

ТЕОРЕМА.7,4 F=(F, +, -, *. 1) әрбір элементтің квадраты -1-ден ерекше өріс болсын. K мен K ` - F өрістің кешенді кеңейтілімдері болсын. Онда K `өрістегі K алаңының изоморфизмі болады, ол F өрістің барлық элменттерін өзгертусіз қалдырады.

Дәлелдеу. K -даu элементі бар, ол 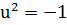және K өрістің барлық элементтері жалғыз түрде берілген a+bu,мұндағы a,b 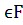. Сәйкесінше, K ' –да t элементі бар, ол t²=-1 және K ' өрістегіжалғыз түрде берілген a+bt, мұндағы a,b 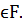К-ның К'-тегі көрсетілімін 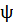арқылы белгілейік, K үшін a+buжәне К' үшін a+bt элементі қойылады. Сонымен қатар, ψ K өрістің барлық басты операцияларын сақтап қалады. Шынымен де, себебі:

(a+bu)+(c+du)=(a+c)+(b+d)u,

-(a+bu)=(-a)+(-b)u;

(a+bu)(c+du)=(ac-bd)+(ad+bc)u,

Немесе

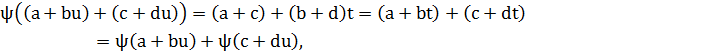
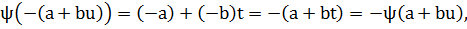
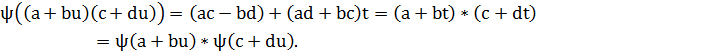
Сонымен қатар, F өрістің кез келген а бөлшегі үшін 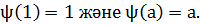Осылайша ψ К алаңының К' алаңындағы изоморфтық бейнесі болып табылады, ол F өрістің барлық бөлшектерін өзгертусіз қалдырады.

Кешенді сандар өрісі.Реттелген өрісте кез келген нолдік емес бөлшектің квадраты оң. Сәйкесінше, нақты сандар өрістегі кез келген нақты санның квадраты -1-ден ерекше. 7.3. теоремаға байланысты нақты сандардың кешенді кеңейтілімі R бар. 7.4. теорема бойынша R нақты сандар өрістің кез келген екі кешенді кеңейтілімі изоморфты.

АНЫҚТАМА. Кешенді сандар өрісі деп нақты сандар өрісінің кешенді кеңейтілімі аталады.

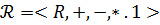- нақты сандар өрісі болсын. 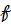– кешенді сандар өрісі, өрістің кешенді кеңейтілімі 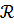өрісі болсын. Негізгі алаңының жиынтығын 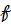арқылы 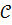белгілейік. С жиынтығының элементтері кешенді сандар деп аталады. іарқылы кешенді санды осылай белгілейік, ол 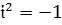және С-дағы кез келген кешенді сан z түрінде бере алатындай z=a+bi, мұндағы a, b 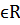. Бұл көрсетілім z санының алгебралық формасы деп аталады. .

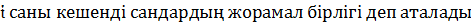ТЕОРЕМА.7,5 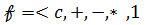–кешенді сандар өрісі, Rнақты сандар өрістің кешенді кеңейтілімі, u a , b , c , d - кез келген нақты сандар болсын. Онда

(1) a+bi=c+di сонда тек сондағана, сонда a=c және b=d;

(2) (a+bi)+(c+di)=(a+c)+(b+d)i;

(3) -(a+bi)=(-a)+(-b)I;

(4) (a+bi)(c+di)=(ac-bd)(ad+bc)i

(5) Егер a+bi 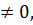онда (a+bi)^-1=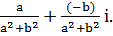

Дәлелдеу. a+bi=c+di болсын. Егер b=d , онда a=c . Егер b 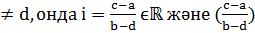²=-1, ол мүмкін емес. Сәйкесінше, b 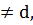болатын жағдай мүмкін емес. алаң болғандықтан, (2), (3) және (4) теңдіктер орынды.

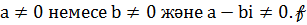a+bi болсын. Байланысты (1) өрістің кез келген екі нолдік емес бөлшектерінің туындысы нөлден ерекше болғандықтан, онда (a+bi)(a-bi)= .

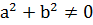Сәйкесінше: (a+bi)^-1=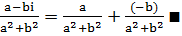

АНЫҚТАМА.Сандық өріс деп кешенді сандардың кез келген өрісшесі болып табылады.

Кез келген сандық алаңның рационалды сандар өрісшесі бар. Шынымен де F=<F, +, -, *, 1> - кез келген сандық өріс болсын. Себебі 0, 1 және F жиынтығы + , - , немесе n=1+…+1 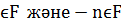операцияларына қатысты тұйық. Сәйкесінше F барлық бүтін сандарға ие. F жиынтығы бөлуге қатысты тұйық, яғни mn^-1 белгісімен бейнеленетін m/nтүріндегі барлық елементтерден тұрады. Сәйкесінше, F барлық рационалды сандардың Q жиынтығына ие. Q жиынтығы F алаңының басты операцияларына қатысты тұйық және Q-дағы кез келген нолдік емес элементтер кері қайтарымға ие. Яғни, 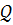алгебрасы, Q=<Q , + , - , * , 1>, F өрістің өрісшесі болып табылады. Сәйкесінше, F сандық алаңы Q рационалды сандар алаңшасынан тұрады.

АНЫҚТАМА. Сандық шеңбер деп кешенді сандар өрістің кез келген шеңбершесі аталады.

Осылайша, мысалы, 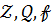шеңберлері сандық болып табылады. 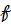алаңының шеңбершесі і элементінен туындап, 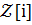белгіленеді және сандық өрісі болып табылады.

Байланыстырылған кешенді сандар.Егер z=a+bi болса, мұндағы a , b 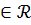, онда a – bi саны z арқылы белгіленеді.

АНЫҚТАМА. Kешенді сандар z=a+biжәне z=a-bi байланыстырылған деп аталады.

Алаңның өзінің изоморфтық бейнесі өрісінің автоморфизмі деп аталатынын еске салып өтейік.

ТЕОРЕМА.7,6 Егер z және z' – кез келген кешенді сандар болса, онда:

(1)

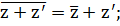
(2)

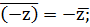
(3) 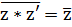*z’;

(4)

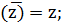
(5) z= сонда тек сонда ғана, сонда z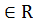

(6) егер z=a+bi, сонда z = .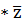

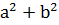САЛДАР.7,7 Кез келген кешенді сан z–ке байланыстырылған z' санын тудыратын кешенді сандар өрісінің өз бейнесі өрісінің автоморфизмі болып табылады, ол шынайы сандарды өзгертусіз қалдырады.

Кешенді сан модулі.

АНЫҚТАМА. Кешенді сан модулі a+bi (a , b 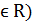деп санының арифтеикалық квадраттық түбірі болып a²+b² табылады, яғни (a²+b²)^1/2 саны. кешенді санының модулі z=a+bi арқылы |z| немесе |a+bi| арқылы белгіленеді. Осылайша, анықтамаға сәйкес; |z|²=a²+b².

ТЕОРЕМА 7.8. Кез келген кешенді сан үшін z және u

(1) |z|²=z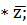

(2) |z|=0 сонда тек сонда ғана, сонда z=0;

(3) |zu|=|z|*|u|;

(4) |z^-1||z|^-1сонда z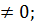

(5) |z+u|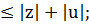

(6) |z|-|u| 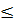|z+u|;

(7) ||z|-|u||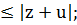

Дәлелдеу. (1) егер z=a+bi, сонда 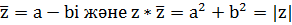²

(2) Егер |z|=|a+bi|=0, сонда |z|²=a²+b²=0. Себебі a, b нақты сан, яғни a²+b²=0 келесі a=b=0, t.e. z=0.

(3) Байланысты (1)

|zu|²=(zu)( 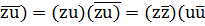)=|z|²|u|²=(|z|*|u|)².

Теңдеуден келесі формула шығады |zu|²=(|z|*|u|)² (3).

(4) (3) келісе , z 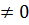болғанда

|z*z^-1|=|z|*|z^-1|=1.

Осыдан келе, |z^-1|=|z|^-1

(5) (1) негізге ала отырып

|z+1|²=(z+1)*( 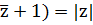²+z+ +1.

Сонымен қатар, егер z=a+bi, сонда z+ =2a 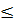2(a²+b²)^1/2=2|z|. сондықтан |z+1|² 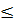(|z|+1)²; осыны негізге ала отырып, |z+1|≤|z|+1. (3) формуланы негізге ала отырып және сонғы теңсіздікті қосамыз, сонда u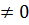

|z+u|=|u(zu^-1+1)|=|u||zu^-1+1| 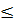|u|(|zu^-1|+1)=|u|(|z||u|^-1+1).

Осыны негізге ала отырып, |z+u|≤|z|+|u|.

(6) Сол сияқты z=-u+(z+u) және |-u|=|u|, байланысты

(5)|z|≤|-u|+|z+u|=|u|+|z+u|. осыны негізге ала отырып,

|z|-|u|≤|z+u|

1)

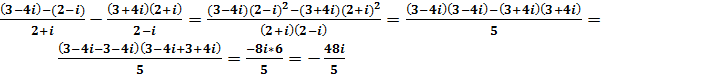
2) ;

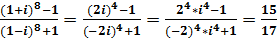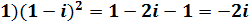
2)

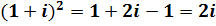
Қортынды:

Осыған дейін біздер нақты сандар жиынын қарастырып келдік. Нақты сандар жиынында сызықтық теңдеулердің және дискриминанты теріс емес квадрат теңдеулердің әр уақытта шешімдері бар. Ал дискриминанты теріс болатын квадрат теңдеулердің нақты сандар жиынында шешімдері жоқ. Мысалы, 2х+1=0 және 2х-4х+5=0 сияқты теңдеулердің нақты шешімдері болмайтынын жақсы білеміз. Сондықтан осындай теңдеулердің шешімдері бар болатындай етіп нақты сандар жиынын кеңейту қажеттігі туындайды. Мұндай тәсілдермен біз жақсы таныспыз. Мысалы, х+а=в, (а,в∈N) натурал сандар жиынында шешу мүмкіндігі бола бермегендіктен, нөл және теріс бүтін сандарды енгізіп, натурал сандар жиынын бүтін сандар жиынына дейін кеңейттік. Ал бүтін сандар жиынында ах=в теңдеуінің шешімі бола бермейтіндіктен, бөлшек сандар ұғымын енгізіп, рационал сандар жиынын анықтадық. Ең соныңда, 2х-2=0 теңдеуін қарастыра отырып, оның рационал шешімі болмайтынын көрсеттік те, иррационал сан ұғымын енгізіп, рационал сандар жиынын нақты сандар жиынына дейін кеңейттік. Сонымен, біз N – натурал сандар жиыны, Z-бүтін сандар жиыны, Q-рационал сандар жиыны, R-нақты сандар жиыны ұғымдарын енгізіп, олар үшін мынадай қатынастар орындалатынын көрсеттік. N Z Q R Осы сияқты, кез келген квадрат теңдеудің түбірлері болатындай етіп, нақты сандар жиынын кеңейту қажеттігі туындайды.Алдымен 2х+1=0 теңдеуін қарастырайық. Бұл теңдеудің нақты сандар жиынында түбірлері жоқ. Өйткені квадраты -1- ге тең болатын нақты сан табылмайды. Сондықтан квадраты -1-ге тең болатын жаңа сан ұғымын енгізу қажет. Осы жаңа санды i арқылы белгілейік.Сонда i2=-1 теңдігі орындалады деп есептейміз. i санын жорамал бірлік сан деп атаймыз. Осыдан 2х+1=0 , яғни 2х=-1 теңдеуінің 1х=i, 2х=-i болатынын көреміз. Жалпы, көп жағдайларда i2=-1 болғандықтан, i санын i=-1 теңдігімен анықтайды. Бұл анықтама математикалық тұрғыдан қарағанда дұрыс емес. Өйткені, √ белгісін арифметикалық квадрат түбір ретінде анықтадық және бұл түбір белгісі тек теріс емес сандарға ғана қолданылып, оның мәні теріс емес болды. Сондықтан осы айтылған түсінік тұрғысынан -1 өрнегінің мағынасы жоқ. Екінші жағынан, i=-1 теңдігі есептер шығару үшін өте қолайлы. Олай болса, -1 өрнегіне, яғни түбір белгісін бұрынғы анықтамасы бойынша қабылдамай, оған жаңа мағына беру қажет. Егер а>0 болса, онда -а өрнегін былай түсіну керек: -а=а i. Енді комплекс сандарға анықтама берейік. Анықтама. Егер а және в нақты сандар болса, онда а+вi өрнегін комплекс сан (жорамал сан) деп атайды. Мұнда а- комплекс санның нақты бөлігі деп, ал вi – жорамал бөлігі деп аталады. Оларды былай белгілейді: a=Rea+bi, b=Ima+bi. Комплекс сандарға амалдар қолдану.1.Егер екі комплекс сандардың нақты бөлігі мен нақты бөлігі, жорамал бөлігі мен жорамал бөлігі тең болса, онда бұл комплекс сандарды өзара тең деп атаймыз, яғни егер z=a+bi, w=c+di комплекс сандары үшін a=c, b=d теңдіктері орындалса, онда z және w комплекс сандарын өзара тең деп есептейміз және оны былай белгілейді: z=w .2. z=a+bi және w=c+di комплекс сандардың қосындысы деп a+c+(b+d)i комплекс санын айтады, яғни z+w=a+ib+c+id=a+c+ib+d. Сонымен, екі комплекс сандарды қосу үшін олардың нақты бөлігі мен нақты бөлігін, жорамал бқлігі мен жорамал бөлігін қосса, жеткілікті.Комплекс сандарды азайту z-w=a+ib-c+id=a-c+i(b-d)

z=a+bi және w=c+di комплекс сандарының көбейтіндісі депac-bd+i(ad+bc) түріндегі комплекс санды айтады, яғни z∙w=a+ib∙c+id=ac-bd+i(ad+bc) . Осыдан екі комплекс санды көбейтуді көпмүшені көпмүшеге көбейту ережесімен орындап, i2=-1 теңдігін ескерсе, жеткілікті болады.z=a+ib және z=a-ib түріндегі комплекс сандарын өзара түйіндес комплекс сандар деп аталады. Түйіндес комплекс сандардың көбейтіндісі нақты сан болады.Егер екі комплекс санның нақты бөліктерінің де, жорамал бөліктерінің де таңбалары қарама-қарсы болса, онда оларды қарама-қарсы комплекс сандар деп атайды. Қарама-қарсы комплекс сандардың қосындысы 0-ге тең. z=a+ib комплекс саны үшін a2+b2 теріс емес санын оның модулі деп атайды және модульді z арқылы белгілейді, яғни z =a2+b2 . Осыдан әрбір z комплекс саны мен оның түйіндесі z үшін z∙z=z2 теңдігі орындалатынын көреміз. Комплекс сандарды бір-біріне бөлу амалын көбейту амалына келтіріп орындайды:zw=a+ibc+id=ac+bd+i(bc-ad)c2+d2 =ac+bdc2+d2+bc-adc2+d2i

Пайдаланылған әдебиеттер:

1. Л.Я. Куликов « Алгебра и теория чисел»

2. А.И. Кострикин «Введение в алгебру»

3. А.Г. Курош «Курс высшей алгебра»