І. Елементи лінійної алгебри
1.1. Розв’язування систем лінійних алгебраїчних рівнянь методом Гаусса[1]
Розглянемо систему лінійних рівнянь(скорочено СЛР):
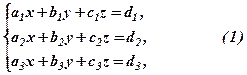
де 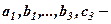 задані коефіцієнти,
задані коефіцієнти, 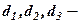 задані вільні члени,
задані вільні члени, 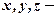 невідомі. В загальному випадку кількість рівнянь і невідомих може бути більшою. Коефіцієнти та вільні члени рівняння будемо називати його елементами.
невідомі. В загальному випадку кількість рівнянь і невідомих може бути більшою. Коефіцієнти та вільні члени рівняння будемо називати його елементами.
Множина чисел 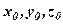 називається розв’язкомСЛР(1), якщо при підстановці
називається розв’язкомСЛР(1), якщо при підстановці 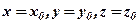 в СЛР(1) отримаємо числові тотожності.
в СЛР(1) отримаємо числові тотожності.
Наперед зауважимо, що СЛР(1) в залежності від її елементів може мати : 1)єдиний розв’язок; 2) безліч розв’язків; 3)зовсім не мати розв’язку.
У перших двох випадках СЛР називається сумісною , в третьому випадку — система несумісна .
Одним з широко відомих методів розв’язання СЛР є метод Гаусса, який полягає в послідовному виключенні невідомих шляхом елементарних перетворень. До елементарних перетворень СЛР будемо відносити:
1) переміну місцями рівнянь системи;
2) почленне множення обох частин одного з рівнянь на відмінне від нуля число;
3) додавання до обох частин одного з рівнянь відповідних частин іншого рівняння.
Нижче наводимо виклад методу Гаусса з використанням відомого в лінійному програмуванні правила прямокутника, але без ділення на провідний елемент. Останнє стає особливо зручним, коли коефіцієнти СЛР цілі і не дуже великі. В цьому випадку майже весь час оперуємо з цілими числами і результат, таким чином, отримуємо точний: у вигляді звичайних дробів, крім того, економиться час в процесі розв’язання. Все це дає можливість на практичних заняттях розглянути більше прикладів на дослідження СЛР та знаходження їх розв’язків.
Означення. Дві системи лінійних рівнянь називаються еквівалентними , якщо множини їх розв’язків збігаються. Якщо ж дві системи лінійних рівнянь несумісні, то вони теж вважаються еквівалентними.
Можна довести теорему:
Теорема. Внаслідок елементарних перетворень даної СЛР отримуємо систему еквівалентну даній.
Почнемо розв’язання СЛР(1) з виключення, наприклад, невідомого 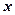 в другому, а тоді і в третьому рівняннях (скорочено будемо писати Р1 , P2 ). Для цього домножимо Р1 системи (1) на (
в другому, а тоді і в третьому рівняннях (скорочено будемо писати Р1 , P2 ). Для цього домножимо Р1 системи (1) на ( 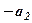 ), а Р2 на
), а Р2 на 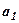 , після чого додамо відповідні частини цих рівнянь. Результат цих елементарних перетворень матиме вигляд:
, після чого додамо відповідні частини цих рівнянь. Результат цих елементарних перетворень матиме вигляд:
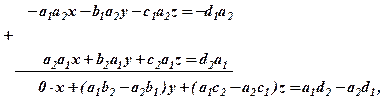
або, позначивши
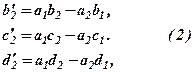
запишемо нове рівняння:
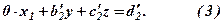
Отже, в другому рівнянні ми виключили невідоме 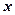 , тобто коефіцієнт при
, тобто коефіцієнт при 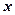 став рівним нулю.
став рівним нулю.
Здійснене перетворення, в результаті якого отримані нові значення елементів 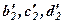 в (3) можна виразити за допомогою так званого правила прямокутника. Щоб його сформулювати випишемо у вигляді матриці (таблиці) елементи першого і другого рівнянь.
в (3) можна виразити за допомогою так званого правила прямокутника. Щоб його сформулювати випишемо у вигляді матриці (таблиці) елементи першого і другого рівнянь.
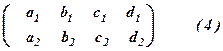
Умовно можна розглянути прямокутник, у вершинах якого розміщені елементи 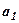 ,
, 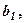
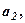
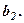 Назвемо елемент
Назвемо елемент 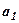 (обведений рамкою) – провідним ,
(обведений рамкою) – провідним , 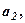
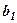 (обведені кружочками) – супутними елементами,
(обведені кружочками) – супутними елементами, 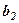 (обведений трикутником) – старим перетворюванимелементом, а значення
(обведений трикутником) – старим перетворюванимелементом, а значення 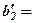
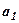
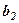 –
– 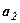
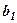 назвемо новим перетворенимелементом — це коефіцієнт при
назвемо новим перетворенимелементом — це коефіцієнт при 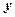 в (3).
в (3).
Правило прямокутника. Новий перетворений елемент дорівнює різниці між добутком провідного елемента на старий перетворюваний елемент та добутком супутних елементів.
 Як бачимо всі співвідношення (2) можна отримати із (4) за правилом прямокутника:
Як бачимо всі співвідношення (2) можна отримати із (4) за правилом прямокутника: 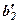 із прямокутника
із прямокутника


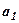
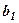


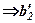 =
= 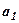
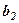 –
– 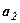
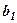 ,
,
 |


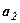
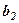
 |
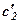 із прямокутника
із прямокутника



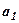
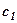
 |  | ||


 Þ
Þ 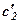 =
= 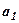
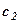 –
– 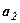
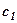 ,
,

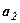
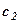
 |
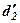 із прямокутника
із прямокутника



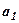
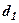
 | |||
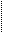 | |||

 Þ
Þ 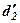 =
= 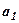
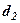 –
– 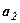
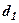 .
. 
 а2 d2
а2 d2

Це всі елементи рівняння (3). До речі, коефіцієнт при 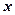 в (3) теж знаходиться за цим правилом прямокутника
в (3) теж знаходиться за цим правилом прямокутника



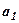
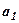


 Þ
Þ 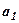
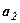 –
– 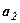
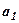 =
= 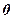 ,
,
 |

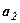
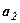
 |
в якого дві сторони (два стовпці) однакові. Таким чином, виходячи з матриці (таблиці) (4) ми отримуємо систему прямокутників, в кожному з яких ліва сторона (лівий стовпець матриці (4)) одна і та ж, а права сторона по черзі займає положення другого, третього та четвертого стовпців.
Застосування встановленого правила для кожного з прямокутників дає можливість записати рівняння (3) без детального виконання елементарних перетворень.
Тепер виключимо невідоме 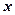 із третього рівняння, застосовуючи викладену вище ідею, тобто за правилом прямокутника без виконання елементарних перетворень. Запишемо елементи першого і третього рівнянь у вигляді матриці
із третього рівняння, застосовуючи викладену вище ідею, тобто за правилом прямокутника без виконання елементарних перетворень. Запишемо елементи першого і третього рівнянь у вигляді матриці
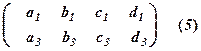
з провідним елементом 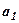 , тоді
, тоді
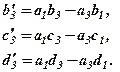
Після цього третє рівняння матиме вигляд
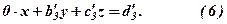
Запишемо нову систему
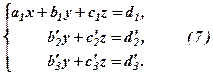
СЛР (7) є еквівалентною системі (1), але останні два рівняння містять тільки двоє невідомих . Вважаючи, що 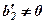 , виберемо його провідним елементом і виключимо
, виберемо його провідним елементом і виключимо 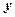 в третьому рівнянні вже за відомим правилом. Запишемо матрицю:
в третьому рівнянні вже за відомим правилом. Запишемо матрицю:
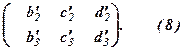
Позначивши 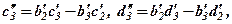 в результаті виключення
в результаті виключення 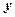 із третього рівняння системи (7) отримуємо:
із третього рівняння системи (7) отримуємо:
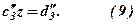
Враховуючи (9) складаємо нову систему:
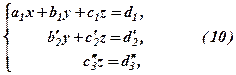
яка еквівалентна СЛР(7), а, значить, і СЛР(1). Таким чином, систему (1) ми звели до еквівалентної, що має трикутну форму, системи (10), яка вже розв’язується легко. Знаходження 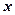 ,
, 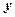 ,
, 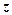 із СЛР(10) називається зворотним ходом. Розкриємо його зміст.
із СЛР(10) називається зворотним ходом. Розкриємо його зміст.
Нехай в СЛР(10) 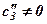 , тоді із третього рівняння (скорочено Р3) знаходимо:
, тоді із третього рівняння (скорочено Р3) знаходимо:
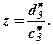
Позначимо  Із Р2 СЛР(10) при
Із Р2 СЛР(10) при 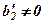 маємо
маємо
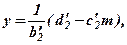
або, позначивши через 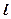 значення останнього виразу, запишемо
значення останнього виразу, запишемо 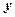 =
= 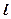 . Нарешті, із Р1 знаходимо:
. Нарешті, із Р1 знаходимо:
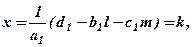
де 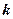 – теж позначення останнього виразу. Таким чином, знайшли
– теж позначення останнього виразу. Таким чином, знайшли
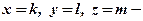 розв’язок СЛР(10), а, значить, і початкової системи (1).
розв’язок СЛР(10), а, значить, і початкової системи (1).
На практиці розв’язання систем лінійних рівнянь зручно вести за допомогою обчислювальної таблиці 1:
Таблиця 1
| № п/п | Коефіцієнти при | Вільні члени | Суми | Контроль | ||
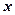 | 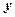 | 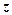 | ||||
    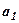 | 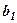 | 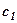 | 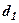 | 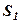 | ||
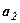 | 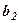 | 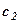 | 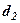 | 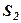 | ||
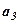 |  | 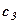 | 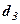 | 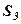 | ||
   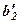 | 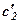 | 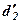 | 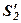 | 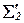 | ||
 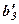 |    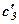 | 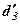 |  | 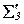 | ||
 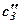 | 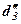 | 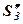 | 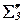 |
В таблиці 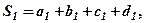
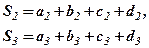 – це суми елементів відповідних рівнянь. В рядках 4 і 5 елементи перетворених за правилом прямокутника другого і третього рівнянь системи (1), а
– це суми елементів відповідних рівнянь. В рядках 4 і 5 елементи перетворених за правилом прямокутника другого і третього рівнянь системи (1), а
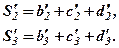
В шостому рядку елементи перетвореного третього рівняння
системи (7), а
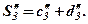
У стовпчику “контроль” записані результати перетворень за правилом прямокутника значень сум 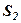 і
і 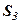 , тобто
, тобто
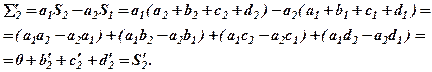 Аналогічно
Аналогічно 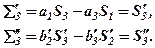
Те, що суми 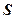 і
і 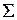 у стовпчиках 5 і 6 збігаються свідчить про вірність поточних результатів обчислень.
у стовпчиках 5 і 6 збігаються свідчить про вірність поточних результатів обчислень.
Після заповнення всіх рядків 1-6 таблиці на основі даних в рядках 1, 4, 6 записуємо трикутну систему (10), з якої тоді починається зворотний хід.
