Модуль 2 Элементы теории поля
2.1.В каждой точке поверхности 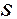 , лежащей в первом октанте, уравнение которой
, лежащей в первом октанте, уравнение которой 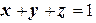 , распределена масса с плотностью
, распределена масса с плотностью 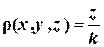 , где
, где 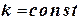 . Вычислить массу пластинки.
. Вычислить массу пластинки.
Решение. Масса вычисляется по формуле 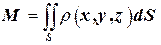 . Имеем:
. Имеем:
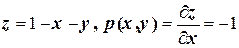 ,
, 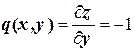 ,
,
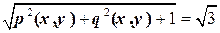 .
.
Следовательно, масса 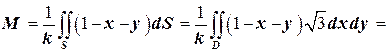
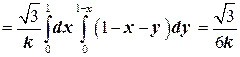 кв. ед.
кв. ед.
2.2.Вычислить 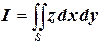 по нижней стороне поверхности
по нижней стороне поверхности 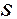 , заданной уравнением
, заданной уравнением 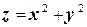 над областью
над областью 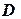 , ограниченной прямыми
, ограниченной прямыми 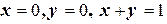 .
.
Решение.
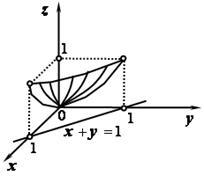 | В соответствии с теоремой существования и принимая во внимание, что поверхностный интеграл берётся по нижней стороне поверхности 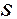 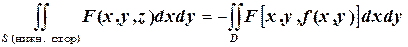 , получим , получим 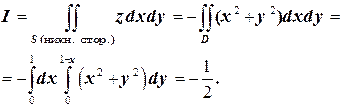 |
2.3. С помощью формулы Остроградского вычислить интеграл 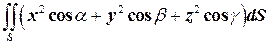 , где
, где 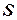 – часть конической поверхности
– часть конической поверхности 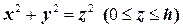 , а
, а 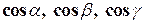 – направляющие косинусы внешней нормали к поверхности.
– направляющие косинусы внешней нормали к поверхности.
Решение. Формула Остроградского применима в случае замкнутой поверхности.
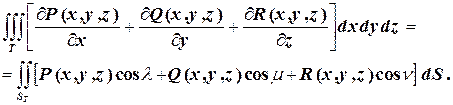
Чтобы получить замкнутую поверхность, присоединим к поверхности конуса соответствующую часть плоскости 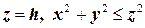 . Обозначив эту часть плоскости через
. Обозначив эту часть плоскости через 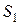 , по формуле Остроградского получаем:
, по формуле Остроградского получаем:
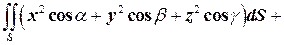
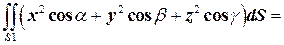
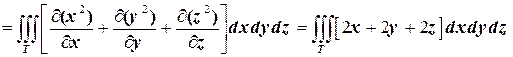 .
.
Таким образом,
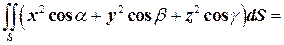 -
- 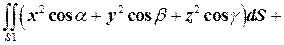
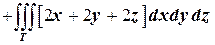 .
.
Для решения задачи необходимо вычислить интегралы, стоящие в правой части. В случае области 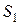
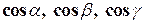 – косинусы углов с осями координат нормали к плоскости
– косинусы углов с осями координат нормали к плоскости 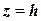 , а именно:
, а именно: 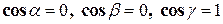 . Поэтому
. Поэтому
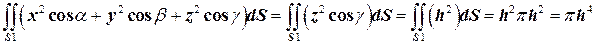 ,
,
Так как на плоскости 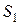
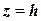 и двойной интеграл равен площади круга радиуса
и двойной интеграл равен площади круга радиуса 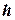 , получающегося при пересечении конуса плоскостью.
, получающегося при пересечении конуса плоскостью.
При вычислении интеграла по объему 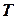 производим сначала интегрирование по
производим сначала интегрирование по 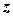 от
от 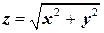 до
до 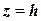 . Затем двойной интеграл по области
. Затем двойной интеграл по области 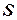 в плоскости
в плоскости 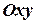 . Эта область является кругом
. Эта область является кругом 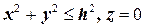 . Она получается проецированием объема
. Она получается проецированием объема 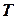 на плоскость
на плоскость 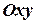 .
.
Таким образом,
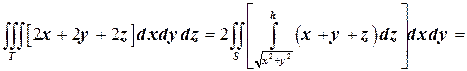
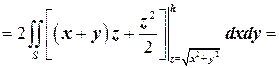
 .
.
Обозначая последний интеграл через 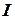 и переходя к полярным координатам по формулам
и переходя к полярным координатам по формулам
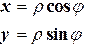 ,
,
находим
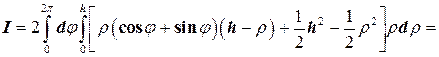
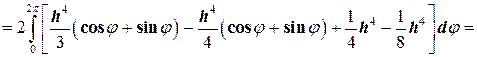
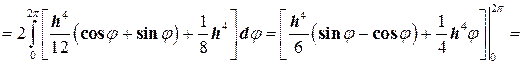
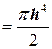 .
.
Итак, 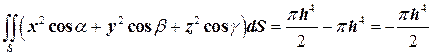 .
.
2.4.Вычислить поверхностный интеграл 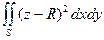 по верхней стороне полусферы
по верхней стороне полусферы
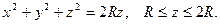
Решение: Преобразуем уравнение поверхности к виду: 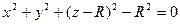
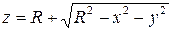
Заданная поверхность проецируется на плоскость XOY в круг, уравнение которого:
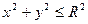
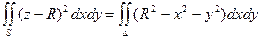
Для вычисления двойного интеграла перейдем к полярным координатам:
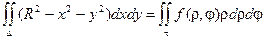 ,
, 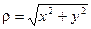
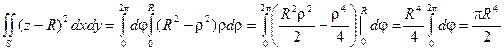
2.5 Найти объем шара 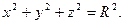
Решение: Найти объем шара можно по формуле:
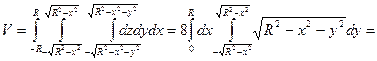
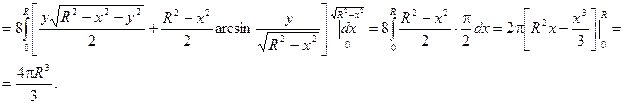
2.6. С помощью формулы Стокса вычислить криволинейный интеграл
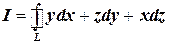 , где
, где 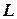 – окружность
– окружность 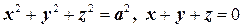 , пробегаемая против часовой стрелки, если смотреть с положительной стороны оси
, пробегаемая против часовой стрелки, если смотреть с положительной стороны оси 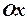 .
.
Решение.
В нашем случае 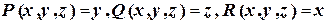 , поэтому
, поэтому 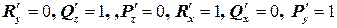 .
.
По формуле
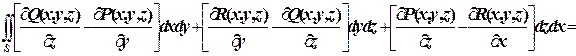 |
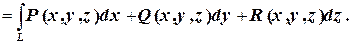 |
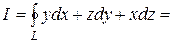
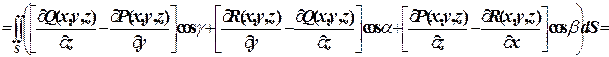
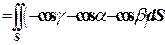 , где
, где 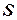 – часть плоскости
– часть плоскости 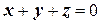 , ограниченная окружностью. Приводя уравнение окружности к нормальному виду, находим
, ограниченная окружностью. Приводя уравнение окружности к нормальному виду, находим
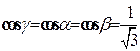 .
.
Таким образом, 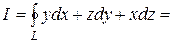
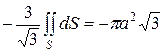 , где
, где 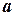 – радиус круга, ограниченного указанной окружностью.
– радиус круга, ограниченного указанной окружностью.
2.7. Найти частные производные функции 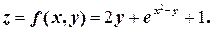
Решение.
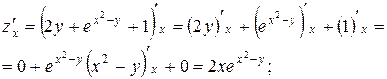
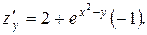
2.8.Найти частные производные второго порядка функции 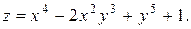
Решение. Так как 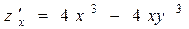 и
и 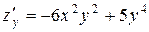 , то
, то 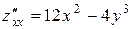 и
и 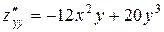 . Смешанные производные
. Смешанные производные 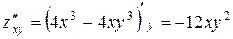 и
и 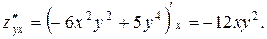
2.9. Найти производную скалярного поля 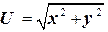 по направлению кривой
по направлению кривой 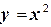 от точки
от точки 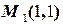 к точке
к точке 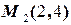 в точке
в точке 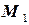 .
.
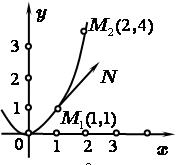 | Решение. Найдём единичный вектор 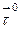 , касательный к параболе , касательный к параболе 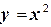 в точке в точке 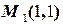 . (рис.32). Найдём угловой коэффициент прямой, на которой лежит вектор . (рис.32). Найдём угловой коэффициент прямой, на которой лежит вектор 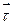 : : 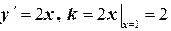 . Прямая имеет угловой коэффициент . Прямая имеет угловой коэффициент 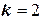 и проходит через точку и проходит через точку 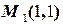 , следовательно, её уравнение , следовательно, её уравнение 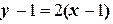 . . |
Запишем это уравнение в каноническом виде: 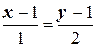 . Вектор
. Вектор 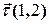 - направляющий вектор этой прямой, причём его направление соответствует направление на кривой от точки
- направляющий вектор этой прямой, причём его направление соответствует направление на кривой от точки 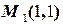 к точке
к точке 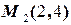 . Соответствующий ему единичный вектор
. Соответствующий ему единичный вектор 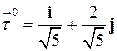 , т.е. его направляющие косинусы
, т.е. его направляющие косинусы 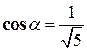 ,
, 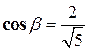 .
.
Найдём теперь 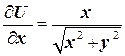 ,
, 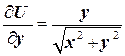 , а тогда производная по направлению функции
, а тогда производная по направлению функции 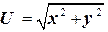 в точке
в точке 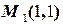 по кривой
по кривой 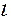 от точки
от точки 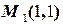 к точке
к точке 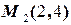 будет
будет
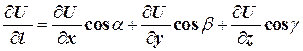 ,
,
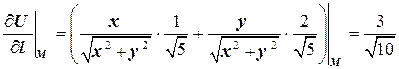 .
.
2.10.Найти дивергенцию векторного поля
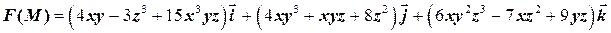 в точке
в точке 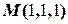 .
.
Решение. Вычислим частные производные 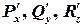 в точке
в точке 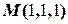 .
.
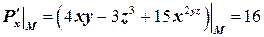 ,
,
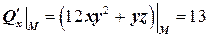 ,
,
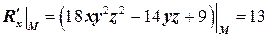 .
.
Подставляя полученные значения в формулу
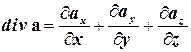 , получаем:
, получаем:
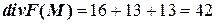 .
.
2.11. Найти поток векторного поля 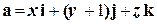 из тела, ограниченного координатными плоскостями
из тела, ограниченного координатными плоскостями 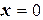 ,
, 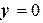 ,
, 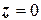 и плоскостью
и плоскостью 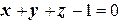 наружу по теореме Остроградского и непосредственно .
наружу по теореме Остроградского и непосредственно .
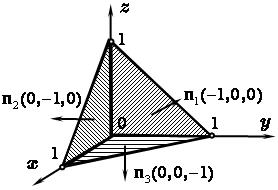 | Решение. 1-й метод решения. Вычислим поток векторного поля по теореме Остроградского. Найдём 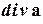 . Имеем: . Имеем: 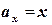 , , 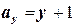 , , 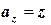 . Значит, . Значит, 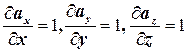 . Следовательно, . Следовательно, 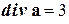 . . |
Поток векторного поля 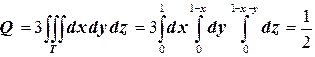 .
.
2-й метод решения. Вычислим поток векторного поля с помощью интеграла первого рода.
Имеем: 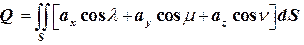 , где
, где 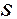 полная поверхность тела
полная поверхность тела 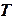 , состоящая из четырёх частей:
, состоящая из четырёх частей: 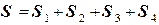 ; здесь
; здесь 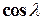 ,
, 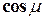 и
и 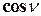 - направляющие косинусы внешней нормали к поверхности;
- направляющие косинусы внешней нормали к поверхности;
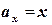 ,
, 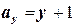 ,
, 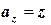 ;
;
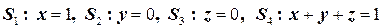 .
.
Поток 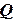 можно представить в виде суммы четырёх потоков:
можно представить в виде суммы четырёх потоков:
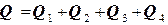 . Вычислим каждый из потоков:
. Вычислим каждый из потоков:
1. 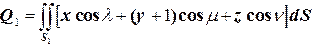 ,
, 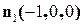 , т.е.
, т.е.
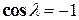 ,
, 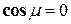 ,
, 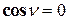 ,
, 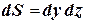 .
.
Следовательно, 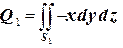 , т.к.
, т.к. 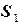 есть поверхность
есть поверхность 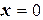 .
.
2. 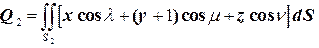 ,
, 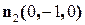 , т.е.
, т.е.
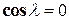 ,
, 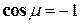 ,
, 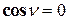 .
.
Таким образом: 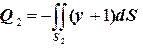 . Здесь
. Здесь 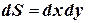 ,
, 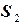 :
: 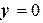 , следовательно,
, следовательно, 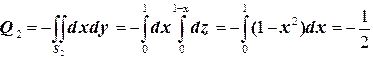 .
.
3. 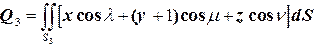 ,
, 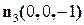 , т.е.
, т.е.
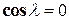 ,
, 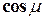 ,
, 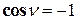 ,
,
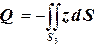 , т.к. на поверхности
, т.к. на поверхности 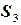
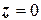 .
.
4. 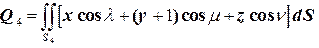 .
.
Поверхность 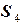 имеет уравнение
имеет уравнение 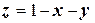 , следовательно,
, следовательно,
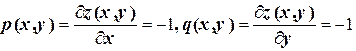 ,
,
тогда 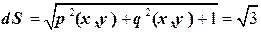 . Поверхностный интеграл здесь вычисляется по верхней стороне поверхности
. Поверхностный интеграл здесь вычисляется по верхней стороне поверхности 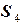 , значит направляющие косинусы нормали
, значит направляющие косинусы нормали 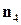 будут равны:
будут равны:
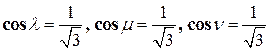 .
.
Тогда получим
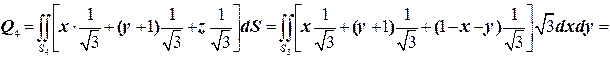
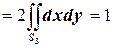 .
.
Окончательно: 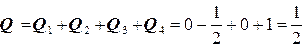 .
.
3-й метод решения. Вычислим тот же самый поток с помощью поверхностного интеграла второго рода 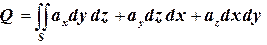 .
.
В нашем случае 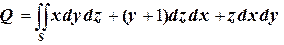 , как и в предыдущем случае, поток
, как и в предыдущем случае, поток 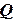 представим в виде суммы четырёх потоков соответственно, через поверхности
представим в виде суммы четырёх потоков соответственно, через поверхности 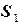 ,
, 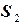 ,
, 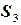 ,
, 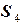 :
:
1. На 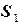
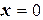 ,
, 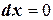 , а значит
, а значит 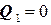 .
.
2. На 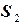
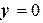 ,
, 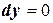 . Сторона поверхности, по которой вычисляется интеграл, нижняя. Нормаль к поверхности образует тупой угол с осью Ох. Значит
. Сторона поверхности, по которой вычисляется интеграл, нижняя. Нормаль к поверхности образует тупой угол с осью Ох. Значит
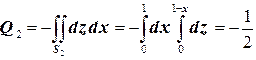
3. На 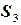
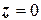 ,
, 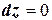 , сторона поверхности нижняя и
, сторона поверхности нижняя и 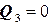 .
.
4. 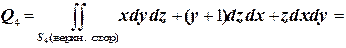
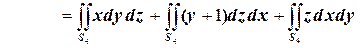 .
.
На 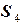
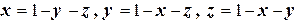 .
.
Следовательно,
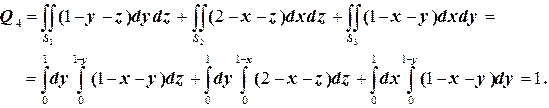
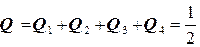 .
.
9.25 Найти ротор поля 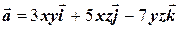 .
.
Решение.
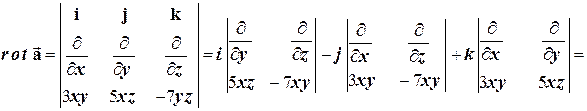
= 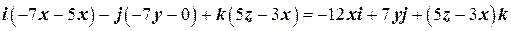 .
.
2.12. Вычислить циркуляцию векторного поля 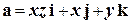
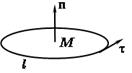 | по линии пересечения конуса 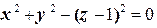 с координатными плоскостями, лежащей в первом октанте, непосредственно и по теореме Стокса с координатными плоскостями, лежащей в первом октанте, непосредственно и по теореме Стокса |
Решение.
1) Непосредственное вычисление циркуляции. Контур 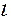 можно разбить на три части:
можно разбить на три части: 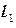 ,
, 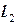 и
и 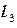 , лежащие в координатных плоскостях
, лежащие в координатных плоскостях 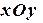 ,
, 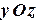 и
и 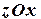 соответственно, таким образом циркуляция Ц=Ц1+Ц2+Ц3 , где
соответственно, таким образом циркуляция Ц=Ц1+Ц2+Ц3 , где
Ц1= 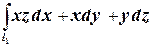 . На кривой
. На кривой 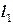 :
: 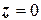 ,
, 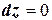
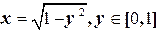 . Следовательно, Ц1=
. Следовательно, Ц1= 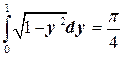 . Далее
. Далее
Ц2= 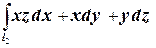 . На кривой
. На кривой 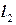 :
: 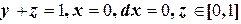 , т.е.
, т.е.
Ц2= 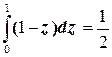 . И, наконец,
. И, наконец,
Ц3= 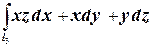 . На кривой
. На кривой 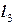 :
: 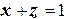 ,
, 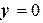 ,
, 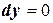 ,
, 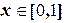 , следовательно, Ц3=
, следовательно, Ц3= 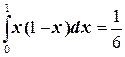 .
.
Окончательно Ц=Ц1+Ц2+Ц3 = 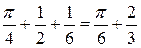 .
.
2) Вычисление циркуляции по теореме Стокса:
Ц= 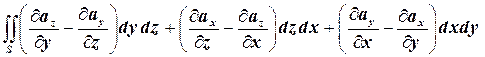 .
.
Подставим сюда 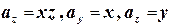 , получим
, получим
Ц1= 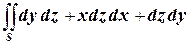 . Перейдём в правой части к поверхностному интегралу первого рода Ц=
. Перейдём в правой части к поверхностному интегралу первого рода Ц= 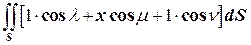 , где интеграл вычисляется по верхней стороне поверхности
, где интеграл вычисляется по верхней стороне поверхности 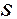 .
.
Уравнение поверхности 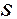 :
: 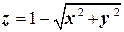 , следовательно,
, следовательно,
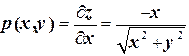 ,
, 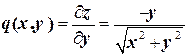 ,
, 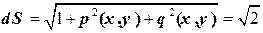 ;
;
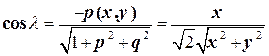 ;
; 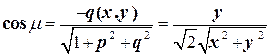 ;
; 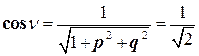 .
.
Подставляя найденные значения в выражение для циркуляции, получим
Ц= 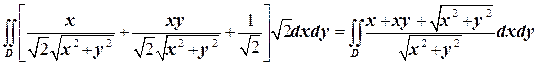 .
.
Перейдём к полярным координатам:
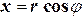 ,
, 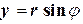 ,
, 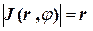 ,
,
тогда
Ц= 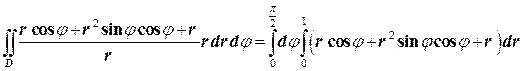 .
.
 Вычислим внутренний интеграл:
Вычислим внутренний интеграл: 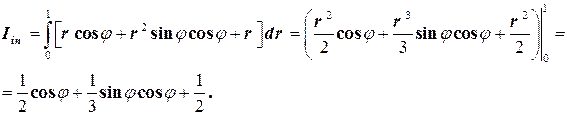
Тогда Ц= 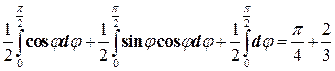 .
.
2.13Найти 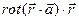 , если
, если 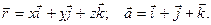
Решение: Найдем скалярное произведение: 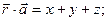
Найдем скалярное произведение:
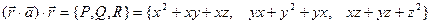
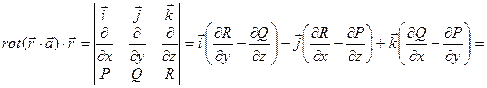
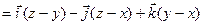
2.14Найти поток векторного поля 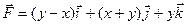 через сторону треугольника S, вырезанного из плоскости
через сторону треугольника S, вырезанного из плоскости 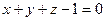 координатными плоскостями.
координатными плоскостями.
Решение:
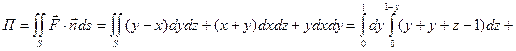
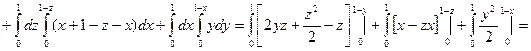
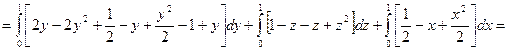
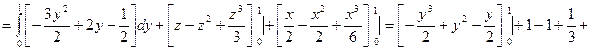
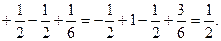
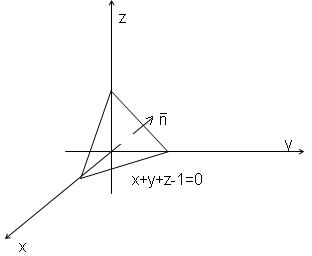
2.15Найти div(grad u), если 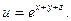
Решение: 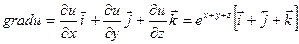
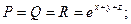
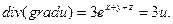
2.16Определить является ли векторное поле 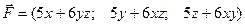
потенциальным и найти его потенциал.
Решение: 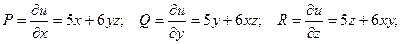
Если поле потенциально, то должны выполняться следующие условия:
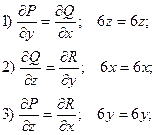
Эти условия эквивалентны условию равенства нулю ротора векторного поля, справедливость этого утверждения видна из формулы ротора.
Таким образом, поле потенциальное. Потенциал находится по формуле: