Порядок выполнения работы. 1. Измерить T2эфф в зависимости от раздвижки между импульсами при комнатной температуре

1. Измерить T_2эфф в зависимости от раздвижки между импульсами при комнатной температуре.

2. Построить спад поперечной намагниченности A(t) с помощью метода спинового эхо и использования импульсной последовательности 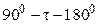при комнатной температуре. Определить время T₂ (время уменьшения A(t) в e раз от начального значения).

3. Повторить измерения п.п. 1 и 2 при температурах выше комнатной (30⁰ и 40⁰С).

4. Для каждой температуры построить график зависимости 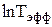от 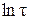и по тангенсу ее угла наклона найти параметр ширины спектра .

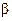5. Для каждой температуры построить график зависимости 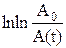от lnt и вычислить тангенс ее угла наклона, равный согласно (38а) 2–β. Найти величину β.

6. Построить график зависимости lnT_2эфф от обратной температуры 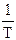при некотором фиксированном значении раздвижки 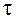. Из этого графика найти тангенс угла наклона 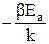и, взяв значение параметра β, найденного в п. 4, определить энергию активации E_a .

7. Построить график зависимости lnT₂ от обратной температуры 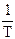, из которого найти тангенс угла наклона 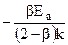и, взяв значение параметра β, найденного в п.5, определить энергию активации E_a.

Контрольные вопросы

1. С помощью каких функций принято описывать движение ядер, связанных диполь-дипольным взаимодействием?

2. Что такое функция корреляции (каков ее физический смысл)?

3. Что такое функция спектральной плотности (каков её физический смысл)?

4. Как связаны функция спектральной плотности с функцией корреляции?

5. Как времена релаксации Т₁ и Т₂ выражаются через функции спектральной плотности?

6. Какой вид имеет спад поперечной намагниченности A(t) при наличии экспоненциальной функции корреляции?

7. Как преобразуется форма спада поперечной намагниченности A(t) в случае быстрых и медленных движений?

8. Что представляет собой время корреляции?

9. Как время корреляции зависит от температуры?

10. Как рассчитывается энергию активации для молекулы?

11. Приведите примеры функций распределения времен корреляции.

12. Какие особенности в поведении времен релаксации Т₁, Т₂ и Т_2эфф и в функции спада поперечной намагниченности наблюдаются в случае распределения Фуосса–Кирквуда?

Литература

1. Ядерный магнитный резонанс: Учеб. пособие / Бородин П.М., Володичева М.И., Москалев В.В., Морозов А.А. и др.; Под ред. П.М. Бородина. Л.: Изд-во Ленингр. ун-та, 1982, 344 С.

2. Фаррар Т., Беккер Э. Импульсная и Фурье-спектроскопия ЯМР. М.: Мир, 1973, 166 С.

3. Вашман А. А., Пронин И.С. Ядерная магнитная релаксация и ее применение в химической физике. М.: Наука, 1979, 236 С.

4. Слоним И.Я., Любимов А.Н. Ядерный магнитный резонанс в полимерах. М.: Химия, 1967, 340 С.

5. Чернов В.М. Ядерная магнитная релаксация и форма спектра времен корреляции

в каучуках, в cб. Ядерный магнитный резонанс и динамика спиновых систем, Красноярск, 1988, С. 135-143.

6. Чернов В.М., Федотов В.Д. Ядерная магнитная релаксация и природа распределения времен корреляции сегментального движения в каучуках // Высокомолек. соединения. 1981. Т. 23 А, N 4, C. 932-942.

7. Рот Г.К. и др. Радиоспектроскопия полимеров: Пер. с нем. / Г.К. Рот, Ф. Келлер, Х. Шнайдер. М.: Мир, 1987, 380 С.

Лабораторная работа N3