Зіксіздік теңдеуі

Кез-келген анықталған жүйе үшін сұйықтық массасын сақтау принципі мынада:

жүйеге сұйықтық массасының таза құйылуы = жүйенің сұйықтық массасының өсімшесіне.

y

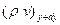
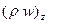
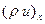
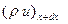
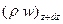
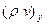
z x

3.2 сур. Үзіксіздік теңдеуің қорытуға арналған сұлба.

Кейбір ағыс аймағы ішінен, масса көздері (құйылыстары) жоқ, ал тығыздық пен жылдамдық уақыт пен кеңістік координаталарының функциясы болып табылатын (3.2 сур.), параллелепипед пішінді қарапайым бақылау көлемді 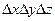қарастырайық. Осы көлемге таза масса құйылуын есептейік.

Анықтама бойынша, ағын массасы массалық жылдамдықтың жылдамдыққа нормаль болатын аудан қимасына көбейтіндісіне тең. Сонда қарастырып жатқан көлемге келесі сұйықтық мөлшері құйылады

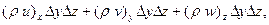
ал көлемнен ағылады .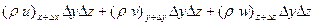

Сонымен, параллелепипед көлеміндегі сұйық массасының өзгеруі құрады:

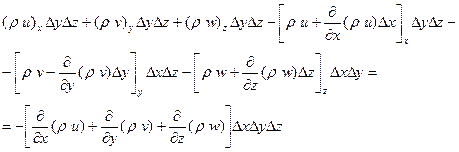(3.2)

Мұнда шығып жатқан масса ағынын сызықты қосылғыштар дәлдігімен Тейлор қатарына жіктеуі пайдаланылған.

Бөлінген көлемдегі сұйық массасының өсімшесі тең:

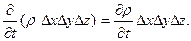(3.3)

Мұнда 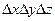уақытқа тәуелді емес, себебі бақылау көлемі қозғалмайды. (3.2) және (3.3) теңдеулерін теңестіре отырып, 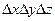-ке қысқартылғаннан кейін аламыз

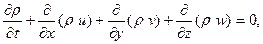(3.4)

немесе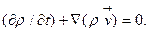

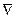операторын массалық жылдамдықтың векторына 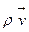көбейтіндісі скаляр шамасы болады, және жылдамдықтың дивергенциясы 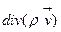деп аталады. Ол сұйықтықтың қарапайым (элементар) массасының салыстырмалы өзгерісінің жылдамдығын сипаттайды, яғни V көлемнің S беті арқылы өтетін сұйықтықтың массалық шығынының осы көлем шамасына, оны нөлге ұмтылғандағы қатынасына тең.

Көбейтінділердің дифференциалдау ережесін пайдаланып және мынаны ескере отырып:

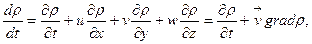
(3.4) теңдеуді мына түрде жазуға болады:

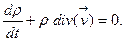(3.5)

Егер 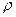уақытқа тәуелді болмаса, онда 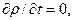және (3.4) теңдеуінің орнына аламыз

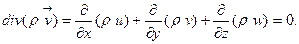(3.6)

Мұндай қозғалысты изохорлық деп атайды. Егер 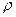координаталардан да тәуелсіз болса, онда 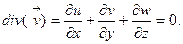(3.7)

Бұл сығылмайтын сұйықтықтың қалыптасқан және қалыптаспаған ағыстары үшін үзіксіздік теңдеуінің қарапайым түрі.

Сығылмайтын сұйықтықтың екіөлшемді ағысы үшін ток функциясы. Құйынды және құйынсыз қозғалыстар. Жылдамдық потенциалы.

Үзіксіздік теңдеудің төрт белгісізі бар екенін оңай байқауға болады: тығыздық 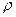және жылдамдықтың үш компоненттері (құрамалары) 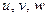. Ағынды сипаттау үшін бір үзіксіздік теңдеуі жеткіліксіз. Бірақта сұйықтық ағысы екіөлшемді ретінде қарастырылуы мүмкін жағдайда, үзіксіздік теңдеуі негізінде ток сызығының орналасуы мен ағыс өрісіндегі жылдамдықтардың үлестірімі арасындағы қызықты және пайдалы байланыс орнатылуы мүмкін.

Сығылмайтын сұйықтық жағдайымен шектелеміз. Жазық параллель ағыс үшін үзіксіздік теңдеуі мына түрге келеді.

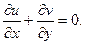(3.8)

Ток функциясын енгіземіз, жаза отырып

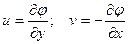. (3.9)

Сонда (3.8) теңдеуі тепе-тендік қанағаттандырылады, себебі

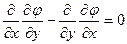. (3.10)

Жазық параллель ағыс үшін ток сызығы теңдеуі келесі түрге ие болады

.

(3.9) өрнегін пайдалана отырып ток сызығы бойында табамыз

.

Дифференциал 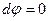болғандықтан, ток сызығы бойында .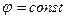