Лесотехнический институт им. В.В.Куйбышева

РСФСР

Архангельский ордена Трудового Красного Знамени

"Утверждаю"

Проректор по научной работе,

доцент____________ Т.А.Гурьев

" 25 " ______марта__ 1980 г.

М Е Х А Н И К А

Методические указания к выполнению

лабораторных работ

Архангельск

Рассмотрены и рекомендованы к изданию методической

комиссией химико-технологического факультета

Архангельского ордена Трудового Красного Знамени

лесотехнического институтаим. В.В.Куйбышева

6 октября 1978 г.

Составители:

С.П.АРТЮХОВ, В.В.НЕКРАСОВ, З.Г.ИВАЩЕНКО,

Ф.А.БОДНАРЮК, Л.Ф.ТРЕНИНА

Научный редактор

канд.хим.наук доцент Б.К.СЕМЕНОВ

Рецензент

ст. преп. И.Ф.П0ПОВА

УДК 531/534

Механика: Методические указания к выполнению лабораторных работ/ Артюхов С.П., Некрасов В.В., Иващенко З.Г., Боднарюк Ф.А., Тренина Л.Ф., -РИО АЛТИ, 1980,- 28 с. Подготовлены кафедрой фи­зики АЛТИ.

Методические указания включают описание шести лабораторных работ, связанных с изучением основных законов поступательного, вращательного и колебательного движений, а также механических законов сохранения, и отражают основные разделы читаемого курса. Первая цифра номера работы определяет номер части ("Механика и молекулярная физике"), вторая - номер цикла, третья - номер ла­бораторной работы в цикле. Методические указания предназначены для студентов I, II курсов всех факультетов и всех форм обучения.

Ил. 8 . Табл. 7. Библиогр. 2 назв.

© АЛТИ, 1980

КРАТКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ

Измерить какую-либо величину - это значит определить, сколько раз содержится в ней однородная величина, принятая за единицу измерения.

Измерения подразделяются на прямые и косвенные. При прямых измерениях определяемая величина сравнивается с единицей изме­рения непосредственноили с помощью измерительных приборов, прикосвенных - по результатам прямых измерений других величин, связанных с ней функциональной зависимостью.

Величины, полученные в результате лабораторных измерений, не являются точными, тек как в процессе измерений всегда допускаются ошибки, обусловленные несовершенством приборов, наших органов чувств и изменяющимися внешними условиями.

Результат любых измерений только тогда имеет смысл, когда проведена оценка степени точности намерений. В теории погреш­ностей для оценки степени точности и качества измерений исполь­зуют понятия абсолютной и относительной погрешностей.

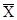Теория вероятности показывает, что среднее арифметическое очень большого числа n измерений, произведенных в одинако­вых условиях, какой-либо величины равно истинному значениюэтойвеличины Х.(Это справедливо при 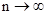.) Среднее арифмети­ческое из ограниченного числа измерений 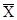как правило отлича­ется от Х истинного.

Одной из основных задач теории погрешностей является вы­числение интервала с центром в 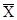и полушириной Δ Х , то есть интервала от 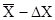до 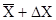, в который с заданной степенью вероятности должно попасть истинное значение измеряемой величи­ны. Такой интервал и соответствующую ему вероятность называютдоверительным. Величина 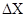, отмечающая границы доверительного интервала, называется абсолютной погрешностью. Абсолютная по­грешность - величина, имеющая ту же размерность, что и измеряе­мая величина.

Если 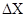равно так называемой среднеквадратичной ошибкеS_nтo доверительная вероятностьα,, соответствующая интервалу с полушириной S_n , равна примерно 2/3 (67%). Среднеквадратичная ошибка вычисляется по формуле

,

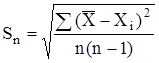где 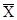- среднее значение искомой величина;

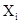- результата отдельных намерений;

n - число опытов.

Более высокой доверительной вероятности должен соответствовать более широкий интервал:

,

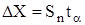. где 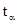- коэффициент Стьюдента, значения которого приведеныв таблице.

Число опытов	Коэффициент 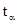при доверительной вероятности
0,90	0,95	0,98	0,99	0,999
	2,92	4,30	6,96	9,92	31,6
	2,35	3,18	4,54	5,84	12,9
	2,13	2,78	3,75	4,60	8,61
	2,02	2,57	3,36	4,03	6,87
	1,94	2,45	3,14	3,71	5,96
	1,89	2,36	3,00	3,50	5,41
	1,86	2,31	2,90	3,36	5,04
	1,83	2,26	2,82	3,25	4,78
	1,81	2,23	2,76	3,17	4,59
	1,80	2,20	2,72	3,11	4,44
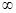	1,60	2,00	2,30	2,60	3,30

В математике доказывается, что если при косвенных измере­ниях искомая величина находится как функция измеряемых на опыте других величин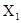 , , 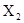,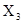…, 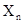то есть

, , ,…, ),

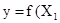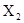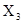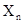то абсолютная погрешность рассчитывается согласно выражению

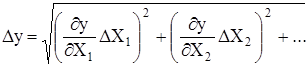
При этом все погрешности аргументов 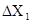, , 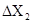,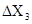…, 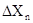должны быть приведены к одной и той же доверительной вероятнос­ти. Та же доверительная вероятность α будет соответствовать .

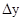Относительная погрешность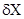определяется как отношение абсолютной погрешности 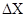к самой измеряемой величине X или

^:

.

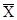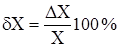Теоретические положения

Моментом инерции материальной точки относительно некоторой оси называют произведение массы данной точки на квадрат рассто­яния ее до данной оси:

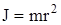
(1.1)

Момент инерции есть величина аддитивная. Это означает, что момент инерции твердого тела относительно данной оси равен сум­ме моментов инерции всех материальных точек тела относительно этой оси:

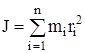. (1.2)

Пределом суммы уравнения (1.2) является интеграл вида

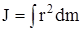, (1.2а)

где t - расстояние от материальной точки массой dm до оси вращения.

Момент инерции является мерой инертности тела при враща­тельном движении, то есть определяет способность вращающихся тел сохранять неизменным свое состояние покоя или равномерного вращения. Момент инерции тела зависит не только от массы тела, но и от ее распределения относительно заданной оси вращения.

Для определения момента инерции используется ряд экспери­ментальных методов, основанных на законах вращательногодвижения.

Описание установки.

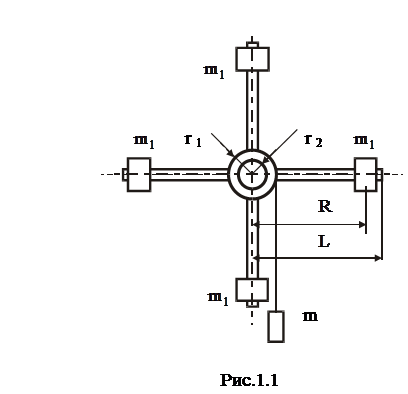.В данной работе требуется определять момент инерции систе­мы, называемой маятником Обербека. Маятник Обербека представляет собой крестовину, со­стоящую из четырех стержней длиной L , жестко закрепленных во втулке с осью (рис. I.I). На стержни крестовин надевают одинаковые грузы массой m₁ , которые могут быть закреплены на разных расстояниях R от оcи вращения. Грузы за­крепляют симметрично, то есть так, чтобы центр тяжести системы находил­ся на оси вращения. Два шкива радиусами r ₁ , r ₂ насажены на ось вращения маятника. На шкив наматываетсянить, к свободному концу которой прикрепляется груз массой m. При падении этого груза нить разматывается и приводит маятник в равноускоренное вращательное движение.

Момент инерции маятника можно найти на основании уравнения динамики вращательногодвижения:

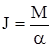(1.3)

где М- результирующиймомент внешних сил, действующих на ма­ятник;

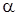- угловое ускорение маятника.

Для определения момента сил М рассмотрим силы, действую­щие на груз m. На груз действует сила тяжести, и сила натя­жения нити 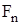, равная и противоположная по направлению силе, действующей на шкив и создающей вращающий момент 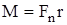. Запишем второй закон Ньютона для груза m:

,

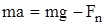откуда

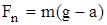(l.4)

Следовательно, вращающий момент сил приложенных к маятнику,

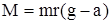(1.5)

Угловое ускорение 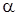определяетсяиз условия

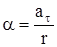, (1.6)

где 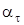- тангенциальное ускорение точек на поверхности шкива, равное ускорению а, с которым движется груз m (нить нерастяжима).

Подставляя уравнения(1.5) и (1.6) в равенство (1.3), получаем

­;

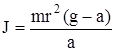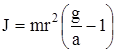. (1.7)

Если ускорение а, с которым движется груз m, намного меньше ускорения свободного падения g, то 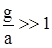, формулу (1.7) можно записать в следующем виде:

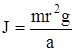. (1.8)

Таким образом, для определения момента инерции системы J надо знать ускорение a, с которым движется груз m . Дляэтогоопределяют время t , за которое груз проходит высоту h.

Как известно,

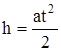
Откуда

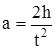. (1.9)

Порядоквыполнения работы.

В качестве груза m в работе используется набор грузов с известными массами. Намотав нить на большой шкив, поднять груз m до соприкосновения с электромагнитом и включить ток в цепи электромагнита. Затем одновременно разомкнуть цепь электромаг­нита и включить электросекундомер. При достижении нижнего кон­такта груз автоматически отключает электросекундомер. Время движения груза t определить по секундомеру. Проделать два аналогичных измерения ( 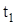, 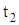) , добавляя грузы. Намотав нить на малый шкив, повторитьизмерения. Полученные данные записать в таблицу.

Шкив	№ п/п	r	m	t	a	J

Обработка результатов эксперимента.

По формуле (1.9) рассчитать ускорение а. Убедившись, что неравенство a<<g выполняется, по формуле (1.8) вычислить момент инерции J.

Произвести расчетабсолютной и относительной погрешности.

Контрольные вопросы.

1. Дать определение угловой скорости, углового ускорения, вращающего момента. Указать единицы измерения этих величин, связь между угловыми и линейными скоростями и ускорениями.

2. Дать определение момента инерции материальной точкии твердого тела относительно данной оси. В чем заключается свойство аддитивности момента инерции системы?

З. Вывести основное уравнение динамики вращательного движения.

4. Как изменится время падения груза m , если грузы маятника m, передвинуть ближе к оси вращения?

5. Вывести расчетную формулу исходя из закона сохранения энергии.

ЛАБОРАТОРНАЯ РАБОТА Я 1.1.2

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАЯТНИКА МАКСВЕЛЛА*

Описание установки.

Маятник Максвелла представляет собой диск, жестко поса­женный на ось. Найти момент инерции маятника можно, решив задачу о скатывании маятника с наклонной плоскости. Наклонная плоскость имеет две направляющие, на которые устанавливается ось маятника, после чего ему предоставляется возможность свободно скатываться.

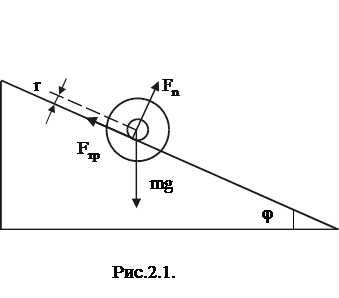
Рассмотрим динамику качения (рис, 2.1), считая, что скольжение полностью отсутствует. На маятник действуют три силы: сила тяжести 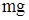, реакция наклонной плоскости 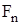и сила трения 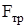.Трение между осью маятника и наклонной плоскостью возникает в точках их соприкосновения. Поскольку эти точки оси в каждый момент времени неподвижны (образуют мгновенную ось вращения),сила трения, о которой идет речь, является силой трения покоя.

Уравнение движения, записанное через проекции сил на направление движения, в нашем случаеимеет вид

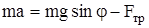(2.1)

Для дальнейших расчетов воспользуемся основным уравнением динамики вращательного движения:

___________________________________

* Теоретические положения приведены в лабораторной работе № 1.1.1.

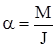(2.2)

где 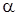- угловое ускорение маятника;

М - суммарный момент внешнихсил;

J- момент инерция маятника

В уравнении(2.2) написанном относительно оси вращения, совпадающей с осью симметрии маятника, будет отличен от нуля толькомомент силы трения

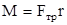(2.3)

При отсутствии скольжения линейное ускорениесистемы а связано с угловым уравнением:

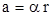(2.4)

Из формул (2.2), (2.3), (2.4) получаем

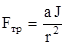(2.5)

Подставляя F_тр в уравнение (2.1), получаем

,

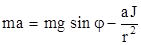откуда

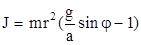. (2.6)

Таким образом, момент инерции маятника Максвелла может быть найден из опыта, если известна масса маятника m, радиус оси r, ускорение свободного падения g и ускорение скатывающегося тела при установке угла наклонной плоскости φ.

Порядок выполнения работы.

Определить массу маятника с помощью рычажных весов и радиус оси штангенциркулем. Измерить высоту наклонной плоскости h и ее длину l. По полученным данным рассчитать .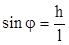

Установить маятник на направляющих наклонной плоскости. Измерить секундомером время скатывания t. Так как движение равноускоренное, то 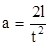. Подставляя значение а в уравнение (2.6), получаем

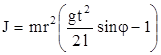. (2.7)

Пренебрегаем вторым слагаемым, стоящим в скобках, окончательно получаем

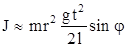. (2.8)

Опыт проводят с двумя маятниками, имеющими одинаковые радиусы осей r, но разные массы. Один из них имеет круговые вырезы. С каждым маятником измерения производят 5 раз, после чего рассчитывают J согласно формуле (2.8). Результаты измерений заносят в таблицу.

Сплошной маятник	Маятник с вырезами
№ п/п	t	J		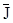№ п/п	t	J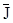

Полученные результаты можно проверить путем теоретического расчета. Пренебрегая моментом инерции оси, для однородного диска относительно оси, проходящей через центр тяжести, имеем:

,

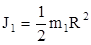где 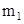-масса диска ( без оси ),

_,

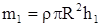где ρ - плотность материала диска (железо);

R - радиус диска ;

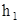- толщина диска.

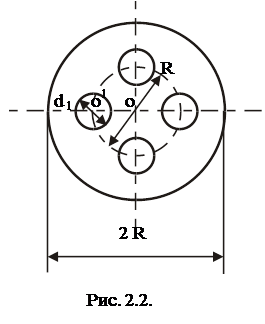Второй маятник имеет 4 круговых выреза, симметрично расположенных относительно его оси (рис.2.2). Центры вырезов находятся на расстоянии 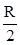от центра диска.

Рассматривая вырезы как отрицательные массы, на основании свойства аддитивности имеем:

,

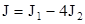где J₂ – момент инерции одного из круговых вырезов

Величину J₂ можно найти по теореме Штейнера:

,

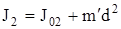где J₀₂ – момент инерции вырезанной части (диска) относительно оси ,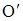

,

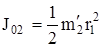где 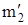- масса выреза, ;

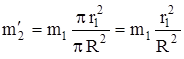r – радиус кривизны;

d – расстояние между осями О и .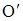

Таким образом, для проведения расчетов надо знать плотность железа, толщину диска h, его радиус R и радиус вырезов r₁.

Штангенциркулем измерить h₁, R, r₁.

Произвести расчет абсолютной и относительной погрешности.

Контрольные вопросы

1. Что называется моментом инерции материальной точки твердого тела ?

2. В чем заключается свойство аддитивности момента инерции ?

3. Сформулировать теорему Штейнера.

ЛАБОРАТОРНАЯ РАБОТА № 1.1.3.

ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ
С ПОМОЩЬЮ ФИЗИЧЕСКОГО МАЯТНИКА.

Теоретические положения.

Физическим маятником называется твердое тело, способное совершать колебания вокруг неподвижной точки (оси), не совпадающей с его центром тяжести. Период малых колебаний физического маятника определяется выражением

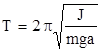, (3.1)

где J - момент инерции маятника относительно заданной оси вращения;

m - масса маятника ;

g - ускорение свободного падения;

а - расстояние от точки подвеса (оси вращения) до центра тяжести маятника.

Если известны T, J, m, a, то уравнение (3.1) позволяет определить ускорение свободного падения

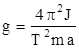, (3.1а)

Описание установки

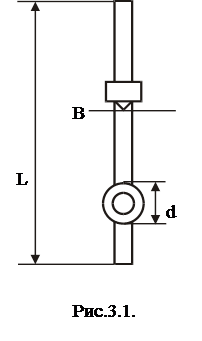
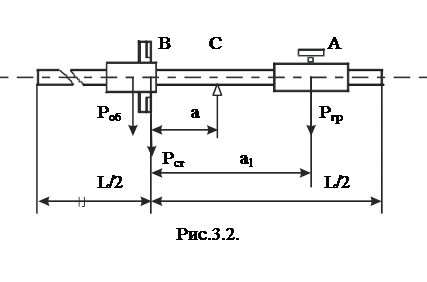
Физический маятник, предлагаемый в данной работе (рис.3.1), представляет собой систему трех тел: стержня массой m _ст и длиной L; груза в виде диска массой m _гр, способного перемещаться вдоль стержня; в средней части стержня находится обойма массой m _об, в которой крепится стержень. В нижней части обоймы расположена призма, ребро которой является осью вращения маятника.

Момент инерции системы на основании свойства аддитивности может быть рассчитан как сумма моментов инерции всех тел, входящих в систему, относительно их общей оси вращения:

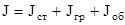_, (3.2)

Момент инерции однородного стержня относительно оси, перпендикулярной стержню и проходящей через центр тяжести, равен

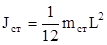, (3.3)

Путем расчета легко убедиться, что в данном опыте груз можно рассматривать как материальную точку, тогда

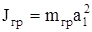, (3.4)

где а ₁ - расстояние от центра тяжести груза до оси вращения маятника.

Моментом инерции обоймы в условиях данного опыта можно пренебречь. Следовательно, момент инерции системы может быть рассчитан из условия

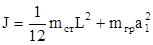, (3.5)

Массы стержня, груза и обоймы, а также длина стержня указаны на стойке прибора. Расстояние а ₁ измеряется с помощью линейки, так как оно может быть выбрано произвольно.

Расстояние от оси вращения до центра тяжести системы может быть найдено путем расчета:

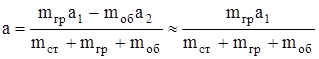, (3.6)

где а ₂ - расстояние от центра тяжести обоймы до оси вращения.

Расстояние а определяется либо по уравнению (3.6), либо опытным путем (по указанию преподователя).

При определении а опытным путем маятник в горизонтальном положении устанавливается на ребро трехгранной призмы так, чтобы он находился в равновесии (3.2). Расстояние от ребра призмы до оси вращения маятника и дает искомую величину а.

Порядок выполнения работы.

Отвернув винт крепления груза, установить его так, чтобы край диска касался конца стержня. С помощью линейки измерить а ₁ и а, как это описано выше. Привести маятник в движение, отклонив его на угол, не превышаюший 5-6^о, и отсчитать по секундомеру время t не менее двадцати (N=20) полных колебаний. Определить период колебания маятника:

.

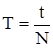Обработка результатов эксперимента.

Считая m _ст, m _гр, m _об известными, рассчитать момент инерции J согласно формуле (3.5). Найти ускорение свободного падения g, используя уравнение (3.1а). (Под m понимается полная масса системы).

Повторить опыт пять раз при различных положениях груза на стержне, последовательно сдвигая его вверх примерно на 5 см.

Данные измерений занести в таблицу.

а	а1	N	t	T	J	g

Произвести расчет абсолютной и относительной погрешности.

Контрольные вопросы.

1. Что называется физическим и математическим маятником ?

2. От чего зависят периоды колебаний физического и математического маятников ?

3. Чем обусловлено и от каких факторов зависит ускорение свободного падения на поверхности земли ?

4. Что понимается под моментом инерции тела относительно данной оси ?

5. Подсчитать процент относительной ошибки, которая допускается в данной работе из-за того, что момент инерции диска принимается равным моменту инерции точечного груза, сосредоточенного в центре диска, используя теорему Штейнера.

ЛАБОРАТОРНАЯ РАБОТА N 1.1.4.

ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ

Теоретические положения

Всякая реальная механическая колебательная система с течением времени теряет свою энергию, которая передается окружающей среде и превращается в другие формы. Если убыль энергии не восполняется извне, то энергия колебания системы начинает постепенно убывать. Как известно, полная энергия колебательного движения материальной точки в данный момент рассчитывается по уравнению

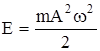, (4.1)

где m - масса;

А - амплитуда;

ω - циклическая частота.

Масса m и частота ω с течением времени не изменяется, следовательно убыль энергии сопровождается уменьшением амплитуды колебания.

Таким образом, реальная колеблющаяся система, предоставленная самой себе, колеблется с постепенным убыванием амплитуды смещения. Такие колебания называются свободными затухающими колебаниями.

Известно, что дифференциальным уравнением движения является второй закон Ньютона. Рассмотрим силы, действующие на нашу систему. В данном случае на колеблющуюся систему действуют квазиупругая сила

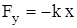, (4.2)

где k - коэффициент упругости;

x - смещение.

и сила сопротивления, которая в случае малых скоростей движения пропорциональна величине скорости:

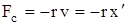, (4.3)

где r - коэффициент сопротивления, зависящий от формы тела и вязкости среды.

Результирующая всех сил, по второму закону Ньютона равна 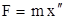. Тогда уравнение движения колеблющегося тела, при условии, что F_у и F_c направлены по одной прямой, будет иметь вид

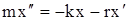, (4.4)

или

.

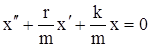Заменив 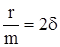и ,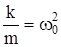

получим

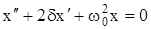, (4.5)

где 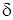- коэффициент затухания, .

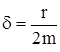Решение уравнения (4.5) имеет вид

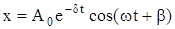, (4.6)

где 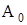- начальная амплитуда смещения;

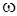- циклическая частота свободных (затухающих) колебаний;

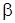- начальная фаза колебаний.

Циклическая частота свободных колебаний может быть рассчитана из соотношения

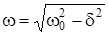, (4.7)

где 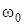- циклическая частота собственных колебаний.

Заменив 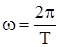, 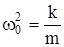и 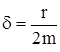, получим период затухающих колебаний

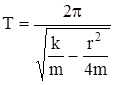. (4.8)

Из уравнения (4.8) видно, что период колебаний системы увеличивается с ростом коэффициента сопротивления среды r. При 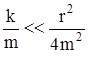система не будет совершать колебаний.

Для оценки степени затухания колеблющейся системы вводят величину, равную отношению двух амплитуд смещения, отличающихся по времени на один период, которая называется декрементом затухания .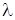

Из уравнения (4.6) следует, что амплитуда смещения убывает с течением времени по закону

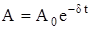, (4.9)

Отсюда декремент затухания равен

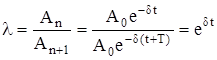. (4.10)

После логарифмирования уравнения (4.10) получим выражение для логарифмического декремента затухания

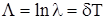, (4.11)

Амплитуда колебаний, отстоящих на один период, мало отличается друг от друга, поэтому для более точного определения логарифмического декремента затухания обычно измеряют амплитуды, отстоящие друг от друга по времени на N периодов.

Из равенства отношений

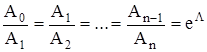
видно, что произведение

.

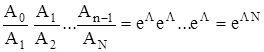Следовательно,

.

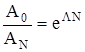Логарифмирование последнего уравнения дает следующее выражение:

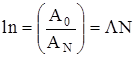или .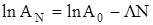

Для вывода рабочей формулы решаем систему уравнений:

;

.

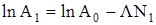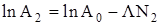Совместное решение этой системы дает следующее выражение :

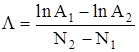. (4.12)

Описание установки

В данной работе предлагается опытным путем определить коэффициент затухания, логарифмический декремент затухания маятника, представляющий собой металлический стержень с диском, который может поворачиваться вокруг вертикальной оси. Маятник снабжен указателем, перемещающимся вдоль шкалы (рис.4.1).

Порядок выполнения работы.

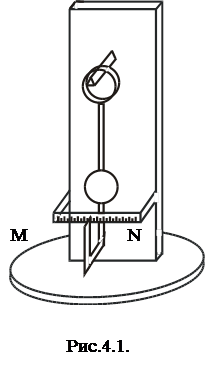Установить диск маятника параллельно плоскости качания. Определить три раза время двадцати полных колебаний. По среднему значению времени вычислить период колебания маятника

.

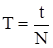Отклонив маятник на 5-6 см. от положения равновесия, отпустить его и определить амплитуду 20, 40, 60 и т.д. колебаний. Получить 8-12 значений амплитуд.

Произвести аналогичные измерения, установив диск маятника перпендикулярно плоскости его качания.

Результаты занести в таблицу.

N	t	A	ln A

Обработка результатов эксперимента.

Построить графики зависимости ln A = f (N) для первого и второго случаев на одном чертеже. Выбрав две наиболее удаленные точки на одной прямой, рассчитать значение Λ по формуле (4.12). Используя уравнение (4.11), вычислить δ. Сделать аналогичные расчеты для второго случая.

Контрольные вопросы.

1. Вывести дифференциальное уравнение затухающих колебаний, записать его решение.

2. Что называют коэффициентом затухания, декрементом затухания, логарифмическим декрементом затухания?

3. Дать определение математического и физического маятников.

4. От чего зависят периоды колебаний физического и математического маятников?

ЛАБОРАТОРНАЯ РАБОТА № 1.1.5.

ИЗУЧЕНИЕ ЯВЛЕНИЯ РЕЗОНАНСА ПРИ ВЫНУЖДЕННЫХ КОЛЕБАНИЯХ

Теоретические положения

Вынужденными называются такие колебания, которые возникают в колебательной системе под действием внешней периодически изменяющейся силы (вынуждающей силы). Пусть вынуждающая сила изменяется со временем по гармоническому закону

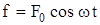, (5.1)

где ω - циклическая частота колебаний вынуждающей силы;

F₀- амплитудное значение вынуждающей силы.

В этом случае установившиеся вынужденные колебания системы также будут гармоническими и период их будет равен периоду колебаний внешней силы. Известно, что дифференциальным уравнением движения является второй закон Ньютона. Для того чтобы написать уравнения движения, рассмотрим силы, действующие на систему. Кроме вынуждающей силы, в системе при свободных колебаниях действуют квазиупругая сила

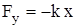, (5.2)

где x - смещение;

k - коэффициент упругости;

и сила сопротивления, которая в случае малых скоростей движения пропорциональна величине скорости :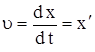

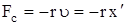, (5.3)

где r - коэффициент сопротивления.

Результирующая всех сил, действующих на колеблющееся тело, по второму закону Ньютона равна

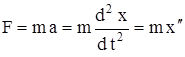. (5.4)

Если силы действуют вдоль одной прямой, уравнение движения запишем следующим образом:

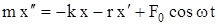. (5.5)

Разделив это уравнение на m и перенеся члены с x и 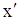в левую часть, получим неоднородное линейное дифференциальное уравнение второго порядка:

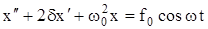, (5.6)

где δ - коэффициент затухания, ;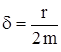

ω₀ - собственная частота колебаний системы, ; .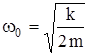

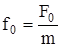Смещение x от положения равновесия будет изменяться со временем по закону

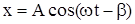, (5.7)

где β - сдвиг фаз между колебаниями системы и колебаниями внешней силы.

Если подставить выражение (5.7) в уравнение (5.1), то можно определить амплитуду вынужденных колебаний:

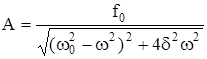, (5.8)

.

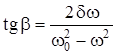Итак, для колебательной системы, имеющей данную собственную частоту и данный коэффициент затухания δ, амплитуда вынужденных колебаний зависит от частоты вынуждающей силы ω. Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы ω к частоте собственных колебаний системы ω₀ получило название резонанса. Частоту вынуждающей силы, при которой возникает резонанс, называют резонансной частотой.

Условие, при котором амплитуда вынужденных колебаний будет максимальна, опредлелим, приравняв к нулю производную 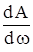, считая 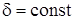. Тогда для резонансной частоты получим:

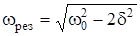. (5.9)

Из этой формулы следует, что в системах, для которых затухание мало ( 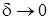), резонанс наступает при частоте вынуждающей силы, близкой к собственной частоте системы ( 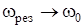). Подставив значение резонансной частоты в формулу (5.8), определим значение резонансной амплитуды:

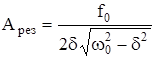, (5.10)

Из уравнения (5.10) следует, что при отсутствии сопротивления среды амплитуда должна обращаться в бесконечность.

Описание установки.

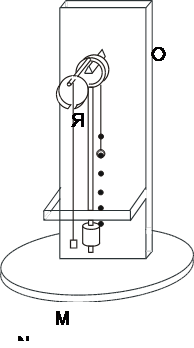
Изучение явления резонанса производится на установке с двумя маятниками (рис. 5.1). Тяжелый маятник, с большим запасом энергии и постоянным периодом колебания T₀, используется в качестве задающего вибратора. Маятник-вибратор представляет собой стержень с тяжелым грузом, укрепленным у его нижнего конца. Ось вращения находится на ребре призмы. В верхней части маятника-вибратора укреплен якорь Я, с помощью которого колебания передаются нити маятника-резонатора.

Маятник-резонатор представляет собой небольшой груз Г, подвешенный на нить. Нить проходит через канал в оси маятника-вибратора, другой конец ее укрепляется на болтах, вмонтированных в стойку прибора на определенных расстояниях друг от друга. Это позволяет легко изменять длину маятника-резонатора.

Горизонтальная шкала МN предназначена для определения амплитуды колебания маятника-резонатора.

Порядок выполнения работы.

Установить минимальную длину маятника-резонатора. Затем, отклонив маятник-вибратор до упора, отпустить его. Толчки маятника-вибратора раскачивают маятник-резонатор. Когда амплитуда его колебаний перестает возрастать, производят отсчет ее значения по горизонтальной шкале.

Во избежание ошибок за счет параллакса глаз в момент отсчета располагают по нормали к шкале. Измерения повторяют при различной длине маятника-резонатора. Амплитуда колебаний маятника-резонатора будет, очевидно, наибольшей при резонансе, когда отношение 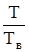мало отличается от 1. Измерения повторяют с другим коэффициентом затухания. При расчетах учитывают, что 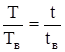, где t, 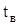- время одинакового числа колебаний маятника-резонатора и маятника-вибратора.

Обработка результатов эксперимента.

Целью работы является построение амплитудной резонансной кривой. Эта кривая графически изображает зависимость амплитуды колебаний маятника-резонатора от отношения его периода колебаний Т к периоду колебаний маятника-вибратора .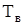

t
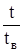A

Контрольные вопросы.

1. Вывести и решить дифференциальное уравнение вынужденных колебаний.

2. Чем вызван сдвиг фаз между колебаниями системы и колебаниями внешней силы? Чему равен этот сдвиг фаз при резонансе и какова его роль в этом явлении?

3. Вывести уравнение для резонансной амплитуды смещения.

4. Вывести уравнение для резонансной частоты.

5. Как изменяется вид амплитудной резонансной кривой при изменении коэффициента затухания?

ЛАБОРАТОРНАЯ РАБОТА № 1.1.6.

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ЖИДКОСТИ

МЕТОДОМ СТОКСА

Теоретические положения

Во всех реальных жидкостях и газах при перемещении одних слоев относительно других возникает более или менее значительные силы трения. Эти силы, носящие название сил внутреннего трения, направлены по касательным к поверхностям слоев. Величина силы внутреннего трения в жидкостях и в газах определяется законом Ньютона:

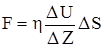, (6.1)

где 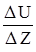- градиент скорости, показывающий изменение скорости на единицу длины в направлении, перпендикулярном скорости;

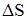- площадь соприкосновения слоев.

Величину 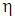, зависящую от природы жидкости и тех условий, при которых она находится, называют коэффициентом внутреннего трения или коэффициентом вязкости. Коэффициент вязкости 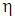численно равен силе внутреннего трения, приходящейся на единицу площади соприкосновения слоев при градиенте скорости, равном единице. Природа внутреннего трения в газах объясняется переносом импульса молекулами из слоя в слой благодаря их тепловому хаотическому движению. В жидкостях механизм внутреннего трения совершенно иной. Молекулы жидкости не обладают полной свободой перемещения и проводят большую часть времени в колебательном движении около положения равновесия. Движущиеся слои увлекают соседние слои в основном за счет сил взаимодействия (сцепления) между молекулами жидкости.

Коэффициент вязкости может быть найден опытным путем. Для этого рассмотрим задачу о падении шарика в вязкой жидкости. На движущийся шарик (рис.1) действуют три силы:

1. Сила тяжести

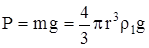, (6.2)

где r – радиус шарика;

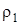- плотность материала шарика;

2. Выталкивающая (архимедова ) сила

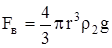, (6.3)

где 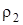- плотность жидкости.

3. Сила сопротивления, которая при малых скоростях движения определяется законом Стокса:

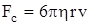. (6.4)

По истечении некоторого времени от начала падения движение становится равномерным, что соответствует условию

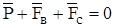, (6.5)

или

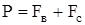. (6.5а)

Используя уравнения (6.2), (6.3) и (6.4), получаем

,

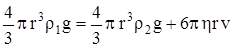откуда коэффициент вязкости

.

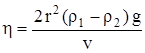Полученное выражение позволяет определить коэффициент вязкости, если известны .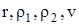

Описание установки.

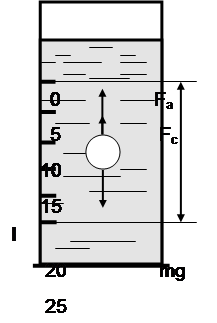Установка для определения коэффициента вязкости методом Стокса (рис. 6.1) представляет собой цилиндрический сосуд с исследуемой жидкостью (смесь глицерина с водой). Сосуд закрыт крышкой, в средней части которой находится отверстие для опускания шариков. На стойке, к которой крепится цилиндр, имеется шкала для отсчетов расстояний, пройденных шариком при падении.

Порядок выполнения работы.

С помощью микроскопа определяют диаметр шарика. Затем опускают его в отверстие крышки и, после того как он пройдет путь 5-10 см, то есть движение его будет установившимся, включают секундомер и измеряют время падения между выбранными метками шкалы. Зная пройденное расстояние l и время движения t, определяют скорость движения 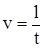. Опыт повторяют не менее пяти раз. Результаты эксперимента заносят в таблицу.

r	l	t	v	η

Производят расчет абсолютной и относительной погрешности.

Контрольные вопросы.

1. Сформулировать закон Ньютона. Дать определение коэффициента вязкости и его единиц измерения.

2. Пояснить механизм внутреннего трения в жидкостях с точки зрения молекулярно-кинетической теории.

3. Сформулировать закон Стокса.

4. Можно ли за начало отсчета l выбирать верхнюю границу жидкости?

5. Выяснить условия равномерного падения шарика в вязкой жидкости.

Литература

Зисман Г.А., Тодес О.М. Курс общей физики. Т.I.- М.: Наука, 1963,-340 с.

Савельев И.В. Курс общей физики. Т. I. - М.: Наука, 1973,- 512 с.

_____________

Оглавление

Краткая теория погрешностей . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3

Лабораторная работа № 1.1.1.

Определение момента инерции маятника Обербека . . . . . . . . . . . . . .5

Лабораторная работа № 1.1.2.

Определение момента инерции маятника Максвелла . . . . . . . . . . . . .9

Лабораторная работа № 1.1.3.

Определение ускорения свободного падения с помощью физического маятника . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12

Лабораторная работа № 1.1.4.

Изучение затухающих колебаний . . . . . . . . . . . . . . . . . . . . . . . . . . . . .15

Лабораторная работа № 1.1.5.

Изучение явления резонанса при вынужденных колебаниях . . . . . . 19

Лабораторная работа № 1.1.6.

Определение коэффициента вязкости жидкости методом Стокса . ..23

Литература . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26

______________

Сергей Петрович АРТЮХОВ,

Виктор Васильевич НЕКРАСОВ,

Злата Георгиевна ИВАЩЕНКО,
Фаина Александровна БОДНАРЮК,
Лидия Федоровна ТРЕНИНА

МЕХАНИКА
Методические указания к выполнению лабораторных работ

Редактор Р.В.БЕЛЯКОВ

Техн.редактор Л.П.КОСТРОВА

Корректор Л.Н.ГЕРОЕВА

_____________________________________________________________

Сдано в произв. 27.03.80. Подписано к печати 25.03.80

Формат 60x84/16. Бумага типографская № 2. Усл. печ.л. 1,86.

Уч.-изд.л. 2.0. Тираж 280 экз. Заказ № 213. Бесплатно.

Редакционно-издательский отдел АЛТИ

_____________________________________________________________

Отпечатано на ротапринте АЛТИ.

Архангельск, 7, набережная им. В.И.Ленина, 17