Вектори. Лінійні операції над векторами
1. Скалярні і векторні величини. Величина, для характеристики якої досить її числового значення у відповідних одиницях вимірювання, називається скалярною. Прикладами скалярних величин є маса, температура, довжина, площа, об’єм, кількість тепла і т.п.
Величина, для характеристики якої крім числового значення вказується ще і напрямок в просторі, називається векторною. Наприклад: сила, швидкість, прискорення, напруженість поля (електростатичного, магнітного, електромагнітного) і т.п.
Геометричним зображенням векторної величини в заданому масштабі є вектор.
Вектором називається відрізок заданої довжини і вказаним напрямком в просторі, тобто направлений відрізок.
 В
В
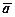
А
Рис. 1
На рис. 1 А - початкова точка вектора, В - кінець вектора, вектор позначають 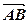 . Для зручності запису замість символа «
. Для зручності запису замість символа « 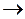 » над вектором будемо писати « — ». Іноді вектор позначають однією буквою:
» над вектором будемо писати « — ». Іноді вектор позначають однією буквою: 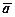 . Відстань від точки А до точки В називають довжиноюабо модулем вектора і позначають
. Відстань від точки А до точки В називають довжиноюабо модулем вектора і позначають 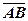 або
або 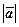 .
.
Якщо початок і кінець вектора збігаються, то такий вектор називається нульовим і позначають 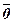 . Напрямок нульового вектора може бути довільним.
. Напрямок нульового вектора може бути довільним.
Два ненульові вектори, що лежать на паралельних прямих або на одній прямій називають колінеарними, позначається 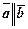 . Нульовий вектор вважається колінеарним довільному вектору.
. Нульовий вектор вважається колінеарним довільному вектору.
Вектори паралельні одній і тій же площині, або ті що лежать в одній площині називаються компланарними.
Рівними називаються два вектори, якщо вони задовольняють умови:
1) вони колінеарні,
2) їх модулі рівні,
3) вони направлені в одну сторону, тобто
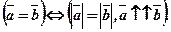
Наприклад, на рис. 2, де АВСD - паралелограм,
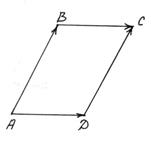
Рис. 2
вектори 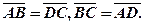
Якщо 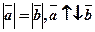 , то вектори
, то вектори 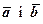 - протилежні. Вектор протилежний вектору
- протилежні. Вектор протилежний вектору 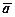 позначають
позначають 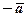 . Вектор
. Вектор 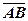 протилежний вектору
протилежний вектору 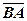 і записують
і записують 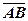 =
= 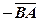 .
.
З означення рівності векторів випливає, що вектор можна переносити в просторі паралельно самому собі, такі вектори називають вільними.
Вектор, модуль якого дорівнює одиниці називається одиничним вектором, або ортом, і позначається 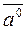 :
:
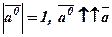 .
.
2. Лінійні операції над векторами. До них відносяться додавання векторів та множення вектора на число (скаляр).
Додавання векторів. Нехай задані два вектори 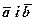 . Відкладемо з деякої точки О вектор
. Відкладемо з деякої точки О вектор 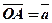 , а тоді з точки А відкладемо вектор
, а тоді з точки А відкладемо вектор 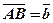 і розглянемо вектор
і розглянемо вектор 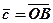 .
.
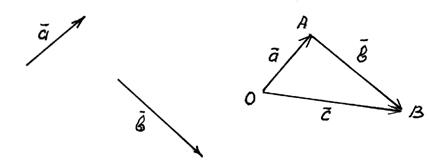
Рис. 3
Сумою двох векторів 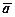 і
і 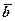 називається вектор
називається вектор 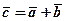 , початок якого знаходиться в початку вектора
, початок якого знаходиться в початку вектора 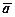 , а кінець - в кінці вектора
, а кінець - в кінці вектора 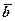 за умови, що початок початок
за умови, що початок початок 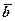 знаходиться в кінці
знаходиться в кінці 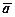 .
.
Згідно рис. 3 вектор 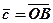 замикає ламану OAB, напрямок вектора
замикає ламану OAB, напрямок вектора 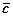 береться в кінець останнього доданка
береться в кінець останнього доданка  .
.
За принципом замикання знаходиться сума більшого числа доданків.
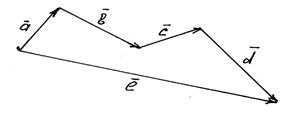
Рис. 4
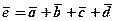 .
.
Різниця векторів. Помістимо початки векторів 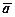 і
і 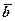 в одну точку О, і побудуємо замикаючий вектор
в одну точку О, і побудуємо замикаючий вектор 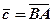 (рис. 5).
(рис. 5).
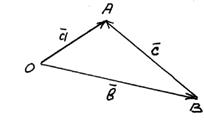
Рис.5
Різницею двох векторів 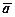 і
і 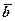 , що виходять з однієї точки, називається замикаючий вектор
, що виходять з однієї точки, називається замикаючий вектор 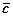 (позначається
(позначається 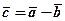 ), напрямок якого вибирається в сторону заменшуваного.
), напрямок якого вибирається в сторону заменшуваного.
Множення вектора на число. Добутком ненульового вектора 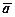 на число
на число 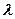 називається вектор
називається вектор 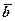 , (позначається
, (позначається 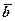 =
= 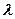
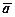 ), колінеарний вектору
), колінеарний вектору 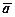 ,модуль якого
,модуль якого 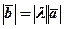 .
.
Напрямок вектора 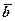 збігається з напрямком вектора
збігається з напрямком вектора 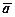 , якщо
, якщо 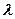 >0, і протилежний напрямку вектора
>0, і протилежний напрямку вектора 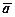 , якщо
, якщо 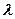 <0, тобто
<0, тобто
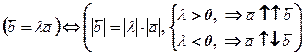
При 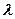 = 0, або
= 0, або 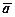 =
= 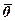 ввжається, що
ввжається, що 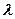
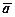 - нульовий вектор.
- нульовий вектор.
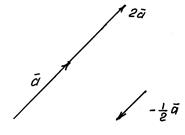
Рис. 6
3. Властивості лінійних операцій над векторами.
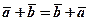
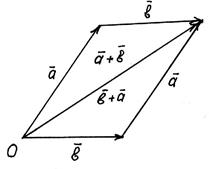 Рис. 7
Рис. 7
Властивість 1, що називається переставною або комутативною, зрозуміла з рис. 7, дозволяє додавати вектори за правилом паралелограма.
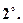
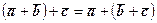 - асоціативна або сполучна властивість (див. рис. 8).
- асоціативна або сполучна властивість (див. рис. 8).
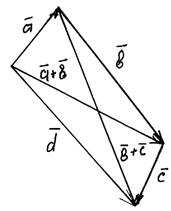
Рис. 8
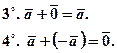
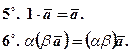
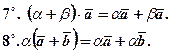
Властивості 3 - 8 пропонуємо перевірити самостійно.
Приклад 1. За даними векторами 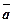 і
і 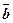 побудувати вектори:
побудувати вектори:
а) 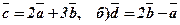 .
.
Розв’язання. Див. на рис. а) і б)
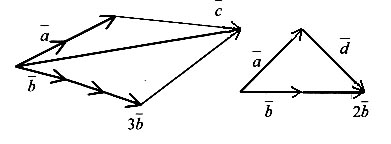
Приклад 2. У трикутнику АВС проведена медіана АМ див. на рис. Виразити вектор 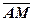 через вектори
через вектори 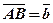 і
і 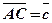 .
.
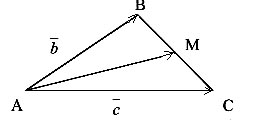
Розв’язання.За означенням різниці векторів 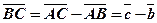 , тоді
, тоді 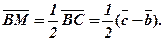
За означенням суми векторів із ∆ АВМ маємо