Практический пример. Расчет площади детали
Конструируется некоторый механизм, для которого нужна деталь данной площади, имеющая форму кругового сегмента. Решением должна быть не формула (выражение, зависящее от r и s), а явно указываемое число, которое должно отличаться от истинного значения корня на некоторую малую величину.
Площадь кругового сегмента с радиусом r и с заданным в радианах центральным углом А равна s=r2(А-sinА)/2.
Рассмотрим задачу определения величины центрального угла по данному радиусу r и площади s. Получим уравнение
x-sin x – 2s/r2=0 (1.6)
По смыслу задачи 0<x<2p и 0<s<pr2.. Уравнение (1.6) - это трансцендентное уравнение.
Точную аналитическую формулу для решения этого уравнения найти трудно. Но можно воспользоваться численными методами для решения такого рода уравнений, учитывая, что надо получить некоторое значение.
Решить самостоятельно эту задачу.
Контрольные вопросы
1.6.1.Перечислить методы численного решения уравнений.
1.6.2 С чего начинается обычно численное решение уравнения?
1.6.3 В чем суть метода простой итерации?
1.6.4 Какое условие должно выполняться для сходимости метода простой итерации?
1.6.5 В чем преимущество и недостаток метода простой итерации?
1.6.6 В чем суть метода половинного деления?
1.6.7 Какие условия должны выполняться при использовании метода половинного деления?
1.6.8 В чем суть метода Поиск решения?
Варианты заданий
Дано действительное положительное число е. Методом деления отрезка пополам, методом итерации и с помощью Поиска решения найти приближенное решение уравнения f(x)=0. Абсолютная погрешность найденного значения не должна превосходить е. Рядом с уравнением дополнительно указан отрезок (в квадратных скобках), содержащий корень, или начальное приближение к корню (в круглых скобках). Если не указано, то для получения отрезков, содержащих по одному корню уравнения, или для получения начальных приближений к корням исследовать график функции. Задания выполнить, используя MS Excel, также написать программу на одном из языков программирования (C++ или Pascal).
1. x+ln(x+0.5)-0.5=0, [0, 2];
2. x5 – x - 0.2=0, [1, 1.1];
3. x4 + 2x3 – x-1=0, [0, 1];
4. x3 –0.2x2 –0.2x-1.2=0, [1, 1.5];
5. x*2x – 1=0, [0, 1];
6. x2 – sin5x = 0, [0.5, 0.6];
7. 5x – 8* ln x = 8; (4.32);
8. 3 x2 – cos 2x – 1 = 0;
9. 2 ln x – 1/x +0.5=0;
10. x2 cos 2x + 1=0, [0, pi/2];
11. 2 x – cos x = 0, [0, pi/2];
12. 0.9 x – sin √ x – 0.1=0, [0, 1.5];
13. tg x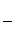 
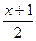= 0, [0, pi/4];
14. (4+x2) (ex –e - x)-18, [1.2, 1.3];
15. 
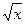+ 1 = cos(0.5x) ;
16. x*2x-1=0, [0,1];
17. x2-1.3*ln(x+0.5)-2.8*x+1.15=0, [2.1, 2.5];
18. x4+cos x -2=0, [0, 2];
19. tg x – x =0, (4.67);
20. 1.8*x4 – sin 10*x = 0, (0.22);
21. x – sin x = 0.25, (1.17);
22. 3*x – sin x-7=0;
23. x – cos x -1 =0;
24. x2 – sin5x = 0, [0.5, 0.6];
25. 2 x – cos x = 0, [0, pi/2];
Задание 2. Методы численного интегрирования
Цель работы:изучение методов численного интегрирования, применение этих методов для инженерных расчетов при решении практических задач.
Многие интегралы даже от элементарных функций не выражаются через элементарные функции. Кроме того, функция, которую надо проинтегрировать, может быть задана не формулой, а как-либо иначе. Интегралы могут выражаться через хорошо изученные и затабулированные неэлементарные «специальные» функции, например, функция ошибок, интегральный синус и интегральный косинус. Наиболее универсальными методами, пригодными к интегралам от произвольных функций, заданных любым способом, в особенности таблично, являются методы численного интегрирования. Формулы численного интегрирования дают приближенные значения определенного интеграла, если известны значения подынтегральной функции в некоторых точках (узлах) интервала интегрирования.
Рассматриваются следующие методы численного интегрирования
1. Приближенное вычисление площади с помощью разбиения на прямоугольники.
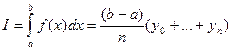
где n – количество отрезков разбиения; y0 бy1,… yn -- значения функции на концах отрезков.
2. Приближенное вычисление площади с помощью разбиения на трапеции.
I=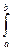 
f(x)dx= 
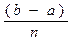(y0+2y1+…+2yn-1+yn),
где n- количество отрезков разбиения; y0 , y1, yn – значения функции на концах отрезков.
3. Метод Симпсона
I=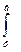 
f(x)dx= 
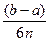(y0+4y1+2y2+…+4y 2n-1+y 2n),
где 2n – количество разбиения; у0, у1, у2n – значения функции на концах отрезков.
Метод Симпсона можно использовать при условии, что количество точек нечетное, и по оси абсцисс точки расположены на одинаковых расстояниях, то есть, интервал постоянный. Шаг интегрирования состоит из двух соседних интервалов между данными.
При применении формулы трапеции, ошибка имеет порядок h2, формулы Симпсона – h4, где h – интервал – расстояние между двумя точками интегрирования. При уменьшении h точность увеличивается.
Методы будут проиллюстрированы на примере данных, описывающих функцию у=соs(х) на интервале от 0 до pi/2.
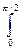соs(х)dx=sin(pi/2) -sin(0)=1 (2.1)
Процесс вычисления можно разделить на этапы:
1. ввод данных;
2. ввод формулы для вычисления площади одного прямоугольника или трапеции;
3. копирование формулы во все интервалы (обратить внимание, что их количество может не совпадать с количеством точек данных);
4. вычисление суммы площадей отдельных фигур разбиения.