Бөлінгіштік және оның қасиеттері

Мазмұны

КІРІСПЕ........................................................................................................... 4

САННЫҢ БҮТІН ЖӘНЕ БӨЛШЕК БӨЛІГІ ҰҒЫМЫ

1.1 Антье функциясы.......................................................................................7

1.2 Антье функцияның қасиеттері..................................................................8

1.3 Антье функцияның кейбір қолданылулары.............................................11

САННЫҢ БҮТІН БӨЛІГІНЕ ҚАТЫСТЫ ЕСЕПТЕРДІ ШЕШУ ЖОЛДАРЫ

2.1 Санның бүтін және бөлшек бөлігі бар теңдеулер...................................18

2.2 Санның бүтін және бөлшек бөлігі бар функциялардың графиктері.....22

2.3 Санның бүтін және бөлшек бөлігі бар теңдеулер жүйесі.......................26

2.4 Санның бүтін және бөлшек бөлігі бар теңсіздіктер................................27

2.5 Математикалық жарыстар есептері.......................................................... 28

2.6 Орта мектептегі математика сабағындағы есеп шығару маңыздылығы

.............................................................................................................................. 30

Қортынды.......................................................................................................... 32

Қосымша............................................................................................................ 35

Пайдаланған әдебиеттер................................................................................. 39

КІРІСПЕ

Білім - өркениеттің өлшемі әрі тетігі болып табылатындықтан, кез-келген мемлекеттің рухани және әлеуметтік дәрежесі білім деңгейіне байланысты бағаланады. Жан-жақты үйлесімді, өркениетті елдің білімді ұрпағын тәрбиелеп шығу бүгінгі мектептің алдына қойған мақсаттарының бірі. Бұл мақсат әрбір орта мектеп мұғалімінен бүгінгі заман талабына сай білім беруді және оқыту әдістемесін жетілдіруді талап етеді.

Математика мектепте оқылатын пәндердің ішіндегі негізгісі, әрі іргелі ғылымдардың бірі. Мектеп бағдарламасындағы математиканың басым бөлігі практикада қолданылады және басқа пәндерді оқытуда негіз бола алады.

Қазіргі таңдағы еліміздегі білім беру жүйесінің ең басты міндеттерінің бірі білім берудің ұлттық моделіне өту арқылы жас ұрпақтың білім деңгейін халықаралық дәрежеге көтеру. Елдің алға қарай дамуының басты шарты – білімділік пен интелект, адамдардың рухани саулығы, дамудың жан–жақтылығы, оның кәсіби дайындығының кеңдігі мен икемділігі.

Мектептегі математикалық білім беруді қайта құрудың негізгі міндеті оқытудың әдістемелік жүйесін дамыту және ақпараттық міндетті атқару функциясының басым болуына байланысты, осы ақпаратты қолдану біліктілігін қалыптасытруға басты назар аудару болып табылады. Жоғары технологиялық өндіріс жағдайында оқушылардың ғылыми, дайындығына, олардың танымдылық қабілеттеріне, сонымен бірге жалпы оқу біліктілігі мен дағдысына қойылатын талап артады.

Әр мемлекеттің адамгершілік интеллектуальдық, экономикалық және мәдени әлуеті білім беру ортасының жағдайы мен оны алға қарай дамытудың мүмкіндіктеріне тәуелді. Осы орайда кез келген мемлекет білім беруді жетілдіруге ерекше көңіл бөліп, бұл салаға басым мемлекеттік маңыз беруді басты мақсат етуі керек. Мемлекет жариялаған оқытудың құндылығы нақты қаржылай, материалдық – техникалық, ақпараттық, құқықтық және ғылыми - әдістемелік жабдықтаумен нығайтылуы тиіс.

Қазіргі педагогиканың түйінді мәселелрінің бірі – балалардың логикалық ойлау қабілетін дамыту, алған білімін тиімді қолдануға үйрету, табиғатқа жақындату мен адамгершілік тәрбие беру. Осы орайда, мектеп пәндерінің ішінде, математиканың алар орыны ерекше.

Бүгінгі таңда, мектепті бітірген соң математик, физик немесе инженер боламын деп мақсат қойған оқушылармен қатар, барлық мектеп бітіруші түлектер үшін жақсы математикалық білім қажет. Белгілі деңгейдегі математикалық дайындығы жоқ адамның, күнен күнге артып келе жатқан қолданыстағы техниканы игеруі де мүмкін емес. Адам қызметінің түрлі облыстарын математикаландыру, компьютердің пайда болуымен және оның қолданысының кеңеуіне байланысты артты. Осының бәрі нақты математикалық білімді, белгілі бір ойлау стилін қажет етеді.

Математиканың өскелең ұрпақты тәрбиелеуде әсерінің көптеген қырлары бар. Математика, оқушы бойындағы ұқыптылық, ынталылық, жаңаны қабылдау тәрізді өзгеріске жиі ұшырайтын әлеуметтік, техникалық, табиғи кұбылыстарға бейімденушілік сияқты жеке қасиеттерінің де дамуына әсер етеді.

Есепті шешу – бұл есепте берілген айқын және жанама сандармен, шамалармен, олардың арасындағы қатыстармен логикалық дұрыс тізбектелген амалдар мен операциялар арқылы есептің талабын орындау.

Математака курсында санның бүтін бөлігі және бөлшек бөлігі тақырыбының алатын орны ерекше. Аталған тақырып мектеп бағдарламасындағы негізгі тақырыпқа жатпағанымен, сабақтан тыс кезеңде жүргізілетін үйірмелер немесе факультативтік сабақтарда санның бүтінжәне бөлшекбөлігіне қатысты есептерді қарастыру оқушылар үшін игілікті шара болары анық. Есептер шығару барында оқушылар математикалық жаңа білімдерді игеріп, практикалық іс-әрекетке дайындалады. Мұндай есептер олардың логикалык ойлау қабілетін дамытуға үлкен әсер етеді. Санның бүтін бөлігі және бөлшек бөлігіне байланысты есептердің ішінде қалыпты емес ойдауды талап ететін есептер жиі кездеседі. Ондай есептерді тек жақсы оқитын оқушыларға ғана емес, барлық оқушыларға ұсыну керек. Әсіресе логикалық ойлау қабілеті төмен оқушыларға мұндай есептер өте қажет.

Математика пәні мұғалімінен жалпы іргелі білім ғана емес, педагогтік қызметке шығармашылықпен қарау, іскерлік белсенділік көрсету арқылы өз білімін үздіксіз жетілдіріп отыру қабілеті де талап етіледі.

Дипломдық жұмыстың мақсаты:

Бөлінгіштіктің қасиеттерін жәненегізгі ұғымдарын және оларды есептерін шешуде қолдану жолдарын талдау. Мектеп оқушыларының бойында есептерді шешу жолдарының жүйесін қалыптастыру – оларды ғылыми білімдер жүйесімен қаруландыру. Оқушылардың ой-өрісін кеңейту, логикалық ойлау қабілетін дамыту.

Дипломдық жұмыстың құрылымы:

Дипломдық жұмыс кіріспеден, екі тараудан және қорытынды мен қосымшадан тұрады.

Кіріспеде жұмыстың өзектілігі,мақсаты айқындалған.

І тарауда сандық функциялар, санның бүтін бөлігі ұғымы, олардың қасиеттері және кейбір қолданулары қарастырылған.

ІІ тарауда санның бүтін және бөлшек бөлігі тақырыбына қатысты есептер, олардың түрлері және шешу жолдары және орта мектептегі математика сабағындағы есеп шығарудың маңыздылығы қарастырылған.

Оқушылардың санның бүтін бөлігі туралы есептерді шешу тәсілін анықтау кезінде (олардың кез келген түрін) оның құрылымын талдауды меңгеруге қажетті шеберлік және шеберлікті қалыптастыру үшін (тікелей сабақ кезінде) қандай талаптар сақталуы керектігі қорытындыда баяндалған.

Әр тақырып бойынша өздігімен шығаруға арналған есептер және бақылау жұмысының үлгілері ұсынылған.

Пайдаланылған әдебиеттер тізімі көрсетілген.

Тақырыптың өзектілігі:

Ықтималдықтар теориясы адам өмірінің әлеуметтік- мәдени, білім беру, ғылыми-өндірістік саласындағы кез-келген мәселені шешуде қолданылатын статистика ғылымының математикалық негізі болып табылады. Бұл мектеп курсында ықтималдықтар теориясы және математикалық статистика негізінің оқытылуының өзектілігін айқындайды. Ал ықтималдықтар теориясы есептерін шешу үшін комбинаторика элементтері қолданылады.

Оқушылардың математиканы меңгеру деңгейі көбінесе олардың математикалық есептерді шығаруға қаншалықты төселгендігі арқылы бағаланады. Сондықтан, комбинаторикалық есептерді шешудің математиканы оқып үйренуде алатын орны ерекше.

Дипломдық жұмыстың мақсаты:

Комбинаториканың негізгі ұғымдарын және оларды ықтималдықтар теориясы есептерін шешуде қолдану жолдарын талдау. Мектеп оқушыларының бойында комбинаторикалық есептерді шешу жолдарының жүйесін қалыптастыру – оларды ғылыми білімдер жүйесімен қаруландыру. Оқушылардың ой-өрісін кеңейту, логикалық ойлау қабілетін дамыту.

Дипломдық жұмыстың құрылымы:

Дипломдық жұмыс кіріспеден, екі тараудан және қорытынды мен қосымшадан тұрады.

Кіріспеде жұмыстың өзектілігі,мақсаты айқындалған.

І тарауда орта мектептегі математика пәнінде қарастырылатын негізгі комбинаторикалық есептердің түрлері, берулі тәсілдері және оларды шешудің жолдары қарастырылған. Оқушыларды комбинаторикалық есептерді талдау жасауға үйретудің және оларды шешу жолдарын меңгерту тәсілдері баяндалған.

ІІ тарауда ықтималдық теориясының элементтері және ықтималдықтар теориясы есептерін шешуде комбинаторика элементтерін қолдану жолдары баяндалған.

Кездейсоқ оқиғалар, оқиғаларға қолдaнылатын амалдар, кездейсоқ оқиғаның ықтималдығы туралы теоремалар талданып, ықтималдыққа қатысты есептерді шешудің әдіс-тәсілдері талданған.

Оқушылардың комбинаторикалық есептерді шешу тәсілін анықтау кезінде (олардың кез келген түрін) оның құрылымын талдауды меңгеруге қажетті шеберлік және шеберлікті қалыптастыру үшін (тікелей сабақ кезінде) қандай талаптар сақталуы керектігі қорытындыда баяндалған.

Әр тақырып бойынша өздігімен шығаруға арналған есептер, тест және бақылау жұмысының үлгілері ұсынылған.

Пайдаланылған әдебиеттер тізімі көрсетілген.

Бөлінгіштік және оның қасиеттері

Жалпы түсініктер

Сандар теориясының негізгі объектісі ретінде 1,2,3,...., натурал сандары, 0 саны және барлық теріс -1,-2,-3,..., сандары алынады. Бұл сандардың барлығы бүтін сандардың жиынын құрайды. Бүтін сандар жиынын 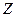деп белгілейді. Яғни,

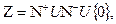
Мұндағы, 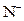- бүтін оң сандар, 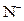- бүтін теріс сандар.

Бүтін сандар жиынының екі не одан да көп элементтеріне қосу, азайту және көбейту амалдарын қолданғанда шығатын элемент те сол жиынның элементі болады. Осы үш амалға қатысты алғанда тұйық болатын, яғни амал қолданғандағы шыққан элемент те сол жиынында жататын, сандар жиынын сақина деп атау қабылданған. Бұдан былайғы жерде өзіміз қарастыратын сақинаны бүтін сандар сақинасы деп атайтын боламыз. Бүтін сандарды қосу, азайту көбейту амалдары, бүтін санның модулі және оның қасиеттері белгілі деп есептеп, бүтін сандар сақинасының элементтерінің бөлінгіштік қасиеттерін қарастырамыз.

1-анықтама. Бүтін және сандары үшін 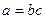болатын бүтін с саны табылса, онда а саны -ға бөлінеді деп атайды.

Егер саны -ға бөлінсе, она 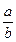арқылы белгілейді.

Бүтін сандар жиыны 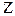-те бұл қатынас төмендегі қасиеттерді қанағаттандырады:

1. Бөлінгіштік қатынасы рефлексивтік, яғни кез келге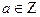н үшін .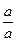

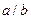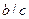2. Бөлінгіштік қатынасы транзитивті, яғни және болса, онда .

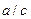3. Егер 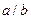болса, онда 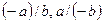және 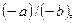яғни бөлінгіштік қатынасы бөлінгіш пен бөлгіштің таңбаларын ауыстырғанда да сақталады.

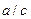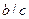4. Егер және болса, онда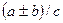

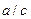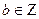5. Егер және , болса онда .

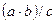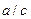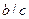6. Егер және болса, онда 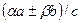, мұндағы, 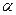және 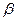кез келген бүтін сандар.

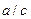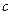7. Егер болып, ал саны -ға бөлінбесе, онда 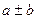саны да с-ға бөлінбейді.

8. Ноль саны кез келген а санына бөлінеді. Себебі,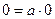

9. Кез келген сан 1 санына бөлінеді. Себебі,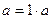

10. Егер а:b болса, онда .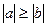

11. Егер 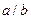және болса, онда 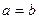не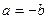

Ескерту. 4 және 5 тұжырымға кері тұжырым дұрыс емес: бірнеше

санның қосындысының бөлінгіштігінен, қосылғыштар бөлінгіштігі, ал көбейтіндінің бөлінгіштігінен көбейткіштердің бөлінгіштігі шықпайды.

Мысалы, 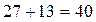саны 8-ге бөлінеді, бірақ 27-де, 13-те 8-ге бөлінбейді. 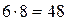саны 12-ге бөлінеді, бірақ не 6, не 8 саны 12-ге бөлінбейді.

Алдықпен бөлу

2-анықтама. Егер q және r бүтін сандары табылып

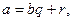
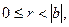(1)

теңдігі орындалса, онда а саны b-ға қалдықпен бөлінеді деп аталады. Мұндағы q-бөлінді, ал r-қалдық деп аталады.

1-теорема. Кез келген бүтін саны бүтін санына қалдықпен бөлінеді және бұл бөлу жалғыз түрде өрнектеледі.

Дәлелдеуі. Әуелі қалдықпен бөлудің бар екенін дәлелдейік. Ол үшін екі жағдайды қарастырамыз.

1) кез келген бүтін сан, ал 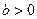болсын.

-ға еселі барлық бүтін сандарды, өсу ретімен орналастырып, қарастырайық: 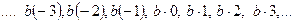санының -дан аспайтын ең үлкен еселігі 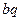болсын. Онда 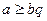демек 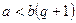яғни 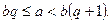Теңсіздіктің барлық жағынан 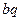-ді шегерсек 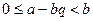теңсіздігін аламыз. 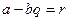деп белгілесек, онда келесі теңдікті аламыз: .

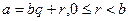2) -бүтін, ал 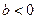болсын.

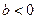болғандықтан 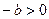, онда 1-ші жағдай бойынша а саны – санына қалдықпен бөлінеді, демек бүтін q және r сандары табылып 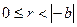немесе 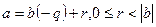орындалады. Кез келген бүтін а және сандары үшін (1) теңдіктің орындалатынын дәлелдедік.

Енді қалдықпен бөлудің, яғни (1) теңдіктің, жалғыз түрде анықталатынын дәлелдейік.

санын -ға бөлгендегі анықталатын (1) өрнек жалғыз емес дейік. Яғни 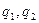және сандары табылып, төмендегі теңдіктер орындалады:

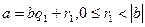және 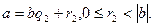Бұл теңдіктерден 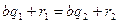немесе 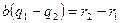шығады.

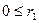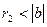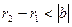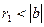және теңсіздіктерінен, , ал және 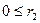теңсіздіктерінен, 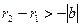теңсіздіктерін аламыз. Яғни, 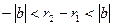, бұдан 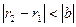. Егер десек, онда 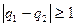және 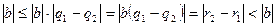. Бұндай теңсіздік мүмкін емес. Ендеше 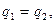ал 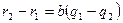болғандықтан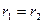

Демек, 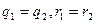болғандықтан (1) түрдегі өрнек жалғыз.