Модели, в которых объясняющие переменные носят как количественный, так и качественный характер

Называются моделями ковариационного анализа (ANCOVA- моделями).

Рассмотрим простейшую ANCOVA - модель с одной ко­личественной и одной качественной переменной, имеющей два аль­тернативных состояния:

y = α + β₁x + β₂d + ε. (4.40)

Пусть, например, y – заработная плата сотрудника фирмы, x – стаж сотрудника, d – пол сотрудника, т. е.

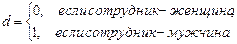
Тогда ожидаемое значение заработной платы сотрудников при х годах трудового стажа будет:

M_у (x, d = 0) = α + β₁x + β₂·0 = α + β₁x – для женщины. (4.41)

M_у (x, d = 1) = α + β₁x + β₂·1 = (α + β₂)+ β₁x – для мужчины. (4.42)

Заработная плата в данном случае является линейной функцией от стажа работы. Причем и для мужчин и для женщин за­работная плата меняется с одним и тем же коэффициентом пропор­циональности β₁. А вот свободные члены в моделях (4.41), (4.42) от­личаются на величину β₂. Проверив с помощью t-статистики статисти­ческие значимости коэффициентов α и (α + β₂), можно определить, имеет ли место в фирме дискриминация по половому признаку. Если эти коэффициенты окажутся статистически значимыми, то, очевидно, дискриминация есть. Более того, при β₂ > 0 – она будет в пользу муж­чин, при β₂ < 0 – в пользу женщин.

В данном случае пол сотрудников имеет два альтернативных значения, и в модели это отражается одной фиктивной переменной. Возникает вопрос, нельзя ли с помощью большего числа фиктивных переменных обрисовать более сложные комбинации? Например, пусть

y = α + β₁x + β₂d₁ + β₃d₂+ ε. (4.43)

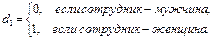
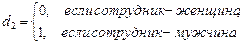
Но в этой ситуации между переменными d₁ и d₂ существует строгая линейная зависимость: d₂ = 1 – d₁. Мы попадаем в ситуацию совершенной мулътиколлинеарности, при которой коэффициенты β₂ и β₃ однозначно определены быть не могут. Простейшим способом преодоления данной проблемы является отбрасывание одной из фиктив­ных переменных и использование для рассматриваемой задачи модели (4.40). Применяя аналогичные выкладки, можно получить следующее общее правило:

Если качественная переменная имеет к альтернативных значе­нии, то при моделировании используются только (к - 1) фиктивных переменных.

Если не следовать данному правилу, то при моделировании ис­следователь попадает в ситуацию совершенной мультиколлинеарности или так называемую ловушку фиктивной переменной.

Значения фиктивной переменной можно изменять на противопо­ложные. Суть модели от этого не изменится. Например, в модели (4.40) можно положить, что:

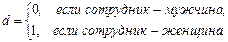
Однако при этом знак коэффициента β₁ изменится на противопо­ложный.

Значение качественной переменной, для которого принимается d = 0, называется базовым или сравнительным. Выбор базового зна­чения обычно диктуется целями исследования, но может быть и про­извольным.

Коэффициент β₁ в модели (4.40) иногда называется дифференци­альным коэффициентом свободного члена, т. к. он показывает, на ка­кую величину отличается свободный член модели при значении фик­тивной переменной, равном единице, от свободного члена модели при базовом значении фиктивной переменной.

Пусть рассматривается модель с двумя объясняющими перемен­ными, одна из которых количественная, а другая – качественная. При­чем качественная переменная имеет три альтернативы, Например, си­туация, связанная с расходами на содержание ребенка, может быть связана с доходами домохозяйств и возрастом ребенка: дошкольный, младший школьный и старший школьный. Так как качественная пере­менная связана с тремя альтернативами, то по общему правилу моделирования необходимо использовать две качественные переменные. Таким образом, модель может быть представлена в виде:

y = α + β₁x + β₂d₁ + β₃d₂+ ε. (4.44)

где y - расходы. x - доходы домохозяйств.

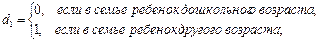
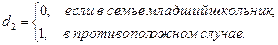
Таким образом, получаются следующие зависимости.

Средний расход на дошкольника:

M_у (x, d₁ = 0, d₂ = 0) = α + β₁x. (4.45)

Средний расход на младшего школьника:

M_у (x, d₁ = 1, d₂ = 0) = α + β₁x + β₂·1 + β₃·0 = (α + β₂)+ β₁x . (4.46)

Средний расход на старшего школьника:

M_у (x, d₁ = 1, d₂ = 1) = α + β₁x + β₂·1 + β₃·1 = (α + β₂+ β₃)+ β₁x . (4.47)

Здесь β₂, β₃ – дифференциальные свободные члены. Базовым зна­чением качественной переменной является значение «дошкольник». После определения коэффициентов регрессии (4.44) определяется статистическая значимость коэффициентов β₂, β₃ на основе t-статистики. Если коэффициенты оказываются статистически незначимыми, то можно сделать вывод, что возраст ребенка не оказывает существенного влияния на его содержание.