Потенциалы Ликнара – Вихерта и поле точечного заряда
Пусть имеется точечный заряд движущийся со скоростью 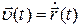 ,
, 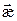 отвечает точке наблюдения,
отвечает точке наблюдения,  интегрируем.
интегрируем.
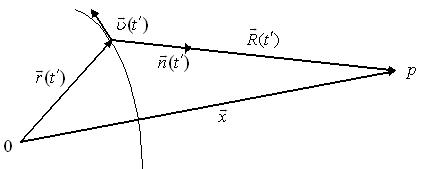
Формулы (20) - (21) для запаздывающих потенциалов можно объединить в одну для 4- потенциала 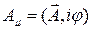 . Тогда можно написать
. Тогда можно написать
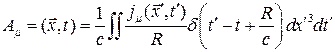 (1)
(1)
где 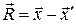 , а
, а 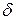 - функция обеспечивает запаздывание потенциалов. Так как рассматривается движение точечного заряда q, то для
- функция обеспечивает запаздывание потенциалов. Так как рассматривается движение точечного заряда q, то для
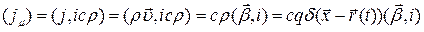
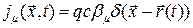 (2)
(2)
где 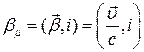 (3)
(3)
Интегрирование по объёму проводится сразу
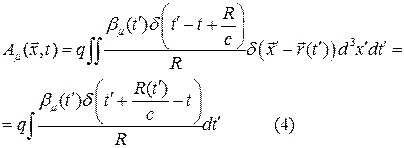
где теперь 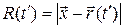 .Для интегрирования по
.Для интегрирования по 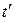 воспользуемся известным соотношением
воспользуемся известным соотношением
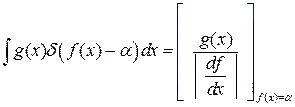 (5)
(5)
В нашем случае т.е.
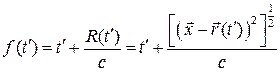
Следовательно
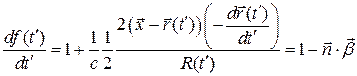
т.е. 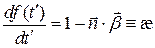 (6),
(6), 
Интегрирование с использованием дает потенциалы произвольным образом движущегося заряда – потенциалы Ликнара – Вихерта:
 (7)
(7)
где индекс запаздывающий означает, что величины в (7) следует брать в момент времени 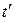 , определяемый из соотношения
, определяемый из соотношения
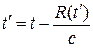 (8)
(8)
Для нерелятивистского движения 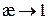 .
.
Используя определение 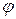 и
и 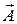 для векторов
для векторов 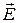 и
и 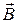 можно найти
можно найти
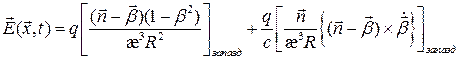
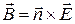 (9)
(9)
Первое слагаемое зависит лишь от 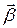 и фактически имеет статический характер, убывая с расстоянием, как
и фактически имеет статический характер, убывая с расстоянием, как 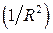 .
.
Вторая линейно зависит от 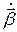 и является типичным поперечным полем излучения, для которого
и является типичным поперечным полем излучения, для которого 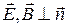 и изменяется как
и изменяется как  .
.
