Структурный анализ механизмов
К ВЫПОЛНЕНИЮ КУРСОВОГО ПРОЕКТА
ПО ДИСЦИПЛИНЕ
„ТЕОРИЯ МЕХАНИЗМОВ И МАШИН”
(для студентов специальностей 7.090214 “Подъемно- транспортные, строительные, дорожные, мелиоративные машины и оборудование” и 7.090258 „Автомобили и автомобильное хозяйство”
очной формы обучения)
Утверждено
на заседании кафедры
«Подъемно- транспортные, строительные, дорожные машины и оборудование»
Протокол № 2 от 22.09.2006 г.
Макеевка 2006
 |
УДК 621.01
Методические указания к выполнению курсового проекта по дисциплине «Теория механизмов и машин» (для студентов специальностей 7.090214 “Подъемно- транспортные, строительные, дорожные, мелиоративные машины и оборудование” и 7.090258 „Автомобили и автомобильное хозяйство” очной формы обучения) / Сост.: В.П. Мельник, Н.А. Юрченко, А.Н. Клен – Макеевка: ДонНАСА, 2006. – 112 с.
В методических указаниях даны теоретические предпосылки и примеры решения задач, составляющих содержание курсового проекта.
Составители: доц. В.П. Мельник
асс. Н.А. Юрченко
асс. А.Н. Клен
Рецензенты: доц. А.В. Гаврюков
доц. Т.В. Луцко
Ответственный за выпуск: проф. В.А. Пенчук
 | |||||
 | |||||
 |
СОДЕРЖАНИЕ
1 Структурный анализ механизмов……………………………………5
1.1 Общие понятия………………………… 5
1.2 Классификация кинематических пар, кинематических цепей механизмов………………………………………… 7
1.3 Число степеней свободы механизма 10
1.4 Принцип Ассура структурного строения и образования
плоских рычажных механизмов 11
2 Кинематический анализ плоских рычажных механизмов 16
2.1 Общие понятия 16
2.2 Траектории и разметка траекторий точек механизмов 16
2.3 Построение плана скоростей и ускорений для плоского
рычажного механизма 18
2.4 Особенности построения плана скоростей и ускорений
для кулисного механизма 25
2.5 Построение кинематических диаграмм для выходного звена 30
3. Силовой анализ механизма 34
3.1 Общие сведения 34
3.2 Пример силового расчета 36
3.2.1 Расчет структурной группы, состоящей из звеньев 4 и 5 37
3.2.2 Расчет структурной группы, состоящей из звеньев 2 и 3 41
3.2.3 Расчет начального звена 45
3.3 Определение уравновешивающей силы методом рычага Жуковского 48
3.4 Особенности кинетостатического анализа для кулисного механизма 51
4 Динамический синтез маховика 54
4.1 Определение момента инерции маховика 54
4.2 Определение геометрических размеров маховика 65
5. Расчет кулачковых механизмов 67
5.1 Общие понятия 67
5.2 Анализ и синтез кулачковых механизмов 69
5.2.1 Центральный кулачковый механизм, в котором кулачок работает по толкателю с острием 69
5.2.2 Дезаксиальный кулачковый механизм, в котором кулачок работает по толкателю с острием 72
5.2.3 Центральный кулачковый механизм, в котором кулачок работает по толкателю с роликом 74
5.2.4 Дезаксиальный кулачковый механизм, в котором кулачок перемещает толкатель с роликом 75
5.2.5 Кулачковый механизм, в котором кулачок перемещает плоский толкатель 76
5.2.6 Кулачковый механизм, в котором кулачок перемещает коромысло с острием 78
5.2.7 Кулачковый механизм, в котором кулачок перемещает коромысло с роликом 80
5.2.8 Кулачковый механизм, в котором кулачок работает по плоскому колебателю 81
6 Проектирование эвольвентного зубчатого зацепления 84
6.1 Геометрические размеры зацепления 84
6.2 Построение картины эвольвентного зацепления для нормальных колес 87
6.3 Качественные показатели зубчатой передачи 92
7 Проектирование сложного зубчатого зацепления 94
7.1 Общие сведения 94
7.2 Механизмы многоступенчатых зубчатых передач с неподвижными осями (параллельными и пересекающимися) 97
7.3 Механизмы многоступенчатых передач с подвижными осями 99
7.4 Синтез планетарных механизмов 103
Список литературы 111
Структурный анализ механизмов
1.1 Общие понятия
Механизм (рис. 1.1) представляет собой систему твердых тел (звеньев), которые образуют друг с другом подвижные соединения, называемые кинематическими парами.
Звенья, входящие в состав механизма, являются упругими телами. Однако их деформации весьма малы, поэтому при исследовании механизмов ими в одних случаях пренебрегают, в других (например, при определении напряжений в звеньях, изучении колебательных процессов и т.п.)- учитывают.
Как правило, одно из звеньев является неподвижным или принимается за неподвижное. Такое звено называется стойкой. Все другие звенья являются подвижными.
Среди звеньев механизма имеются по крайней мере два смежных звена, закон относительного движения которых считается известным. Кинематическую пару, которую образуют два указанных звена, называют входной. Возможны два случая: 1) одно из указанных звеньев является стойкой; 2) оба звена подвижны.
Большинство применяемых в технике механизмов отвечает первому случаю. В таких механизмах подвижное звено, образующее кинематическую пару со стойкой, называется входным звеном. Входному звену сообщается движение относительно стойки, преобразуемое механизмом в требуемое движение других звеньев.
В четырехзвенном механизме (рис. 1.1, а) входную пару образуют стойка 0 и входное звено 1 (здесь и далее на рисунках входное звено отмечено стрелкой, показывающей направление его движения).
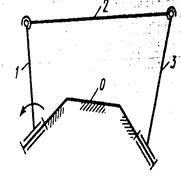
Однако достаточно часто встречаются механизмы, отвечающие второму случаю. Пример такого механизма приведен на рис. 1.1, б. Такие механизмы применяются в грузоподъемных, землеройных и других машинах. В данном случае не представляется возможным конкретно указать входное звено среди двух звеньев, образующих входную кинематическую пару.
Среди подвижных звеньев выделено также выходное звено. Выходным называется звено, совершающее движение, для выполнения которого и предназначен механизм. В механизме может быть несколько входных и несколько выходных звеньев, но чаще всего механизм имеет одно входное и одно выходное звено.
Система звеньев, связанных кинематическими парами, называется кинематической цепью. В состав любого механизма входит кинематическая цепь. Однако не следует отождествлять понятия «кинематическая цепь» и «механизм». Механизм отличается от кинематической цепи, в частности тем, что в механизме указывается стойка и входное звено (точнее - входная кинематическая пара). Механизм можно изобразить техническим чертежом, кинематической схемой или структурной схемой.
Структурная схема- это схема механизма, указывающая стойку, подвижные звенья, входные и выходные звенья, виды кинематических пар (см. дальше). Структурная схема выполняется с помощью определенных условных обозначений, принятых при графическом изображении звеньев и кинематических пар различных видов. Структурная схема механизма используется на этапе структурного анализа и изображается без учета геометрических размеров его звеньев. Между тем, такие геометрические свойства механизма, как взаимная параллельность или перпендикулярность осей отдельных кинематических пар и некоторые другие, обычно учитываются в структурной схеме.
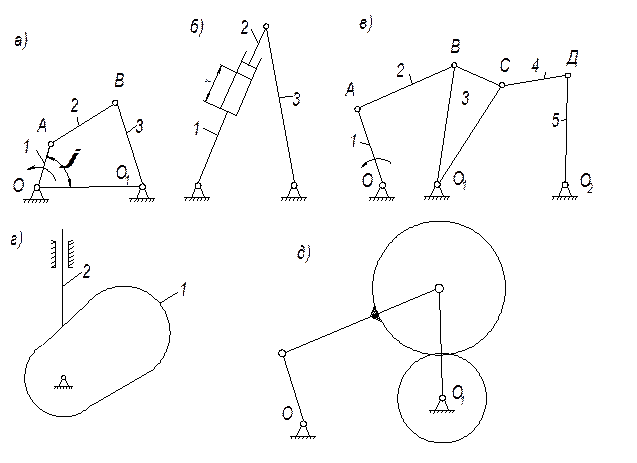
Рис. 1.1
Кинематическая схема, в отличие от структурной схемы, изображается с учетом геометрических размеров звеньев, которые используются при кинематическом анализе. Такие размеры называют параметрами кинематической схемы механизма.
При рассмотрении вопросов структуры и кинематики механизмов обычно принимают следующие допущения: звенья механизма являются абсолютно твердыми телами; отсутствуют погрешности изготовления звеньев; отсутствуют зазоры в подвижных соединениях звеньев.
На рис. 1.1 показаны примеры структурных схем для механизмов, где приняты обозначения: 0- стойка, 1,2,3,4,5- подвижные звенья; 1- входное звено (рис. 1.1 а, в-д); (φ-угловая координата входного звена 1 (рис. 1.1, а); х- линейная координата, устанавливающая относительное перемещение во входной кинематической паре Р12, образуемой звеньями 1 и 2 ( рис. 1.1, б).
1.2 Классификация кинематических пар, кинематических цепей механизмов
Совокупность поверхностей, линий и отдельных точек звена, по которым оно может соприкасаться с другим звеном, образуя кинематическую пару, называется элементом кинематической пары.
Кинематические пары делятся на низшие и высшие. Низшей называется кинематическая пара, в которой относительное движение двух звеньев может быть получено постоянным соприкосновением ее элементов по поверхности. Высшей называется кинематическая пара, в которой относительное движение двух звеньев может быть получено только соприкосновением ее элементов по линиям или в точках.
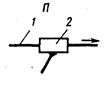
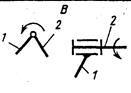
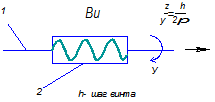
В табл. 1.1 приведены девять видов существующих пар с условными и буквенными обозначениями, числом их степеней свободы. Из таблицы видно, что к низшим относятся поступательная (П), вращательная (В), винтовая (ВИ), цилиндрическая (Ц), сферическая с пальцем (Сп), сферическая (С) и плоскостная (Пл) пары, к высшим – «цилиндр- плоскость», «шарнир- плоскость». Вращательную пару называют шарниром.
На рис. 1.2 показаны стрелками относительные движения звеньев 1 и 2, образующих пару, для пар вида П, В, Ви, Ц, Сп и С. В паре вида Сп цилиндрический палец А, принадлежащий звену 2, может перемещаться в сферической обойме звена 1, причем срединная плоскость прорези проходит через центр сферы. Здесь возможны такие относительные перемещения звеньев 1 и 2: а) поворот вокруг оси пальца; б) поворот вокруг оси, перпендикулярной срединной плоскости прорези и проходящей через центр сферы. В сферической паре возможны повороты относительно трех взаимно перпендикулярных осей, проходящих через центр сферы.
Из определения плоского механизма следует, что его звенья могут образовывать друг с другом одно- или двухподвижные пары. При этом одноподвижные пары являются низшими, а двухподвижные — высшими. В качестве одноподвижных пар в плоском механизме обычно используют вращательную или поступательную пару, а в качестве двухподвижных—любую из двух высших пар, указанных в табл. 1.1, которые в данном случае вырождаются в пару «круг—прямая». В плоском механизме оси всех вращательных пар должны быть взаимно параллельны, а оси поступательных пар — перпендикулярны осям вращательных пар.
 |  |  |
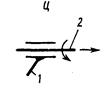 | 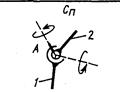 | 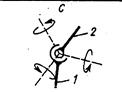 |
Рис. 1.2
Механизмы, звенья которых образуют низшие кинематические пары вида П, В, Ви, Ц, Сп и С (см. табл. 1.1), называют рычажными. Рычажный механизм, звенья которого образуют только вращательные пары, называется шарнирным. В плоском рычажном механизме звенья образуют только одноподвижные пары вида В или П.
В технике наиболее распространены четырехзвенные плоские рычажные механизмы — шарнирный четырехзвенник (см. рис. 1.1, а), кривошипно-ползунный механизм (рис. 1.3) и кулисный механизм (рис. 1.4). Кроме того, к четырехзвенным относятся еще восемь видов механизмов, различающихся числом и порядком расположения вращательных и поступательных пар (однако число поступательных пар не должно превышать двух).
За звеньями рычажного механизма, в зависимости от характера их движения, закрепились определенные наименования. Кривошипом называется звено, которое образует вращательную пару со стойкой и может совершать полный оборот вокруг оси этой пары. Коромыслом называется звено, которое образует вращательную пару со стойкой и может совершать только неполный оборот вокруг оси этой пары. С подвижным звеном кривошип и коромысло образуют, как правило, вращательную или сферическую пару. Ползун — это звено, образующее поступательную пару со стойкой и движущееся прямолинейно- поступательно. Шатуном называется звено, образующее кинематические пары только с подвижными звеньями. Кулиса — это звено, вращающееся вокруг неподвижной оси и образующее с другим подвижным звеном поступательную пару. Так, в механизмах, изображенных на рис. 1.1,а, 1.3 и 1.4, звено 1 является кривошипом или коромыслом, звено 2—шатуном, звено 3—кривошипом или коромыслом (на рис. 1.1, а), ползуном (на рис. 1.3) или кулисой (на рис. 1.4).
Таблица 1.1
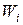 , число степеней свободы , число степеней свободы | 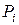 , класс кинем. пары , класс кинем. пары | Вид пары | Условное обозначение | Низшая или высшая | |
| буквенное | графическое | ||||
| Поступательная | П | 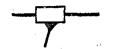 | Низшая | ||
| Вращательная | В | 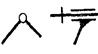 | « | ||
| Винтовая | Ви | 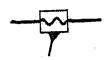 | « | ||
| Цилиндрическая | Ц |  | « | ||
| Сферическая двухподвижная (сферическая с пальцем) | Сп | 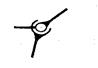 | « | ||
| Сферическая (трехподвижная) | С |  | « | ||
| Плоскостная | Пл | 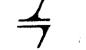 | « | ||
| Цилиндр- плоскость | Ц-Пл |  | Высшая | ||
| Шар- плоскость | Ш-Пл | 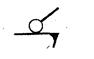 | « |
Существуют три разновидности шарнирного четырехзвенника (см. рис. 1.1, а): 1) кривошипно-коромысловый механизм (входное звено 1—кривошип, звено 3—коромысло), 2) двухкривошипный механизм (звенья 1 и 3 — кривошипы), 3) двухкоромысловый механизм (звенья 1 и 3—коромысла).
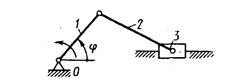 |
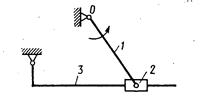
Рис. 1.3 Рис. 1.4
 |
К механизмам с высшими парами относятся кулачковые и зубчатые механизмы. Находят применение также комбинированные механизмы, например, зубчато-рычажный механизм (см. рис. 1.1, д). В машинах применяют и другие виды механизмов - фрикционные, механизмы с гибкими связями (ременная передача, цепная передача), волновые зубчатые передачи (механизмы с гибкими звеньями), дающие возможность передавать движение через герметичную стенку, гидравлические и пневматические механизмы и т. д. Рис. 1.5
1.3 Число степеней свободы механизма
В теоретической механике обобщенными координатами механической системы называют независимые между собой параметры, однозначно определяющие положение системы. Так как механизм — это система связанных между собой твердых тел (звеньев), одно из которых является неподвижным (стойкой), то понятие «обобщенные координаты» может быть распространено и на механизм. Обобщенными координатами механизма называются независимые между собой параметры (линейные или угловые), однозначно определяющие положение всех звеньев механизма относительно стойки.
Число обобщенных координат называется числом степеней свободы или подвижностью механизма. Из определения механизма следует, что его подвижность не может быть меньше 1.
Большинство механизмов, применяемых в технике, имеют одну обобщенную координату и, соответственно, одну степень свободы. Но встречаются и механизмы с двумя степенями свободы и более.
В качестве обобщенных координат механизма обычно принимают относительные перемещения звеньев, образующих входные пары. Например, в шарнирном четырехзвеннике в качестве обобщенной координаты принимается угловая координата φ входного звена 1 (см. рис. 1.1,а). В механизме, показанном на рис. 1.1,б, за обобщенную координату принимается линейный параметр 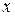 .
.
Если все связи в кинематических парах, приведенные в табл. 1.1, геометрические, т. е. налагают ограничения только на положения (координаты точек звеньев), в этом случае число степеней свободы механизма равно числу обобщенных координат механизма (числу независимых возможных перемещений).
Общее число координат, определяющих положение 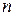 подвижных звеньев механизма, равно
подвижных звеньев механизма, равно 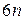 . Каждая одноподвижная кинематическая пара даст пять уравнений связей, в которые входят координаты звеньев, каждая двухподвижная - четыре уравнения и т. д. Если все уравнения связей независимы, то ни одно из них не может быть получено как следствие других.
. Каждая одноподвижная кинематическая пара даст пять уравнений связей, в которые входят координаты звеньев, каждая двухподвижная - четыре уравнения и т. д. Если все уравнения связей независимы, то ни одно из них не может быть получено как следствие других.
Разность между общим числом координат и числом уравнений, связывающих эти координаты, дает число независимых обобщенных координат механизма:
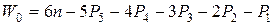 (1.1)
(1.1)
где 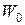 называется основной подвижностью;
называется основной подвижностью;
Р5-число пар 5-го класса;
Р4- число пар 4-го класса и т. д.
Полученное выражение называется универсальной структурной формулой Сомова- Малышева.
Для плоских механизмов (Р3=Р2=Р1=0) структурная формула имеет вид:
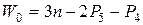 (1.2)
(1.2)
Формула (1.2) называется формулой Чебышева.
Для плоских рычажных механизмов (Р4=Р3=Р2=Р1=0)
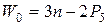 (1.3)
(1.3)
В формулах (1.2) и (1.3) Р5 есть число одноподвижных (низших) пар, а Р4- число двухподвижных (высших) пар.
1.4 Принцип Ассура структурного строения и образования плоских рычажных механизмов
Московский профессор Л.В. Ассур, изучавший строение одноподвижных плоских шарнирных механизмов первого типа, в 1914 г. сформулировал общий принцип их образования (или строения). Впоследствии этот принцип был распространен и на другие рычажные механизмы.
В соответствии с принципом Ассура, механизм может быть разделен на две части: 1) начальный механизм, содержащий стойку и входные звенья; 2) ведомую цепь, содержащую все другие звенья механизма (предполагается, что кинематические пары, посредством которых ведомая цепь присоединяется к начальному механизму, отнесены к ведомой цепи).
Начальный механизм имеет столько же степеней свободы W, сколько и рычажный механизм, из которого он получен. Если ведомую цепь отсоединить от начального механизма и посредством тех же кинематических пар присоединить к стойке, то образуется статически определимая ферма. Это означает, что ведомая цепь обладает нулевой подвижностью относительно тех звеньев начального механизма, к которым она присоединяется. Кинематическая цепь, которая обладает указанным выше свойством ведомой цепи и не может быть расчленена на составляющие кинематические цепи, каждая из которых обладает тем же свойством, называется структурной группой или группой Ассура. Из свойства ведомой цепи следует: либо она есть структурная группа, либо ее можно разделить на две или более структурные группы.
Среди кинематических пар структурной группы имеются внутренние и внешние. Внутренние пары образуют друг с другом звенья данной группы, внешние пары служат для присоединения звеньев данной группы к звеньям начального механизма или других групп.
Для плоского механизма условию структурной группы 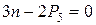 удовлетворяют следующие варианты (табл. 1.2):
удовлетворяют следующие варианты (табл. 1.2):
Таблица 1.2
| Число подвижных звеньев n | ||||
| Число кинематических пар пятого класса Р5 |
Т. е. структурные группы могут быть двухзвенными, четырехзвенными, шестизвенными и т. д.
Основой структурной группы является замкнутый контур. Класс контура определяется числом пар, в которые входят образующие его звенья.
Начальному звену присваивают I класс, звену с двумя парами- II класс, жесткому звену с тремя парами- III класс (треугольник), контуру с четырьмя парами- IV класс (табл. 1.3) и т. д.
Порядок структурной группы определяется количеством поводков, которыми структурная группа присоединяется к начальным звеньям и стойке или к звеньям предшествующих структурных групп.
Наибольшее распространение получили разновидности групп ІІ класса 2-го порядка (табл. 1.3), обычно называемые двухповодковыми группами Ассура, которые отличаются друг от друга сочетанием вращательных и поступательных пар.
Таблица 1.3
| Схема | 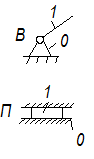 | 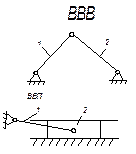 | 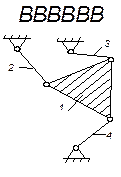 | 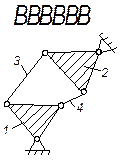 |  |
| Класс контура | I | II | III | IV | V |
| Порядок |
Таким образом, любой рычажный механизм первого типа можно представить в виде начального механизма и одной или нескольких структурных групп. В свою очередь, последовательно присоединяя структурные группы к начальному механизму или к другим структурным группам (метод наслоения), можно получить схему любого рычажного механизма первого типа. В этом и заключается принцип Ассура образования (или строения) механизмов.
Существует определенный порядок следования групп Ассура (если их две и более) в механизме. Первая группа Ассура присоединяется своими внешними парами к звеньям начального механизма, т. е. к стойке и входным звеньям. Каждая последующая группа Ассура присоединяется своими внешними парами к стойке, входным звеньям или к звеньям предшествующих групп. При этом все внешние пары данной группы не могут быть присоединены к одному и тому же звену.
Считается, что класс плоского рычажного механизма совпадает с наивысшим классом входящих в него групп Ассура.
Наиболее широкое применение в технике нашли одноподвижные плоские рычажные механизмы с числом звеньев 4 и 6 (включая стойку). На рис. 1.6, а-з приведены все возможные схемы шестизвенных шарнирных механизмов. Первые пять из них (рис. 1.6, а-д) относятся ко второму классу, три последующих (рис. 1.6, е-з) – к третьему классу.
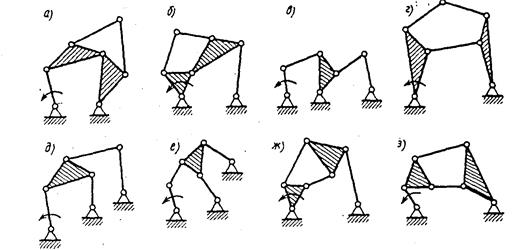
Рис. 1.6
Рассмотрим пример. Пусть необходимо провести структурный анализ механизма, показанного на рис. 1.7.
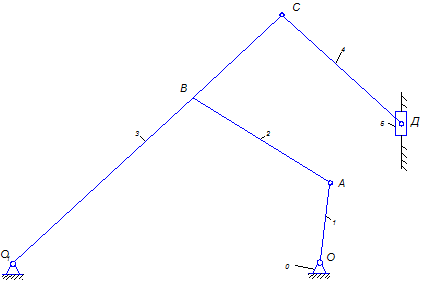
Рис. 1.7 -Структурная схема механизма
Число подвижных звеньев- 5 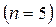 .
.
Звено 1- кривошип, 2 и 4 – шатуны, 3- коромысло, 5- ползун.
Кинематические пары: 0-1- вращательная V класса; 1-2- вращательная V класса; 2-3- вращательная V класса; 3-0- вращательная V класса; 3-4- вращательная V класса; 4-5- вращательная V класса; 5-0- поступательная V класса.
Количество кинематических пар пятого класса - 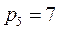 .
.
Степень подвижности механизма
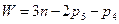
где n-число подвижных звеньев, 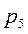 - число кинематических пар 5-го класса,
- число кинематических пар 5-го класса, 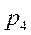 - число кинематических пар 4-го класса.
- число кинематических пар 4-го класса.
В данном случае:
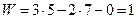
Структурные группы (группы Ассура) показаны на рис. 1.8.
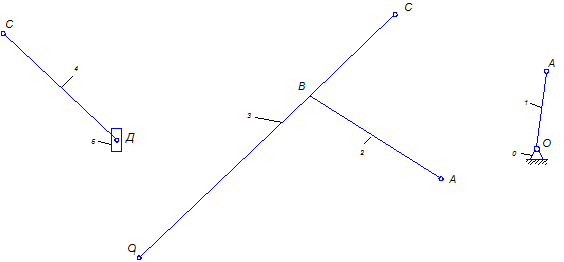
а) б) в)
Рис. 1.8 - Разбиение механизма на структурные группы: а) ІІ класс, 2 порядок (ВВП); б) ІІ класс, 2 порядок (ВВВ); в) ІІ класс, начальное звено
Механизм относится ко второму классу.
