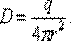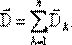Дипольный момент диэлектрика. Диэлектрическая восприимчивость веществ.
16) Дипольный момент диэлектрика (P) - векторная физическая величина, характеризующая, наряду с суммарным зарядом, электрические свойства системы заряженных частиц в смысле создаваемого ею поля и действия на неё внешних полей.
Диэлектрическая восприимчивость вещества - физическая величина, мера способности вещества поляризоваться под действием электрического поля.
Диэлектрическая восприимчивость 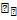 — коэффициент линейной связи между поляризацией
— коэффициент линейной связи между поляризацией
диэлектрика P и внешним электрическим полем E в достаточно малых полях:
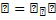
| 17.Вектор электрического смещения |   |
| Имеем границу раздела двух сред с а б Рис. 4.10 Как мы уже показали, в соответствии с (4.1.10),
т.е., напряженность электростатического поля E изменяется скачком при переходе из одной среды в другую. Главная задача электростатики – расчет электрических полей, то есть Для упрощения расчетов была введена новая векторная величина – вектор электрического смещения (электрическая индукция):
Из предыдущих рассуждений
Таким образом, вектор
где Таким образом, вектор В СГС: В СИ: Для точечного заряда в вакууме Для
|
18.С е г н е т о э л е к т р и к и - вещества, обладающие спонтанной поляризацией, направление которой может быть изменено с помощью внешнего электрического поля. Сегнетоэлектрики обладают рядом специфических свойств, которые проявляются лишь в определенном диапазоне температур. Температура Тк (сегнетоэлектрическая точка Кюри) является температурой фазового перехода, ниже этой температуры сегнетоэлектрик обладает доменной структурой и характерными сегнетоэлектрическими свойствами; выше этой температуры происходит распад доменной структуры и сегнетоэлектрик переходит в параэлектрическое состояние. Следствием доменного строения сегнетоэлектриков являются нелинейная зависимость их поляризованности или электрической индукции от напряженности электрического поля (см. рисунок 7.8), которая носит название диэлектрической петли гистерезиса, и резко выраженная температурная зависимость диэлектрической проницаемости, в которой максимум диэлектрической проницаемости достигается при температуре, соответствующей точке Кюри.
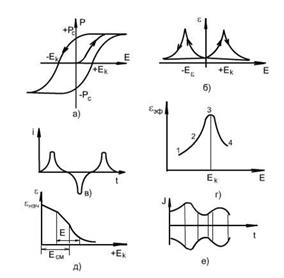
Рис. 7.8. Основные нелинейные свойства сегнетоэлектриков
а – диэлектрический гистерезис; б – динамическая нелинейность; в–нелинейный ток через сегнетоконденсатор; г – эффективная нелинейность; д – реверсивная нелинейность; с – амплитудная модуляция.
На рисунке приведены зависимости основных параметров сегнетоэлектриков (поляризации, диэлектрической проницаемости, тока и напряжения на обкладках сегнетоконденсатора), характеризующих нелинейные свойства в зависимости от напряженности электрического поля (зависимости а),б),г),д)) и времени приложения переменного электрического поля (зависимости в) и е)).
19.Сила тока — физическая величина , равная отношению количества заряда 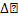 , прошедшего через некоторую поверхность за время , к величине этого промежутка времени
, прошедшего через некоторую поверхность за время , к величине этого промежутка времени 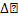
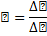
Пло́тность то́ка — векторная физическая величина, имеющая смысл силы электрического тока, протекающего через элемент поверхности единичной площади]. При равномерном распределении плотности тока и сонаправленности её с нормалью к поверхности, через которую протекает ток, для величины вектора плотности тока выполняется:
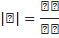

где I — сила тока через поперечное сечение проводника площадью S
Закон Ома для участка цепи:
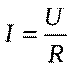
 — сила тока в цепи,
— сила тока в цепи,
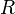 — сопротивление всех внешних элементов цепи,
— сопротивление всех внешних элементов цепи,
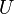 — напряжение
— напряжение
20) Закон Ома в дифференциальной форме.
 σ – удельная проводимость
σ – удельная проводимость
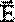 - напряженность электрического поля
- напряженность электрического поля
21) Электродвижущая сила (ЭДС) – Это физическая величина, равная отношению работы, совершенной сторонними силами при перемещении электрического заряда по замкнутой цепи, к этому заряду (ε) [В]
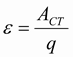
Закон Ома для полной цепи:
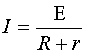
E- ЭДС
R - сопротивление цепи
r- внутреннее сопротивление источника
Правила Кирхгофа.
Правила Кирхгофа – это соотношения между токами и напряжениями, выполняемые на участках произвольной электрической цепи.
Формулировка правил осуществляется через вспомогательные понятия узла, контура и ветви электрической цепи:
1. Ветвь электрической цепи – любой входящий в цепь двухполюсник.
2. Узел электрической цепи (точка разветвления) – точка соединения нескольких ветвей (от 3 и больше)
3. Под контуром электрической цепи понимают замкнутый цикл ветвей, то есть такой путь по цепи, однократное прохождение которого (через ветви и узлы) заканчивается в узле, с которого был начат проход.
Первое правило.
Рассмотрим первое правило Кирхгофа, иначе называемое правилом токов Кирхгофа. Оно вытекает из закона сохранения заряда и звучит следующим образом: алгебраическая сумма всех токов в любом узле произвольной цепи равняется нулю. В виде формулы это выглядит так: I1+I2+..In=0
При расчете, токи, втекающие в узел, считаются со знаком «плюс», а вытекающие из узла – со знаком «минус».
Второе правило
Правило напряжений Кирхгофа, чаще называемое вторым правилом Кирхгофа, является следствием закона сохранения заряда. Оно звучит следующим образом: алгебраическая сумка падений напряжений, на всех ветвях произвольного замкнутого контура, равняется алгебраической сумме ЭДС (электродвижущих сил) ветвей этого контура. Если в данном контуре нет источников ЭДС (идеальных источников напряжения), то сумма падение напряжений в этом контуре равна нулю. В виде формулы это выглядит так: E1+E2+…+En=R1*I1+R2*I2+…+RnIn
При расчете, падение напряжения исходят из следующих правил: если ток в ветви совпадает с выбранным направлением обхода контура, то падение напряжения на этой ветви считают со знаком «плюс». Если ток в ветви направлен против направления обхода контура, то падение напряжения берут со знаком «минус». В частном случае расчета цепи из одного контура, второе правило Кирхгофа вырождается в закон Ома для цепи.
Законы Вольта.
1. При тесном соприкосновении двух разнородных металлов между ними возникает разность потенциалов. Контактная разность потенциала зависит от их химического состава контактирующих веществ и их температуры.
2. Для нескольких контактных веществ контактная разность определяется первым и последним потенциалом
Контактные явления.
Контактные явления – явления, возникающие при прохождении электрического тока через контакт полупроводника с металлом или через контакт двух различных полупроводников с разным типом носителей заряда и их концентрацией.

 и
и 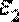 , так что,
, так что, 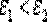 (рис. 4.10, а).
(рис. 4.10, а). 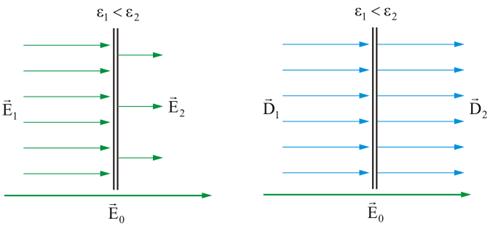
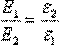 или
или 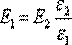 ,
,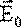 в различных электрических аппаратах, кабелях, конденсаторах, и т.д. Эти расчеты сами по себе не просты, да еще наличие разного сорта диэлектриков и проводников еще более усложняют задачу.
в различных электрических аппаратах, кабелях, конденсаторах, и т.д. Эти расчеты сами по себе не просты, да еще наличие разного сорта диэлектриков и проводников еще более усложняют задачу.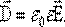
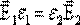 , тогда
, тогда 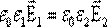 , отсюда
, отсюда
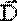 остается неизменным при переходе из одной среды в другую (рис. 4.10, б), и это облегчает расчет
остается неизменным при переходе из одной среды в другую (рис. 4.10, б), и это облегчает расчет 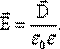
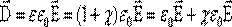 , отсюда можно записать:
, отсюда можно записать: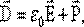
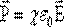 – вектор поляризации, χ – диэлектрическая восприимчивость среды, характеризующая поляризацию единичного объема среды.
– вектор поляризации, χ – диэлектрическая восприимчивость среды, характеризующая поляризацию единичного объема среды.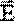 – главной характеристики поля и
– главной характеристики поля и 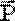 – поляризации среды.
– поляризации среды. поэтому в вакууме
поэтому в вакууме 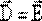 и размерность у
и размерность у 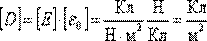 , т. е. это заряд, протекающий через единицу поверхности.
, т. е. это заряд, протекающий через единицу поверхности.