Тема 6 кривые линии и поверхности

Вопросы самоконтроля

1. Дайте определение плоской и пространственной кривых линий. Приведите примеры.

2. Какие точки кривой называются особыми?

3. Как узнать по чертежу что кривая плоская?

4. Какие кривые линии называются гелисами и как их задают на чертеже Монжа?

5. Что называется определителем поверхности?

6. Как образуются поверхности с плоскостью параллелизма?

7. Как образуется линейчатый гиперболоид?

8. Как образуются винтовые поверхности?

9. Что называется каркасом поверхности?

Упражнения

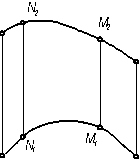
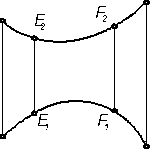
8.1.1 Определить какая кривая задана на чертеже, плоская или пространственная. Построить касательную к кривой в точке

1)M 2)N 3) E 4) F

8.1.2Построить проекции окружности m с центром в точке O и радиусом R=20 мм, лежащей в плоскости Σ.

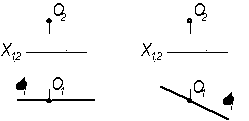
8.1.3 По заданной проекции видимой точки, принадлежащей поверхности найти другую проекцию этой точки.

1)	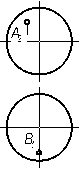2)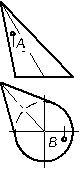
3)	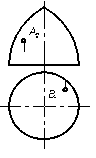4)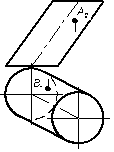

Задачи.

8.2.1 Построить проекции круга диаметром 40 мм, принадлежащего плоскости α (l║n) если дана фронтальная проекция центра круга.	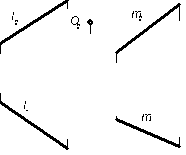8.2.2 Построить горизонтальную проекцию отрезка ABCD цилиндрической поверхности, заданной определителем Р( l и m) и горизонтальную проекцию точки M , лежащей на этой поверхности.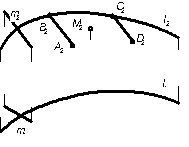
8.2.3 Построить очерк косой плоскости ABCD, заданной определителем: прямыми m и n и плоскостью параллелизма П1. Определить горизонтальную проекцию точки Е, принадлежащей плоскости.	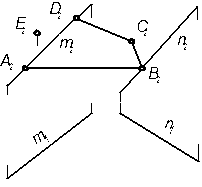8.2.6 Постройте горизонтальную проекцию криволинейного четырехугольника ABCD, лежащего на поверхности конуса вращения, и определите типы кривых второго порядка, дугами которых образован этот четырехугольник.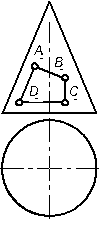

8.2.4 Построить проекции одного витка цилиндрической винтовой линии, проходящей через точку А, заданную на поверхности цилиндра и имеющую шаг равным 60 мм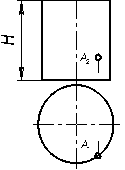

8.2.5 Построить фронтальную проекцию линии n лежащей на конической поверхности Q(S,ν)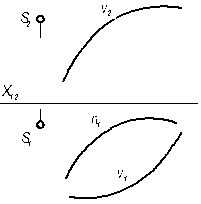

Примеры решения задач:

Задача 1 Определение вида кривой : плоская или пространственная.

Решение Если кривая плоская, то одноименные проекции произвольных секущих (АС) и (BD) пересекутся в точках, лежащих на одной линии связи.

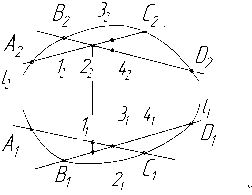
В примере точки 1, 2 и 3, 4 являются конкурирующими, следовательно кривая пространственная.

Дополнительные задачи

8.4.1 Построить проекции прямого кругового конуса, основание которого лежит на плоскости Р(fxh), а вершина в точке S. Точка А принадлежит окружности основания конуса.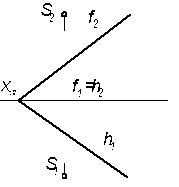

8.4.2 Построить проекции участка цилиндрической винтовой линии радиуса R в пределах одного шага, проходящей через точки А и В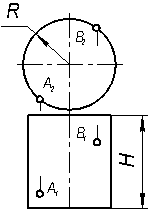

8.4.4 Построить проекции прямого кругового конуса, если точка S – вершина конуса, а точка О – центр окружности основания. Окружность основания одной своей точкой касается пл. П ₂ .

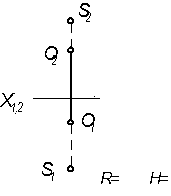
8.4.3 Построить горизонтальную проекцию кривой АВСDE, принадлежащей плоскости треугольника TMN, по заданной фронтальной проекции этой кривой.