Свойства симметрии пространства и времени

Рассмотрим замкнутую систему.

Замкнутая система материальных точек – это система точек, взаимодействующих между собой и не взаимодействующих с точками, не принадлежащими, данной системе.

1.Для замкнутой системы реализуется принцип однородности времени.

Это означает, что мы по временной оси начало отсчёта можем выбрать произвольно. Допустим, мы вели наблюдения в течение времени 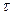,этот отрезок времени можно на оси t взять в любом месте, процесс не изменится. Вследствие однородности времени для замкнутых систем функция Лагранжа явно не зависит от времени, т.е.

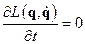
Найдём производную функции Лагранжа по времени:

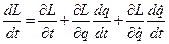
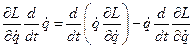
Подставим второе уравнение в первое:

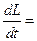
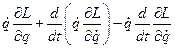
В силу уравнения движения Лагранжа:

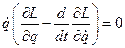
Тогда:

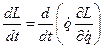
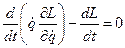
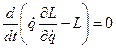
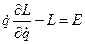- интеграл движения, но только для стационарных связей.

В случае многих степеней свободы:

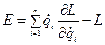
В случае стационарных связей кинетическая энергия есть квадратичная форма скоростей.

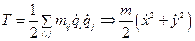
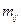- коэффициенты, имеющие не обязательно смысл массы.

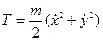
В силу теоремы Эйлера об однородных функциях:

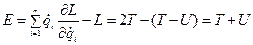
Однородность пространства.

Пространство называется однородным, если уравнения движения (эволюции) системы не зависят от трансляции (переноса как целого) системы в пространстве.

Уравнения движения замкнутой системы инвариантны относительно пространственных трансляций системы как целого. В этом случае реализуется закон сохранения импульса:

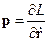или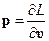

, ,

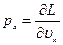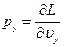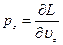
Для замкнутой системы:

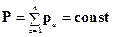
Иногда системы, будучи не замкнутыми, допускают трансляции вдоль некоторых осей. Например, система в однородном поле силы тяжести, допускает трансляции, в плоскости ортогональной вектору напряжённости этого поля -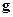

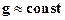- у поверхности Земли.

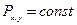
Изотропность пространства.

Уравнения движения замкнутой системы не изменяются при вращении системы как целого относительно любой оси. Другими словами, уравнения движения инвариантны относительно вращения вокруг любой оси. В этом случае реализуется закон сохранения момента импульса:

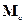- момент импульса материальной точки a.

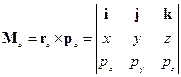
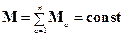
Для незамкнутой системы существуют поля, допускающие вращение системы как целого относительно некоторых осей.

Пример:

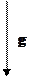Если выбрать z вдоль 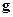, то систему можно вращать как целое вокруг z, в данном поле будет сохраняться проекция момента импульса на направление поля.

Рассмотрим теперь центральное поле. Например, гравитационное поле Земли (сферически симметричное).

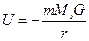
Центр Земли – это центр поля тяготения. Вращение вокруг любой оси, проходящей через центр симметрии, не меняет уравнения движения.

С и l системы.

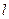-система, это лабораторная система.

Для 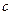-системы:

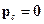
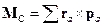
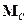- момент импульса относительного движения, т.е. в 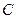-системе.

Энергия:

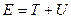
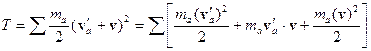
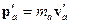
Тогда:

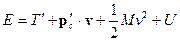
Второе слагаемое здесь обращается в нуль, и мы получаем:

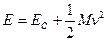, где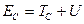

Циклические координаты.

Считаем что пространство однородно и изотропно.

Пусть 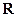-центр масс. Инвариантность 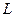относительно трансляции системы как целого означает, что 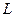не зависит от этих переменных, т.е.

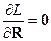
Переменные, от которых функция Лагранжа явно не зависит, называются циклическими.

Если задать ориентацию системы как целого набором углов Эйлера и осуществить вращение системы как целого, то 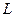не должна зависеть от этих углов:

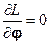
В общем случае, если переменная 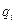является циклической, то

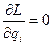
Но тогда в силу уравнения движения Лагранжа:

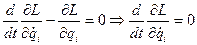
а значит

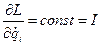
Таким образом, с помощью циклической координаты можно понизить число степеней свободы решаемой задачи.