АЛГЕБРА и начала математического анализа
ФЕДЕРАЛЬНАЯ СЛУЖБА ИСПОЛНЕНИЯ НАКАЗАНИЙ
Федеральное КАЗЕННОЕ образовательное учреждение ВЫСШЕГО образования
Пермский ИНСТИТУТ
(ФКОУ ВО ПЕРМСКИЙ ИНСТИТУТ ФСИН РОССИИ)
ПРОГРАММА
вступительного испытания по общеобразовательному предмету
«Математика»
Пермь
Пояснительная записка
Данная программа адресована абитуриентам, поступающим в Пермский институт ФСИН России, и предназначена для оказания методической помощи при подготовке к вступительному испытанию по математике.
В содержание программы входит список тем, на основе которого составляются задания для вступительного испытания. В конце программы помещены контрольные вопросы и список литературы, рекомендуемой для подготовки к вступительному испытанию по математике.
При составлении программы вступительного испытания по математике авторы руководствовались Образовательным стандартом среднего общего образования по математике, Примерной программой среднего общего образования по математике, кодификатором требований к уровню подготовки выпускников общеобразовательных учреждений для проведения единого государственного экзамена по математике в 2014 году (подготовлен Федеральным государственным бюджетным научным учреждением «Федеральный институт педагогических измерений»).
В общеметодическом отношении абитуриентам при выполнении любого вида задания рекомендуется пользоваться следующей принципиальной схемой.
1. Внимательно прочитать условие (текст задачи, уравнение, неравенство и т.п.) и проанализировать его.
2. Определить исходные данные (то, что дано) и то, что требуется найти.
3. Выбрать необходимую стратегию решения (теоремы, правила, формулы, последовательность операций и т.п.) и записать их в общем виде.
4. Если нужно, сделать поясняющую решение схему, рисунок, чертеж.
5. Провести решение в общем виде, т.е. выполнить математические выкладки.
6. Выполнить численные расчеты, если это требуется по условию задания.
7. Если необходимо, произвести проверку.
8. Четко, грамотно и понятно записать окончательный ответ.
В идеальном варианте (если имеется достаточно для этого времени) математические выкладки и вычислительные операции нужно выполнять два раза (на черновике) для самопроверки правильности решения и расчетов.
В отношении технической стороны вопроса подготовки к экзамену абитуриенту нужно знать следующее:
на экзамене категорически запрещается пользоваться книгами, учебниками, какими-либо учебными пособиями печатного и рукописного характера, шпаргалками, мобильными телефонами);
не разрешается пользоваться при вычислениях микрокалькуляторами;
все записи вначале оформляются на черновике, а затем переносятся на чистовик ручкой с пастой синего или черного цвета; рисунки, схемы выполняются с помощью карандаша и линейки.
Основные требования и умения в области математики, которыми должен обладать абитуриент для успешной сдачи теста.
На экзамене по математике абитуриент должен показать:
четкое знание математических определений и теорем, умение применять теоремы на практике;
умение точно и сжато выражать математическую мысль в письменном изложении, использовать соответствующую символику;
уверенное владение математическими знаниями и навыками, умение применять их при решении задач.
Основные математические понятия и факты, которыми должен владеть поступающий (уметь правильно их использовать при решении задач, ссылаться при обосновании решения):
АЛГЕБРА и начала математического анализа
1. Натуральные числа (N). Простые и составные числа. Делитель, кратное. Наибольший общий делитель. Наименьшее общее кратное.
2. Признаки делимости на 2, 3, 5, 9 и 10.
3. Целые числа (Z). Рациональные числа (Q), их сложение, вычитание, умножение и деление. Сравнение рациональных чисел.
4. Действительные числа (R), их представление в виде десятичных дробей.
5. Изображение чисел на числовой прямой. Модуль действительного числа, его геометрический смысл.
6. Числовые выражения. Выражения с переменными, формулы сокращенного умножения.
7. Степень с натуральным и рациональным показателем. Арифметический корень.
8. Логарифмы, их свойства.
9. Одночлен и многочлен.
10. Многочлен с одной переменной. Корень многочлена на примере квадратного трехчлена.
11. Понятие функции. Способы задания функции. Область определения и множество значений функции.
12. Производная функции. Ее физический и геометрический смысл. Свойства производной. Таблица производных.
13. График функции. Возрастание и убывание функции; периодичность, четность, нечетность.
14. Достаточное условие возрастания (убывания) функции на промежутке. Понятие экстремума функции. Необходимое условие экстремума функции. Достаточное условие экстремума. Наибольшее и наименьшее значение функции на заданном множестве.
15. Определение и основные свойства функций: линейной y = ax + b; квадратичной y = ax2 + bx + c; степенной y = axn, обратной пропорциональности y = k/x; показательной y = ax, логарифмической y = logax; тригонометрических (y = sinx, y = cosx, y = tgx, y = ctgx); арифметического квадратного корня y = 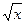 .
.
16. Уравнение. Корни уравнения. Понятие о равносильных уравнениях.
17. Неравенства. Решения неравенства. Понятие о равносильных неравенствах.
18. Система уравнений и неравенств. Решения системы.
