Свободные электромагнитные колебания

ЗАДАЧИ

1. Устройство для дефибрилляции создаёт в районе сердца шок, разряжая конденсатор, заряженный до напряжения 5000 В. Сопротивление тела между электродами равно 500 Ом. Какова будет сила тока в начале разрядки конденсатора? Через 6 мс напряжение на конденсаторе упадет до 250 В. Какова ёмкость устройства?

2. Используя условие предыдущей задачи, определите сколько энергии высвобождается при этом разряде.

3. В интегрирующей цепи ёмкость конденсатора С=0,1 мкФ, а сопротивление R=5000 Ом. Рассчитайте постоянную интегрирования.

4. Прямоугольный импульс частотой 10000 Гц имеет длительность 10-5с. Определите скважность и коэффициент заполнения.

5. Определите постоянную дифференцирования, если ёмкость конденсатора С=0,5мкФ, а сопротивление R= 1000 Ом.

Лабораторная работа №12

Определение параметров импульсных сигналов, используемых для электростимуляции.

Цель работы:Используя осциллограф С8-19, источник питания постоянного тока Б5-45, дифференцирующие и интегрирующие цепи. получить практические навыки определения параметров импульсного сигнала.

Оборудование: осциллограф С8-19, источник питания постоянного тока Б5-45, дифференцирующие и интегрирующие цепи.

Ход работы:

Подготовка установки к работе.

Включите в сеть осциллограф иисточник питания постоянного тока. Установите на источнике питания выходное напряжение 9,5В и ток 50mA. Чувствительность осциллографа установите 2 В/дел, а время развертки – 10mc. Напряжение от источника питания используется для работы мультивибратора. Внешний вид установки приведен на рис.1.

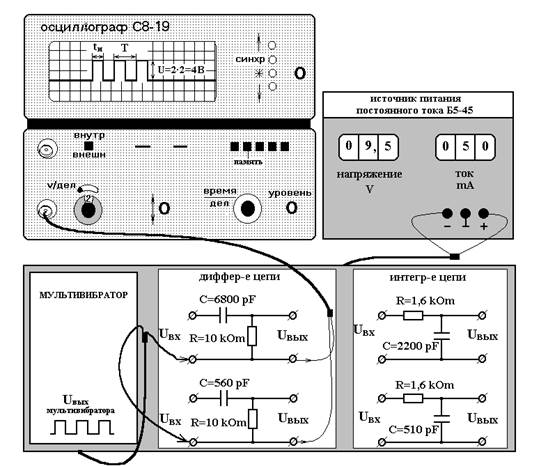
Рис.1. Установка для определения параметров импульсного сигнала

Определение параметров прямоугольного импульса.

Импульс прямоугольной формы необходимо подать на вход осциллографа. Это делают, пользуясь разъемами, минуя дифференцирующую или интегрирующую цепь (рис.1).

По осям осциллографа определите амплитуду, длительность и период повторения импульса. Зная эти параметры рассчитайте скважность и коэффициент заполнения.

Изменение формы прямоугольного импульса дифференцирующей и интегрирующей цепями.

Для изучения работы дифференцирующей цепи необходимо подать на ее вход прямоугольный импульс от мультивибратора, а полученный сигнал с выхода подать на вход осциллографа (рис.2).

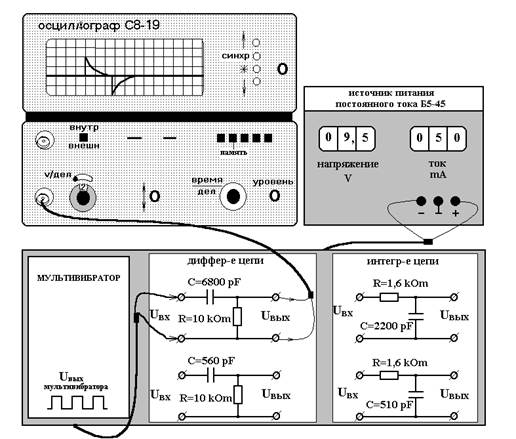
Рис.2. Изучение работы дифференцирующей цепи.

Зарисуйте сигналы, полученные после прохождения первой и второй дифференцирующей цепей и объясните различие в форме полученных сигналов.

То же самое проделайте с интегрирующими цепями.

Оформите отчет по проделанной работе.

.

Свободные электромагнитные колебания

Свободными (собственными) электромагнитными ко­лебаниями называют такие, которые совершаются без внешнего воздействия за счет первона­чально накопленной энергии.

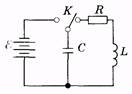Рассмотрим колебательный контур, состоящий из резистора R, катушки индуктивности L и конденсатора С (рис. 14.1); сопротивлением проводов и возможным излучением электромагнитных волн пренебрегаем. Конденсатор ключом К заряжается от источника * , а затем разряжается на резистор и катушку индуктивности. При этом в контуре возникает ЭДС

самоиндукции 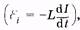, которая, согласно закону Ома, будет Рис. 14.1 равна сумме напряжений на элементах цепи: на резисторе U_R = IR и конденсаторе 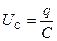. Поэтому запишем

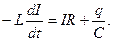(14.1)

Преобразуем это уравнение, поделив все члены на L и учитывая, что 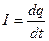и :

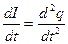(14.2)

Это есть дифференциальное уравнение свободных электроманитных колебаний. Произведя замены:

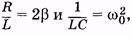(14.3)

получим уравнение

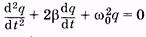(14.4)

Незатухающие колебания. Если контур не содержит резистора (рис. 14.2), то из (14.4) имеем:

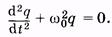(14.5)

Известно, что (14.5) является дифференциальным уравнением гармонического колебания, его решение [см. (5.8)] имеет вид

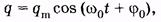(14.6)

где q_m— наибольший (начальный) заряд на обкладках конденсатора, w₀ — круговая частота собственных колебаний (собственная круговая частота) контура, j₀ — начальная фаза.

По гармоническому закону изменяется не только заряд на обкладках конденсатора, но и напряжение, и сила тока в контуре, соответственно:

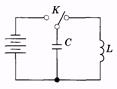Рис. 14.2 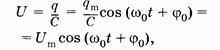(14.7)

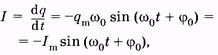(14.8)

где U_m и I_т — амплитуды напряжения и силы тока.

Графики зависимости заряда (напряжения) от времени аналогичны графику зависимости смещения x(t), а график зависимости силы тока от времени — графику скорости u (t) (см. рис. 5.4).

Из (14.3) найдем выражение для периода собственных колебаний (формула Томсона):

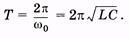(14.9)

Затухающие колебания.При наличии резистора (рис. 14.1) процесс в контуре описывается уравнением (14.4), которое аналогично уравнению (5.19) для механических колебаний. При условии, что затухание не слишком велико, то есть 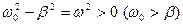находим следующее решение [см. (5.20)]:

(14.10)

График этой функции аналогичен графику на рис. 5.6. Если затухание мало ( ), то w » w₀. В этом случае логарифмический декремент затухания

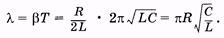(14.11)

Апериодический разряд конденсатора на резистор(силь­ное затухание). При сильном затухании 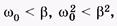или, используя (14.3),

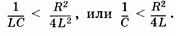(14.12)

Неравенство (14.12) выполняется, в частности, в контуре при отсутствии индуктивности (L ® 0). Для этого случая (разряд кон­денсатора на резистор) из (14.1) имеем

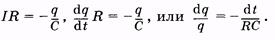(14.13)

Интегрируя последнее уравнение, находим

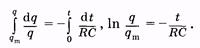(14.14)

Потенцируя второе из выражений (14.14), имеем

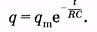(14.15)

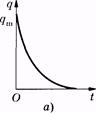
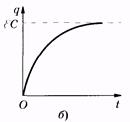
Рис. 14.3

Уравнение (14.15) описывает процесс разрядки конденсатора С на резистор R. При отсутствии индуктивности колебания не воз­никают (рис. 14.3, а). По такому закону изменяется и напряжение на обкладках конденсатора. Теоретически такой процесс, как это следует из (14.15), протекает бесконечно долго, однако принято длительность подобных процессов оценивать временем, в течение которого параметр, характеризующий процесс (в данном случае заряд и напряжение), уменьшится в е раз (постоянная времени,t).

Выражение для постоянной времени можно получить из (14.15), если вместо q подставить 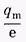, a t заменить на t: 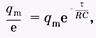откуда для контура с конденсатором и резистором постоянная времени равна

t = RС. (14.16)

Можно показать, что зарядка конденсатора от источника постоянной ЭДС * также происходит по экспоненциальному закону

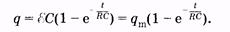(14.17)

График этой зависимости представлен на рис. 14.3,6.