Задачи для подготовки к экзамену
1. Исследовать ряды на сходимость:
1) 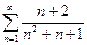 ; 2)
; 2) 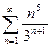 ; 3)
; 3) 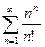 ; 4)
; 4) 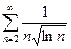 ; 5)
; 5) 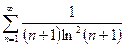 ; 6)
; 6) 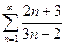 ;
;
7) 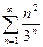 ; 8)
; 8) 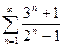 ; 9)
; 9) 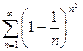 ; 10)
; 10)  ; 11)
; 11)  ; 12)
; 12) 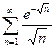 .
.
2. Найти область сходимости степенного ряда:
1) 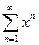 ; 2)
; 2) 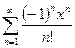 ; 3)
; 3) 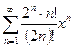 ; 4)
; 4) 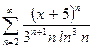 , 5)
, 5) 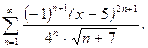
3. Радиус сходимости степенного ряда 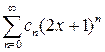 равен 1. Тогда ряд сходится в интервале…
равен 1. Тогда ряд сходится в интервале…
4. Найти разложение в ряд следующих интегралов:
1) 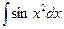 ; 2)
; 2) 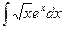 ; 3)
; 3) 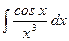 ; 4)
; 4) 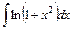 .
.
5. Вычислить:
1) 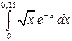 с точностью до 0,001; 3)
с точностью до 0,001; 3) 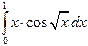 с точностью до 0,001;
с точностью до 0,001;
2) 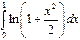 с точностью до 0,001; 4)
с точностью до 0,001; 4) 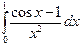 с точностью до 0,001.
с точностью до 0,001.
6. Найти первые шесть членов разложения в ряд решения уравнения 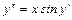 , удовлетворяющего условиям
, удовлетворяющего условиям 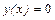 ,
, 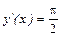 .
.
7. Найти три первых, отличных от нуля членов разложения в степенной ряд функции 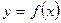 , являющихся решением дифференциального уравнения
, являющихся решением дифференциального уравнения 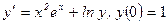 .
.
8. Периодическую функцию 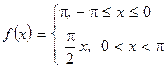 с периодом
с периодом 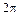 разложить в ряд Фурье.
разложить в ряд Фурье.
9. Среди 25 студентов, из которых 15 девушек, разыгрываются 4 билета, причем каждый может выиграть только один билет. Какова вероятность того, что среди обладателей билетов окажутся: а) 4 девушки; б) 4 юноши; в)3 юноши и 1 девушка.
10. В коробке 10 красных, 3 синих, 7 желтых карандашей. Наудачу из коробки берут одновременно 3 карандаша. Найти вероятность того, что хотя бы два из них одного цвета.
11. Карточки с буквами слова АВТОПОРТРЕТ смешивают и выбирают по одной наудачу без возврата 4 карточки, раскладывая их в порядке появления. Определить вероятность того, что в результате получится слово ПОРТ.
12. Пассажир может прибыть к месту назначения любым из автобусов А, В и С, интервалы движения которых 1 час, 1,5 часа и 2 часа соответственно. Найти вероятность того, что время ожидания не превысит 0,8 часов.
13. Рабочий обслуживает три станка. Вероятность того, что в течение смены потребуют его внимания первый станок, равна 0,7, второй – 0,75, третий – 0,8. Найти вероятность того, что в течение смены потребуют внимания рабочего какие – либо два станка.
14. Оптовая база обслуживает 12 магазинов, от каждого из них заявка на товары на следующий день может поступить с вероятностью 0,3. Найдите наивероятнейшее число заявок на следующий день и вероятность получения базой такого числа заявок.
15. Фарфоровый завод отправил на базу 10000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0001. Найдите вероятность того, что на базу придут ровно 3 повреждённых изделия.
16. На факультете 730 студентов. Вероятность того, что студент не придет на занятия, равна 0,1. Найдите наивероятнейшее число студентов, не явившихся на занятия, и вероятность этого события.
17. Было посажено 400 деревьев. Вероятность того, что отдельное дерево приживется, равна 0,8. Найдите вероятность того, что число прижившихся деревьев больше 300.
18. Предполагается, что 10% открывающихся новых предприятий прекращают свою деятельность в течение года. Какова вероятность того, что из 6 малых предприятий не более двух в течение года прекратят свою деятельность?
19. Производится залп из 6 орудий по некоторому объекту. Вероятность попадания в объект из каждого орудия равна 0,6. Найти вероятность ликвидации объекта, если для этого необходимо не менее 4-х попаданий.
20. Вся продукция цеха проверяется двумя контролёрами, причём первый контролёр проверяет 55% изделий, а второй - остальные. Вероятность того, первый контролёр пропустит нестандартное изделие, равна 0,01, второй – 0,02. Взятое на удачу изделие оказалось нестандартным. Найти вероятность того, что это изделие проверялось вторым контролёром.
21. . Вероятность сбоя в работе телефонной станции равна 0,007. Поступило 1000 вызовов. Определить вероятность того что сбой произошел не менее 3 раз.
22. Одна из случайных величин задана законом распределения
| хi | -1 | ||
| pi | 0,1 | 0,8 | 0,1 |
А другая случайная величина имеет биноминальный закон распределения с параметрами n=2, p=0,6. Составить закон распределения их суммы и найти математическое ожидание этой случайной величины.
23. Случайные величины Х и У независимы и имеют один и тот же закон распределения:
| значения | |||
| pi | 0,2 | 0,3 | 0,5 |
Составить закон распределения случайных величин 2Х и Х+У. Убедиться в том, что 2Х 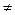 Х+У.
Х+У.
24. Охотник, имеющий 4 патрона, стреляет по дичи до первого попадания или до израсходования всех патронов. Вероятность попадания при первом выстреле равна 0,6, при каждом последующем - уменьшается на 0,1. Необходимо: 1) составить закон распределения случайной величины Х – числа патронов, израсходованных охотником; 2) найти математическое ожидание, дисперсию этой случайной величины.
25. Студент с целью поиска нужной ему книги решил обойти имеющиеся в городе 4 библиотеки. Предполагая, что вероятность наличия нужной студенту книги в библиотеке равна 0,4, составить закон распределения числа библиотек, которые посетит студент. Найти математическое ожидание и дисперсию этой случайной величины.
26. Среди 15 собранных агрегатов 6 нуждаются в дополнительной смазке. Составить закон распределения числа агрегатов, нуждающихся в дополнительной смазке, среди 5 наудачу отобранных из общего числа. Найти математическое ожидание и дисперсию этой случайной величины.
27. Среди 7 изготовленных приборов имеется 3 недостаточно точных. Составить закон распределения случайной величины Х – числа не достаточно точных приборов среди взятых одновременно четырёх приборов. Найти функцию распределения этой случайной величины и построить её график.
28. Имеются 4 ключа, из которых только один подходит к замку. Составить закон распределения числа попыток открыть замок, если испробованный ключ в последующих попытках не участвует. Найти математическое ожидание, дисперсию и моду этой случайной величины.
29. Плотность распределения некоторой непрерывной случайной величины Х имеет вид:
f(x) = 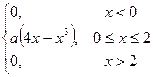 .
.
Найти: a, F(x), M{x}, D{x}, Mo{x}, P(0<X<1). Построить графики f(x) и F(x).
30. Случайная величина Х задана функцией распределения
F(x) = 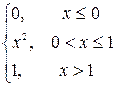
Найти: f(x), M{x}, D{x}, Mo{x}, P(0,5<X<1). Построить графики f(x) и F(x).
31. Случайная величина задана функцией 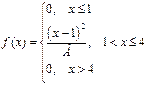 Найти: М(x); D(x), P(3<x<4,5) , построить графики f(X) и F(X).
Найти: М(x); D(x), P(3<x<4,5) , построить графики f(X) и F(X).
32. 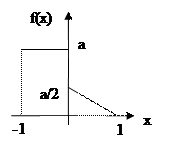 Найти а, f(x), F(x), M(x) и Д(х), если плотность вероятности непрерывной случайной величины X имеет вид:
Найти а, f(x), F(x), M(x) и Д(х), если плотность вероятности непрерывной случайной величины X имеет вид:
33. В таблице приведены результаты измерения роста (в см) случайно отобранных 100 студентов
| Рост | 154-158 | 158-162 | 162-166 | 166-170 | 170-174 | 174-178 | 178-182 |
| Число студентов |
Найти выборочную среднюю и выборочную дисперсию роста обследованных студентов. Найти исправленную выборочную дисперсию. Построить гистограмму относительных частот.
34. По выборке объема n=100 построена гистограмма частот:
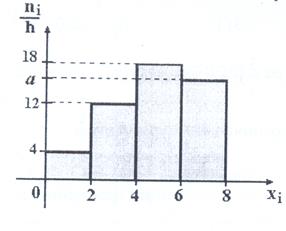
Найти значение а
35. Случайная ошибки измерения детали подчинены нормальному закону с параметром 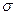 = 20 мм. Найти вероятность того, что измерение детали произведено с ошибкой, не превосходящей по модулю 25 мм.
= 20 мм. Найти вероятность того, что измерение детали произведено с ошибкой, не превосходящей по модулю 25 мм.
36.
37. Произведена выборка объёмом n=100 из большой партии однотипных приборов. Средний срок службы прибора выборки оказался равным 5000 ч. Найти с надёжностью 0,95 доверительный интервал для среднего срока службы прибора во всей партии, если среднее квадратическое отклонение срока службы составляет 40 ч.
38. Найти минимальный объём выборки, при котором с надёжностью 0,975 точность оценки математического ожидания m генеральной совокупности по выборочной средней будет равна 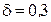 , если известно среднеквадратическое отклонение
, если известно среднеквадратическое отклонение 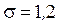 нормально распределённой генеральной совокупности.
нормально распределённой генеральной совокупности.
