Напряжение в любой точке поперечного сечения

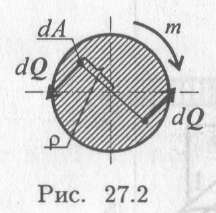
Рассмотрим поперечное сечение круглого бруса. Под действием внешнего момента в каждой точке поперечного сечения возникают силы упругостиdQ(рис. 27.2).

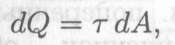
где τ — касательное напряжение;dA — элементарная площадка.

В силу симметрии сечения силыdQ образуют пары (см. лек­цию 26).

Элементарный момент силыdQ относительно центра круга

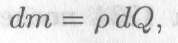
где ρ— расстояние от точки до центра круга.

Суммарный момент сил упругости получаем сложением (инте­грированием) элементарных моментов:

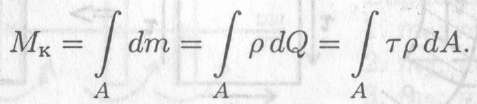
После преобразования получим формулу для определения на­пряжений в точке поперечного сечения:

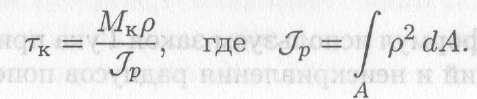
При ρ = 0 τ_к = 0; касательное напряжение при кручении пропорционально расстоянию от точки до центра сечения.

Полученный интегралJ_v (лекция 25) называется полярным мо­ментом инерции сечения.J_v является геометрической характеристи­кой сечения при кручении. Она характеризует сопротивление сече­ния скручиванию.

Анализ полученной формулы дляJ_v показывает, что слои, рас­положенные дальше от центра, испытывают большие напряжения.

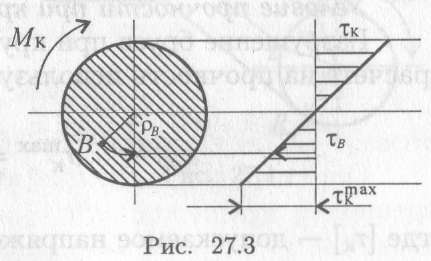
Эпюра распределения касательных напряжений при кручении (рис. 27.3)

М_к — крутящий момент в сечении;

рв — расстояние от точки В до центра;

т_в — напряжение в точке В]

т_mах — максимальное напряже­ние.

Максимальные напряжения при кручении

Из формулы для определения напряжений и эпюры распределе­ния касательных напряжений при кручении видно, что максималь­ные напряжения возникают на поверхности.

Определим максимальное напряжение, учитывая, что ρ_тах= d/2, гдеd — диаметр бруса круглого сечения.

Для круглого сечения полярный момент инерции рассчитывается по формуле (см. лекцию 25).

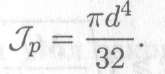
Максимальное напряжение возникает на поверхности, поэтому имеем

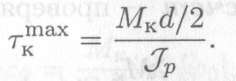
ОбычноJ_P/p_max обозначаютW_p и называют моментом сопротивления при кручении, или полярным моментом сопротивления сечения

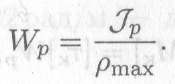
Таким образом, для расчета максимального напряжения на поверхности круглого бруса получаем формулу

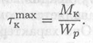
Для круглого сечения

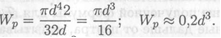
Для кольцевого сечения

Условие прочности при кручении

Разрушение бруса при кручении происходит с поверхности, при расчете на прочность используют условие прочности

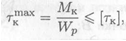
где [τ_к] — допускаемое напряжение кручения.

Виды расчетов на прочность

Существует два вида расчета на прочность.

1. Проектировочный расчет — определяется диаметр бруса (вала) в опасном сечении:

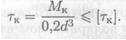
Откуда

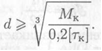
1. Проверочный расчет — проверяется выполнение условия прочности

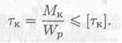
3. Определение нагрузочной способности (максимального крутящего момента)

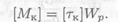
Расчет на жесткость

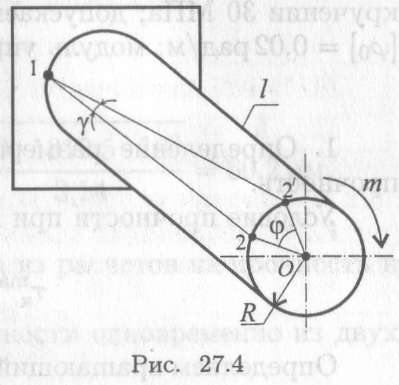
При расчете на жесткость определяется деформация и сравнивается с допускаемой. Рассмотрим деформацию круглого бруса над действием внешней пары сил с моментом т (рис. 27.4).

При кручении деформация оценивается углом закручивания (см. лекцию 26):

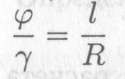
Здесь φ — угол закручивания; γ — угол сдвига; l — длина бруса; R — радиус;R =d/2. Откуда

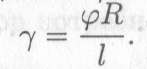
Закон Гука имеет вид τ_к = G_γ. Подставим выражение для γ, получим

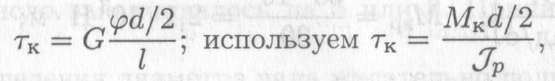
Откуда

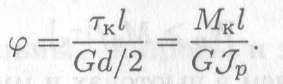
ПроизведениеGJ_P называют жесткостью сечения.

Модуль упругости можно определить какG = 0,4Е. Для сталиG = 0,8 • 10⁵ МПа.

Обычно рассчитывается угол закручивания, приходящийся на один метр длины бруса (вала) φ_o.

Условие жесткости при кручении можно записать в виде

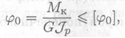
где φ_o — относительный угол закручивания, φ_о = φ/l; [φ_о] ≈ 1град/м = 0,02рад/м — допускаемый относительный угол закручивания.

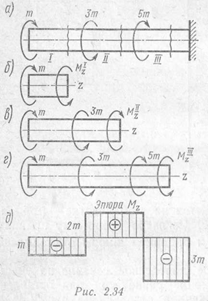
Пример:Для бруса, изображенного на рис. 2.34, а, построить эпюру крутящихмоментов. Из расчетов на прочность и жесткость определить потребный диаметр вала. Материал вала — сталь, допускаемое напряжение при кручении 30 МПа; допускаемый относительный угол закручивания [φ_о] = 0,02рад/м; модуль упругости при сдвиге G = 0,8 * 10⁵ МПа.

Решение

1. Заданный брус имеет три участка I, II,III. Напомним, что границами участков являются сечения, в которых прилажены внешние (скручивающие) моменты.

В данном случае проще, применяя метод сечений, оставлять левую и отбрасывать правую часть бруса — это дает возможность не определять реактивный момент в заделке.

Проводим произвольное поперечное сечение на участке Iи составляем уравнение равновесия для оставлен­ной части бруса, изображенной отдельно на рис. 2.34, 6:

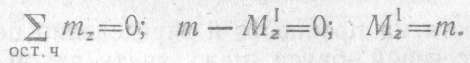
В любом сечении участка I крутящий момент имеет найденное значениеM¹_z = т. Из уравнения равновесия для оставленной части значениеM¹_zполучилось со знаком плюс. Это указывает на то, что выбранное направление M¹_z соответствует действительному.

Эпюра крутящих моментов на этом участке — прямая, параллельная оси абсцисс. Согласно принятому правилу знаков М¹_я отрицателен, и ординаты эпюры откладываем вниз от ее оси.

2. Проводим произвольное поперечное сечение на участке II и составляем уравнение равновесия для оставлен­ной части бруса, изображенной отдельно на рис. 2.34, в:

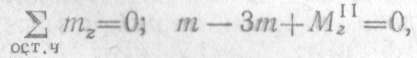
Откуда

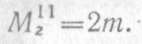
И в этом случае выбранное направление M^II_z соответствует действительному. В любом сечении участка II крутящий момент Mz^II= 2m. Согласно принятому правилу знаков,Mz^II положителен и ординаты эпюры откладываем вверх от ее оси.

3. Проводим произвольное поперечное сечение на участке III и составляем уравнение равновесия для оставленной части бруса, изображенной отдельно на рис. 2.34, г:

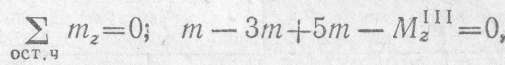
откуда

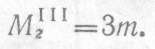
В любом сечении участка IIIMz^III = —Зт.

Эпюра крутящих моментов представлена на рис. 2.34, д.

При нагружении бруса сосредоточенными моментами эпюра всегда имеет такой же характер, как и в рассматриваемом случае: на отдельных участках она ограничена прямыми, параллельными оси абсцисс; в местах при­ложения внешних (скручивающих) моментов получаются скачки на величину этих моментов.

4. Определение размеров поперечного сечения из расчета на прочность.

Условие прочности при кручении:

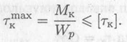
Из условия прочности определяем момент сопротивления вала при кручении

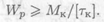
Значения подставляем в ньютонах и мм.

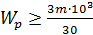мм³

Определяем диаметр вала:

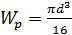; d ;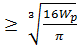

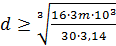
5. Определение размеров поперечного сечения из расчета на жесткость.

Условие жесткости при кручении:

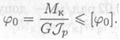
Из условия жесткости определяем момент инерции сечения при кручении:

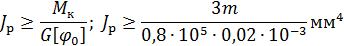
Определяем диаметр вала:

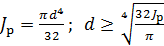мм

6. Выбор потребного диаметра вала из расчетов на прочность и жесткость.

Для обеспечения прочности и жесткости одновременно из двух найденных значений выбираем большее.

Полученное значение следует округлить, используя ряд предпочтительных чисел. Для определения диаметра вала желательно пользоваться стандартным рядом диаметров

Задание:

1. Определить значения крутящих моментов

2. Построить эпюры крутящих моментов

3. Определить диаметр вала из условий прочности и жёсткости

4. Материал вала — сталь, допускаемое напряжение при кручении 30 МПа; допускаемый относительный угол закручивания [φо] = 0,02рад/м; модуль упругости при сдвиге G = 0,8∙105 МПа.

М1

М2

М3

М1 М2

М3

М1

М2

М3

М1 М2

М3

М1

М2

М3

a b

c

e

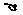
М1 М2М3

М3

М1

М2

М3

М1 М2

М3

М1

М2

М3

М1М2 М2

a b

c

e

М1

М2

М3

М1 М2

М3

М1

М2

М3

М1 М2

М3

М1

М2

М3

a b

c

e

М3

М1

М2

М3

М1 М2

М3

М1

М2

М3

М1М2 М2

a b

c

e

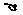
М1 М2М3

№ Варианта	М1,Н∙м	М2, Н∙м	М3, Н∙м

Контрольные вопросы.

1. Какие деформации возникают при кручении?

2. Какие гипотезы выполняются при деформации кручения?

3. Изменяются ли длина и диаметр вала после скручивания?

4. Какие внутренние силовые факторы возникают при кручении?

Содержание отчета

13. Схема вала

14. Решение

15. Эпюры крутящих моментов

16. Ответы на контрольные вопросы

17. Вывод.

Практическая работа № 7

Тема:Построение эпюр поперечных сил и изгибающих моментов.

Цель: Научиться находить изгибающие моменты и напряжения и производить расчеты на прочность и жесткость при изгибе.

Теоретическая часть:

При чистом изгибе в сечении возникает только один внутренний силовой фактор — изгибающий момент.

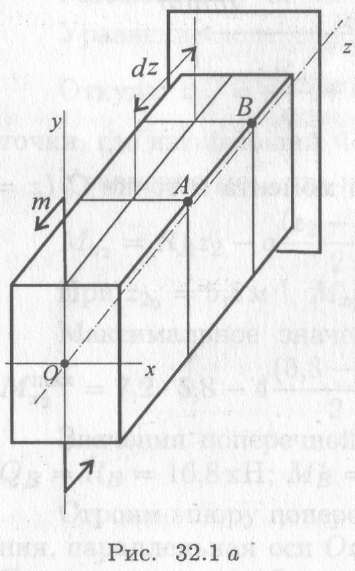
Рассмотрим деформацию бруса, нагруженного внешней парой сил с моментом т (рис. 32.1а)_.

При чистом изгибе выполняются гипотезы плоских сечений и ненадавливаемости слоев.

Сечения бруса, плоские и пер­пендикулярные продольной оси, после деформации остаются плоскими и пер­пендикулярными продольной оси.

Продольные волокна не давят друг на друга, поэтому слои испытывают простое растяжение или сжатие.

Действуют только нормальные на­пряжения.

Поперечные размеры сечений не меняются.

Продольная ось бруса после деформации изгиба искривляется и образует дугу окружности радиуса ρ (рис. 32.1б). Материал подчиняется закону Гука.

Можно заметить, что слои, расположенные выше продольной оси, растянуты, расположенные ниже оси — сжаты (рис. 32.1б). Так как деформации по высоте сечения меняются непрерывно, имеется слой, в котором нормальные напряжения σ равны нулю; такой слой называют нейтральным слоем (НС). Доказано, нейтральный слой проходит через центр тяжести сечения; ρ — радиус кривизны нейтрального слоя.

Рассмотрим деформа­цию слоя, расположенного на расстоянии у от ней­тральной оси (участок АВ, рис. 32.1).

Длина участка до дефор­мации равна длине нейтральной оси:

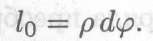
Абсолютное удлинение слоя

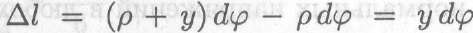(рис. 32.1б).

Относительное удлинение

Относительное удлинение прямо пропорционально расстоянию слоя до нейтральной оси.

Используем закон Гука при растяжении: σ = Еε.

Получим зависимость нормального напряжения при изгибе от положения слоя:

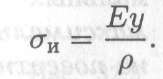
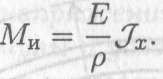
Откуда: 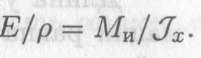Ранее получено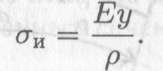

После ряда преобразований получим формулу для определения нормальных напряжений в любом слое поперечного сечения бруса:

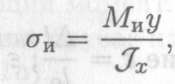
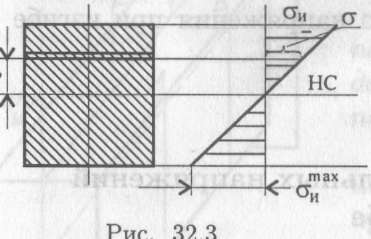гдеJ_x — геометрическая характеристика сечения при изгибе.

Эпюра распределения нормальных напряжений при изгибе изображена на рис. 32.3.

По эпюре распределения нормальных напряжений видно, что максимальное напряжение возникает на поверхности.

Подставим в формулу напряжения значение у = y_max

Получим

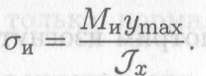
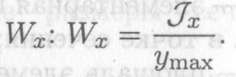
Отношение принято обозначать

Эта величина называется моментом сопротивления сечения при изгибе, или осевым моментом сопротивления. Размерность — мм³.

W_x характеризует влияние формы и размеров сечения на проч­ность при изгибе. Напряжение на поверхности

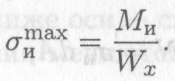
Определим рациональные сечения при изгибе, для этого срав­ним моменты сопротивления простейших сечений.

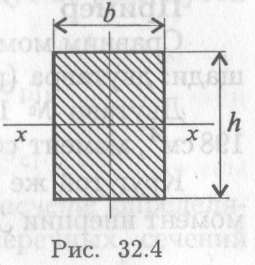
Осевой момент инерции прямоугольника (рис. 32.4, вывод формулы в лекции 25) ра­вен

Осевой момент сопротивления прямоуголь­ника

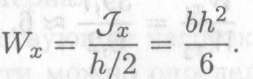
Сравним сопротивление изгибу двух прямоугольных сечений (рис. 32.5).

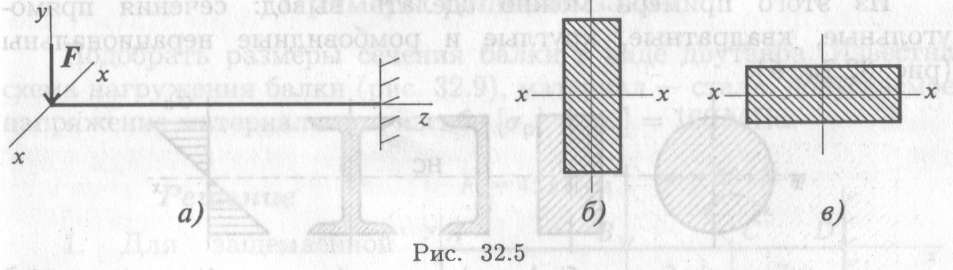
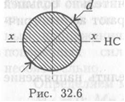
Вариант на рис. 32.5, б обладает большим сопротивлением изгибу при прочих равных условиях.

Осевой момент инерции круга (рис. 32.6) равен

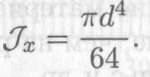
Осевой момент сопротивления круга

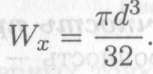
Все необходимые расчетные данные (площади, моменты инер­ции и сопротивления) стандартных сечений приводятся в таблицах стандартов (Приложение 1).

Для материалов, одинаково работающих на растяжение и сжа­тие, выбирают сечения, симметричные относительно оси, вокруг ко­торой совершается изгиб (рис. 32.7).