Системы массового обслуживания (СМО)

В парикмахерский салон приходит в среднем 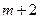клиента в час (т.е. интенсивность 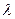поступления заявок в систему равна 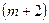/час), а среднее время обслуживания одного клиента равно 1/ 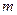часов. Содержание одного рабочего места обходится в 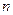тысяч рублей за 1 час, а доход от обслуживания одного клиента составляет 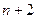тысяч рублей в час.

15.2.1. Найти относительную пропускную способность СМО 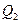(т.е. вероятность того, что поступившая заявка будет обслужена) и абсолютную пропускную способность СМО 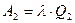(число заявок, обслуживаемых за 1 час), если салон обслуживает два мастера.

15.2.2. Найти доход 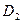, полученный за 1 час работы двух мастеров.

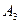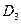15.2.3. Найти аналогичные характеристики СМО , и , когда салон обслуживают три мастера, и определить, выгодно ли принять на работу третьего мастера с точки зрения общего дохода, полученного за 1 час работы салона.

Задача межотраслевого баланса.

Три отрасли промышленности I, II и III являются производителями и в то же время потребителями некоторой продукции. Их взаимосвязь определяет матрица А коэффициентов прямых затрат

,

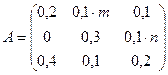в которой число 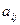, стоящее на пересечении 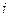-ой строки и 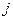-го столбца равно 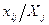, где 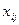– поток средств производства из 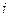-ой отрасли в 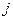-ую, а 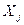– валовой объем продукции 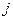-ой отрасли (все объемы продукции выражаются в единицах стоимости).

Задан также вектор 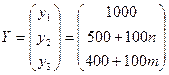объемов конечной продукции.

15.3.1. Составить уравнение межотраслевого баланса.

15.3.2. Решить систему уравнений межотраслевого баланса, то есть найти объемы валовой продукции каждой отрасли 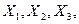обеспечивающие потребности всех отраслей и изготовление конечной продукции Y. (Расчеты рекомендуется производить с точностью до двух знаков после запятой)

15.3.3. Составить таблицу Х потоков средств производства .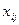

15.3.4. Определить общие доходы каждой отрасли .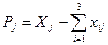

15.3.5. Результаты расчетов оформить в виде таблицы межотраслевого баланса:

потребляющие отрасли отрасли производящие	I	II	III	конечный продукт	валовой продукт
I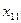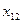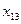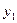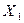
II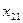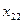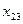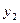
III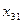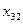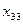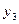
общий доход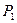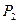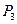
валовой продукт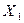

15.3.6. Найти матрицу коэффициентов полных затрат по формуле 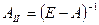, где Е – единичная матрица размера .

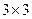Дискретная математика.

Двоичная система счисления.

16.1.1. Записать число 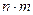в двоичной системе счисления.

Например: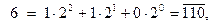

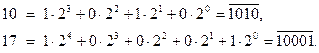
16.1.2. Определить четырехзначное двоичное число 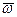своего задания. Для этого необходимо взять последние 4 цифры полученного в задаче 16.1.1. двоичного числа. Если в нем меньше четырех цифр, то слева нужно дописать нули.

Так: ,

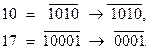
Логика высказываний.

Пусть 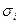принимает значения 0 либо 1 ( 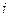= 1, 2, 3, 4). Положим

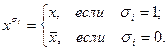
По четырехзначному двоичному числу 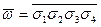, полученному в задаче 16.1.2, составьте формулу логики высказываний

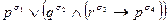
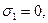
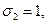
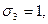
для своего задания. Так, например, двоичному числу 0110 (где 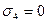) соответствует формула 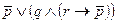, а двоичному числу 1010 - формула 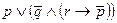. Для полученной формулы:

16.2.1. Найти таблицу истинности.

16.2.2. Определить, эквивалентны ли она и формула .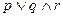

16.2.3. Найти совершенную дизъюнктивную нормальную форму и совершенную конъюнктивную нормальную форму:

а) табличным методом, б) непосредственным преобразованием.

16.2.4 Составить минимальную релейно-контактную схему, приведя формулу к минимальной дизъюнктивной форме.

Краткое содержание (программа) курса

Линейная алгебра.

Матрицы, действия над ними. Определители, их свойства и вычисление. Обратная матрица. Системы линейных уравнений, условие их совместности. Формулы Крамера, метод Гаусса и матричный способ решения систем. Линейный оператор. Собственные векторы и собственные значения линейных операторов.

Аналитичеcкая геометрия.

Простейшие задачи аналитической геометрии (расстояние между точками, деление отрезка в заданном отношении). Прямая на плоскости, различные виды ее уравнений, угол между прямыми. Расстояние от точки до прямой. Геометрический смысл линейных уравнений и неравенств. Кривые второго порядка, их канонические уравнения.

Векторы, линейные операции над ними. Координаты вектора, его длина, направляющие косинусы. Скалярное, векторное и смешанное произведения векторов, условия их перпендикулярности, коллинеарности, компланарности.

Плоскость в пространстве, ее уравнения, угол между плоскостями, расстояние от точки до плоскости. Прямая в пространстве, ее общие и канонические уравнения. Угол между прямой и плоскостью.