Б) общее и частное решения ДУ: , .

Решение.

Тип ДУ первого порядка устанавливают по форме его записи.

1а) Данное уравнение является дифференциальным уравнением с разделяющимися переменными, так как его можно записать в виде

.

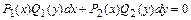Действительно, осуществив в исходном уравнении замену 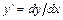и умножив его затем на 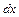, получим: 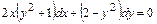, т.е. уравнение с разделяющимися переменными.

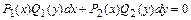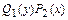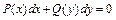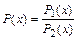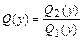Нахождение общего решения уравнения , путём деления обеих его частей на , сводится к интегрированию уравнения с разделёнными переменными , где , , общее решение которого записывается в виде .

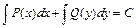Разделим обе части уравнения 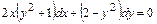на множитель 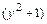, получим ДУ с разделёнными переменными: .

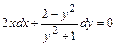Общее решение последнего уравнения найдём интегрированием каждого слагаемого по своей переменной и запишем в ви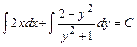де:

, где 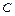- произвольная постоянная.

Общее решение дифференциального уравнения первого порядка должно обязательно содержать одну произвольную постоянную.

Вычислим интегралы (с точностью до постоянного слагаемого):

,

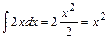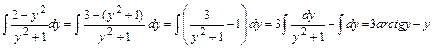Тогда общее решение дифференциального уравнения запишется в виде:

.

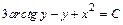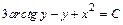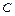Ответ: , где - произвольная постоянная.

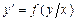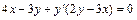
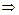
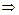
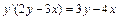
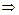
2а) Данное уравнение является однородным дифференциальным уравнением первого порядка, так как его можно записать в виде . Действительно, выполнив преобразования: 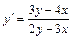, получим .

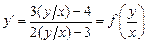При выполнении преобразований однородного ДУ первого порядка к виду 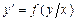следует учесть, что .

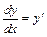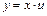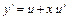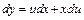Нахождение общего решения однородного ДУ первого порядка с помощью подстановки , или , где 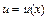- новая неизвестная функция, сводится к нахождению общего решения ДУ с разделяющимися переменными относительно функции 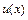с последующей заменой .

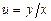С помощью подстановки 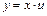, 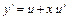уравнение 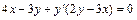или 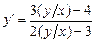приведём к ДУ с разделяющимися переменными 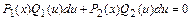относительно новой неизвестной функции 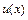. Получим: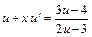

.

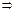
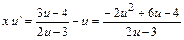
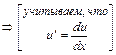
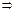
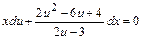Последнее уравнение есть уравнение с разделяющимися переменными. Сведём его, разделив обе части уравнения на множитель 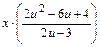к уравнению с разделёнными переменными. Получим: .

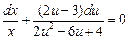Общее решение последнего уравнения найдём интегрированием каждого слагаемого по своей переменной и запишем в ви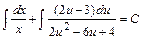де:

, где 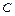- произвольная постоянная.

Вычислим интегралы (с точностью до постоянного слагаемого):

;

.

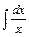
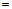
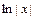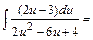
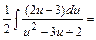
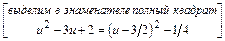
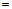
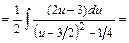
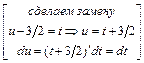
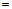
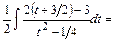
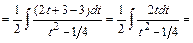
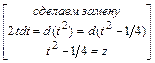
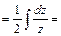
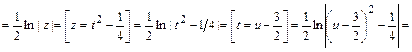
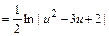Тогда общее решение последнего дифференциального уравнения запишется в виде: 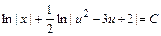или, используя свойства логарифмов, в виде: 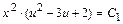, где 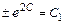- новая произвольная постоянная.

Теперь в найденном решении вернёмся к старой неизвестной функции 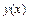, выполнив обратную замену 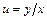. В итоге получим:

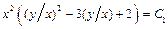или .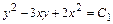

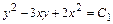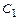Ответ: , где - произвольная постоянная.

б)Данное уравнение является линейным дифференциальным уравнением (ЛДУ) первого порядка, так как его можно записать в ви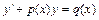де , где , .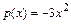

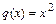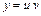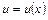Сначала найдем общее решение линейного ДУ первого порядка. Его ищем в виде , где и 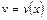- новые неизвестные функции.

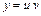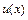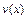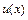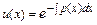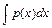Общее решение ЛДУ 1-го порядка находится с помощью подстановки , где , - новые неизвестные функции. Одну из них, например , находят в виде , где - какая-нибудь первообразная для функции 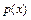, тогда другую неизвестную функцию 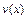находят в виде общего решения ДУ: 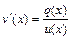. В итоге будет найдено и общее решение исходного уравнения в виде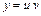

Частное решение ДУ, удовлетворяющее начальному условию 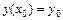получают из общего решения данного уравнения при конкретном значении произвольной постоянной 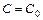. Находят 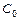как решение уравнения, получаемого подстановкой в общее решение начального условия.

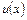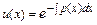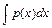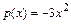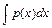
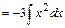
Функцию найдём в виде , где - какая-нибудь первообразная для функции . Вычислив интеграл, получим 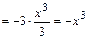. Тогда .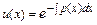

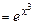Простейшим ДУ первого порядка называется уравнение вида 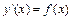. Общее решение такого уравнения находится интегрированием и записывается в виде .

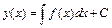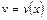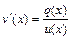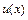
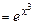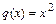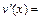
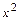
Функцию найдём как общее решение ДУ: , где , . Данное уравнение 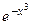является простейшим ДУ первого порядка. Его общее решение найдём интегрированием и запишем в виде 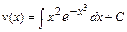. Вычислив интеграл (с точностью до постоянной), получим: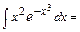

.

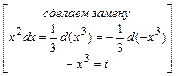
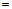
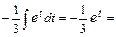
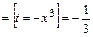
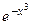Таким образом .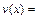

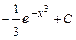Тогда общее решение исходного уравнения запишется в виде:

.

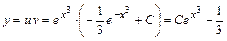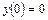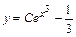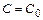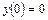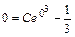
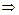
Теперь найдём частное решение, удовлетворяющее начальному условию .Его получим из общего решения при конкретном значении произвольной постоянной , которое найдём из уравнения, полученного подстановкой начального условия в общее решение. В результате получим: 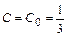. Тогда частное решение исходного дифференциального уравнения, удовлетворяющее начальному условию 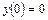, запишется в виде: .

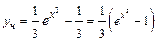Ответ: 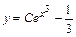- общее решение; 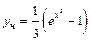частное решение.

141-150.Требуется найти:

а)общеерешениепростейшего ДУ 2-ого порядка ;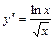

б)общее и частное решения однородного линейного ДУ 2-ого порядка с постоянными коэффициентами: , , ;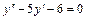

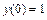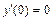в) общее решение линейного ДУ 2-ого порядка с постоянными коэффициентами и правой частью специального вида: .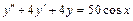

Решение а).

Общее решение простейшего ДУ второго порядка 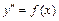находят, выполняя последовательно два интегрирования, и записывают в виде:

.

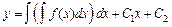Общее решение дифференциального уравнения второго порядка должно обязательно содержать две разные произвольные постоянные.

Данное уравнение дважды проинтегрируем. После первого интегрирования получим: 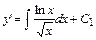. Интеграл вычислим (с точностью до постоянного слагаемого) методом интегрирования по частям. Получим:

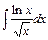
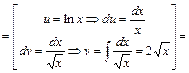
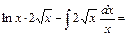
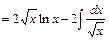
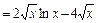. Тогда .

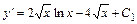После второго интегрирования получим: .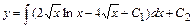

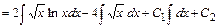Вычислим интегралы (с точностью до постоянного слагаемого). Получим:

;

; .

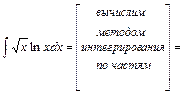
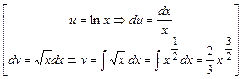
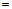
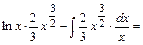
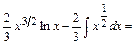
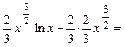
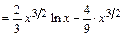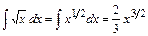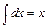Тогда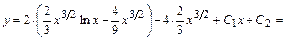

.

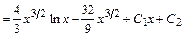Ответ: .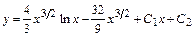

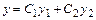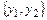Решение б).Сначала найдём общее решение ДУ в виде: , где - фундаментальная система его частных решений.

Общее решение однородного линейного ДУ второго порядка с постоянными коэффициентами 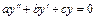имеет вид 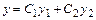, где 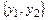- фундаментальная система его частных решений; 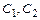-произвольные постоянные.

Фундаментальная система решений 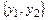строится на основе характера корней характеристического уравнения 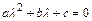. А именно:

1) если 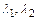- пара различных действительных корней характеристического уравнения, то ФСР имеет вид ;

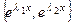2) если 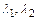- пара одинаковых 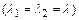действительных корней, то ФСР имеет вид ;

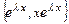3) если 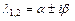- пара комплексно-сопряжённых корней, то ФСР имеет вид .

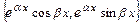Корни характеристического уравнения 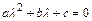, являющегося квадратным, находят на множестве комплексных чисел по формулам:

1) если дискриминант уравнения 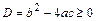, то ;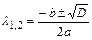

2) если дискриминант уравнения 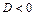, то .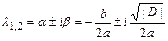

Для нахождения ФСР, составим характеристическое уравнение 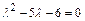для данного дифференциального уравнения и найдём его корни на множестве комплексных чисел. Так как дискриминант 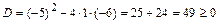, то 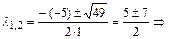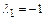, , 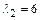т.е. характеристическое уравнение имеет два различных действительных корня. Следовательно, ФСР имеет вид .

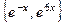Тогда общее решение данного ДУ запишется в виде: .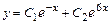

Теперь найдём частное решение данного ДУ, удовлетворяющее начальным условиям: 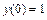, 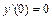. Для этого сначала найдём производную 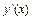общего решения: 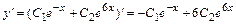. Затем подставим начальные данные в выражения для общего решения и его производной, получим систему линейных алгебраических уравнений для определения значений произвольных постоянных 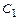и :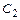

.

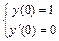
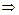
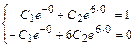
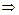
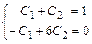Решив систему, найдём: 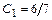, 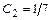. Тогда частное решение данного ДУ запишется в виде: .

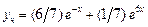Ответ: ; .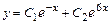

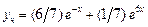Решение в).

Общее решение неоднородного ЛДУ 2-го порядка 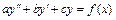имеет вид 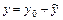, где 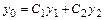- общее решение соответствующего однородного уравнения, 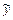- какое-нибудь частное решение данного неоднородного уравнения.

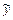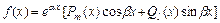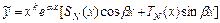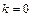Частное решение уравнения с правой частью специального вида ищется методом неопределённых коэффициентов в виде , где , если число 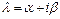не является корнем характеристического уравнения, и 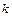равно кратности корня 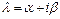в противном случае; 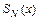и 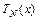- полные многочлены степени 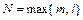с неопределёнными коэффициентами. Примерами полных многочленов с неопределёнными коэффициентами степени 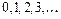соответственно являются: 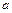, , 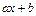, ,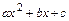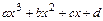…. Для нахождения коэффициентов многочленов 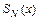и 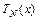, надо подставить решение 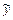в неоднородное дифференциальное уравнение и приравнять коэффициенты при подобных членах в левой и правой частях полученного равенства. В результате получим систему уравнений, решив которую, найдём значения коэффициентов.

Общее решение данного ДУ найдём в ви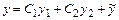де: , где 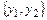- фундаментальная система частных решений соответствующего ему однородного ДУ: 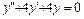; 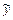- какое-нибудь частное решение данного неоднородного дифференциального уравнения.

Сначала найдём ФСР 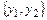соответствующего однородного ДУ 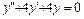. Для этого составим характеристическое уравнение 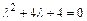для данного однородного дифференциального уравнения и найдём его корни на множестве комплексных чисел. Так как дискриминант 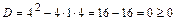, то 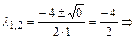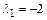, , 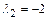т.е. характеристическое уравнение имеет два одинаковых действительных корня. Следовательно, ФСР имеет вид .

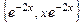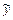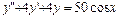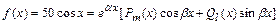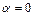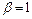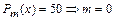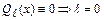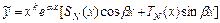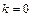Затем найдём частное решение неоднородного уравнения ,имеющегоправую часть специального вида , где , , , . Частное решение найдём в виде , где , если число 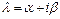не является корнем характеристического уравнения, и 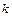равно кратности корня 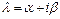в противном случае; 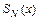и 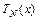- полные многочлены степени 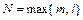с неопределёнными коэффициентами. В данном случае: число 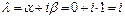не является корнем характеристического уравнения, поэтому 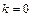; 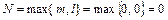, поэтому 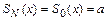, , 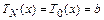где 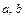- неизвестные постоянные, подлежащие определению. Таким образом, частное решение с неизвестными постоянными запишется в виде:

.

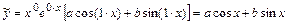Для определения значений постоянных 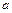и 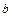, найдём производные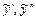

и подставим выражения для 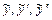вместо 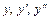в неоднородное уравнение 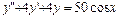.Учитывая, что:

, ,

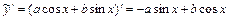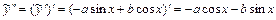получим: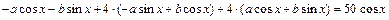

.

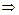
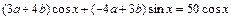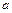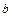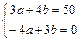Приравняв, в правой и левой части полученного равенства, постоянные коэффициенты, стоящие при одинаковых функциях, получим систему линейных алгебраических уравнений относительно неизвестных и : . Решив систему, найдём: 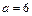, 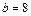. Частное решение 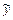запишется тогда в виде: .

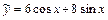Теперь запишем общее решение исходного уравнения в виде:

.

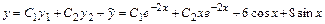Ответ: .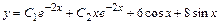

Раздел V. Теория вероятностей и математическая статистика.

151-160. Требуется найти вероятности указанных событий, используя

классическое определение вероятности:

а)Бросаются два игральных кубика. Найти вероятность того, что сумма очков на выпавших гранях – четная, причем на грани хотя бы одного из кубиков появится шестерка.

б) В урне находятся 5 черных и 6 белых шаров. Случайным образом из урны вынимают 4 шара. Найти вероятности того, что среди вынутых шаров окажутся: «2 белых шара»; «не более одного белого шара»; «хотя бы один белый шар».

При классическом определении вероятность случайного события 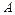определяется равенством: 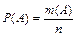, где 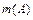- число элементарных (далее неделимых и взаимно исключающих друг друга) исходов эксперимента, благоприятных появлению события 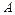; 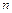- общее число равновозможных элементарных исходов эксперимента. Равновозможность элементарных исходов обеспечивается такими условиями проведения эксперимента (опыта, испытания), при выполнении которых можно считать, что ни один из исходов не является объективно более возможным, чем другие.

Если событие 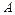определяется словами «хотя бы один…», то непосредственное нахождение 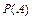по формуле классического определения вероятности приводит обычно к громоздким вычислениям. Проще сначала найти вероятность события 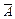, противоположного событию 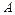и определяемого словами «ни один…», а затем, используя формулу для вероятностей противоположных событий: 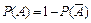, вычислить вероятность искомого события.

Для нахождения вероятности события по формуле 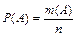необходимо:

1) Рассмотреть событие 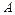, вероятность которого следует найти.

2) Правильно определить, что является в данном испытании элементарным исходом.

3) Найти общее число 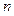элементарных исходов, предварительно выписав их все непосредственно. Если выписать все элементарные исходы не представляется возможным из-за их чрезмерного количества, то при подсчете их числа используют правила и формулы комбинаторики.

4) Установить какое число 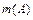элементарных исходов данного испытания благоприятствуют появлению события .

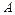Решение.

а) Рассмотрим событие 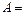{сумма очков на выпавших гранях – четная, причем на грани хотя бы одного из кубиков появится шестерка}.

Элементарными исходами данного испытания (подбрасывание двух игральных кубиков) являются всевозможные комбинации очков: 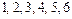, которые могут появиться на верхних гранях двух кубиков.

Общее число элементарных исходов 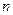данного испытания найдём, используя правило умножения комбинаторики.

Пусть 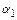, 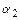– действия из некоторого конечного множества действий.

Правило умножения. Если действие 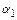можно выполнить 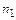способами и, после каждого такого выполнения, действие 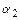можно выполнить 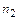способами, то последовательное выполнение пары действи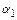й и 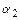можно осуществить 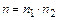способами.

На каждом игральном кубике 6 граней, поэтому возможны шесть исходов бросания каждого из них. Если испытание представить в виде последовательно выполняемых подбрасываний кубиков, то первое подбрасывание можно выполнить 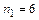способами, второе подбрасывание - 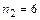способами, тогда последовательно выполняемое подбрасывание двух кубиков можно осуществить 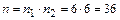способами.

Общее число элементарных исходов 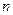можно найти и, выписав непосредственно все возможные исходы испытания:

(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)

(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)

(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)

(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)

(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)

(6,1) (6,2) (6,3) (6,4) (6,5) (6,6).

Теперь найдём число элементарных исходов 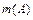данного испытания, благоприятных событию 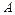, выписав их непосредственно. Такими исходами, очевидно, являются: (2,6); (4,6); (6,2); (6,4); (6,6). Их число .

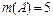Тогда искомая вероятность .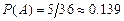

Ответ: .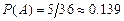

б) Рассмотрим события: 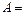{среди четырёх вынутых шаров - 2 белых}, 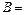{среди четырёх вынутых шаров – не более одного белого шара}, 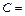{среди четырёх вынутых шаров - хотя бы один белый шар}.

Элементарными исходами данного испытания (случайное вынимание четырех шаров) являются всевозможные комбинации по 4 шара из находящихся в урне 11 шаров.

Для подсчёта общего числа элементарных исходов 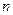данного испытания и чисел 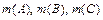элементарных исходов, благоприятных событиям 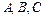, используем правила и формулы комбинаторики.

Пусть 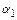, 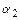– действия из некоторого конечного множества действий.

Правило сложения. Если действие 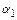можно выполнить 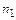способами, действие 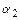- другими 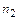способами, отличными от первых 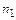, то выполнение одного из действий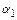: или , или 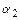(но не двух одновременно) можно осуществить 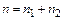способами.

Сочетаниями из 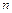элементов по 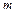называются всевозможные комбинации элементов, отличающиеся друг от друга только составом элементов. Они рассматриваются как элементарные исходы эксперимента, состоящего в одновременном неупорядоченном выборе без возвращения 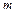элементов из 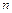различных элементов, а их общее число 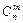определяется формулой:

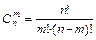, где , .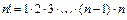

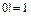Общее число элементарных исходов 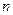данного испытания, очевидно, равно числу всевозможных неупорядоченных комбинаций по 4 шара из находящихся в урне 11 шаров, т.е. числу сочетаний 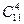. Тогда:

.

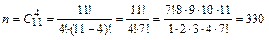Подсчитаем теперь число элементарных исходов 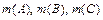благоприятных событиям 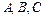, соответственно.

Событие 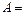{среди четырёх вынутых шаров - 2 белых} означает, что среди вынутых шаров – «2 белых и 2 черных шара». Следовательно, благоприятными событию 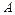являются всевозможные комбинации по 4 шара (два белых и два черных шара) из находящихся в урне 11 шаров. Их число 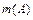найдём, используя правило умножения комбинаторики. Представим для этого выбор четырёх шаров в виде двух последовательно выполняемых действий: сначала выбор двух белых шаров из имеющихся в урне 6 белых шаров и затем выбор двух чёрных шаров из имеющихся в урне 5 чёрных шаров. Получим: 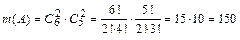. Тогда: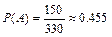

Событие 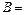{среди четырёх вынутых шаров – не более одного белого шара} означает, что среди вынутых шаров - или «один белый и три черных шара», или «четыре чёрных шара». Следовательно, благоприятствующими событию 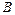являются всевозможные комбинации по 4 шара (один белый и три черных или четыре черных шара) из находящихся в урне 11 шаров. Их число 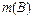найдём, используя правила сложения и умножения комбинаторики. Сначала, используя правило умножения комбинаторики, найдём число способов выбрать один белый и три черных шара. Получим 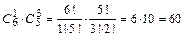. Затем, используя правило умножения комбинаторики, найдём число способов выбрать 4 чёрных шара. Получим 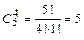. Теперь, используя правило сложения комбинаторики, найдём число 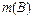способов выбрать или один белый и три чёрных шара, или четыре чёрных шара. Получим 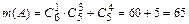. Тогда .

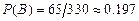Событие 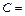{среди четырёх вынутых шаров-хотя бы один белый шар} определяется словами «хотя бы один…». Прямое решение задачи, учитывая, что событие 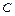означает, среди вынутых шаров: или «один белый и три черных шара», или «два белых и два черных шара», или «три белых и один черный шар», или «четыре белых шара», приводит к громоздким вычислениям. Поэтому сначала найдём вероятность противоположного события 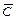={среди вынутых четырёх шаров нет ни одного белого шара, т.е. все шары – черные}. Получим 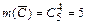, тогда 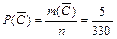. Затем по формуле 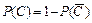найдём вероятность искомого события: .

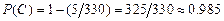Ответ: ; ; .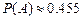

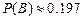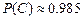161-170.Требуется найти вероятности указанных событий, используя:

а) формулы сложения и умножения вероятностей;

б) формулу Бернулли;

а) Экзаменационная сессия состоит из трёх экзаменов. Студент оценивает свои шансы успешно сдать экзамены следующим образом: вероятность сдать первый экзамен - 0.8, второй – 0.9, третий – 0.7. Найти вероятности того, что студентом будут успешно сданы: «все три экзамена», «по крайней мере два экзамена», «хотя бы один экзамен». Предполагается, что сдача экзаменов – независимые события.

б) В урне 15 белых и 10 черных шаров. Из урны вынимают подряд 5 шаров, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из пяти вынутых шаров окажется не более двух белых.

Решение а).

Сложным называют событие, наблюдаемое в эксперименте и выражаемое через другие наблюдаемые в том же эксперименте события с помощью допустимых алгебраических операций над событиями.

Вероятность осуществления того или иного сложного события вычисляется с помощью формул умножения вероятностей:

1) , ;

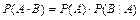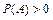2) 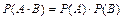(для независимых событий)

и формул сложения вероятностей:

3) ;

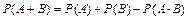4) 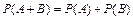(для несовместных событий).

События 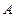и 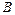называют несовместными, если 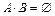. Несовместными событиями являются, например, элементарные исходы эксперимента.

События 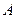и 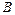, называются независимыми, если выполняется равенство 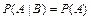, в противном случае они называются зависимыми. Часто, независимость событий определяется условиями проведения эксперимента.

Для решения задач с использованием формул сложения и умножения вероятностей следует:

1) рассмотреть «сложное» событие, вероятность которого нужно вычислить;

2) выразить «сложное» событие, посредством допустимых алгебраических операций, через наблюдаемые в том же эксперименте «простые» события, вероятности которых известны или легко определяются из условий задачи, например, по формуле классического определения вероятности;

3) вычислить вероятность «сложного» события с помощью формул сложения и умножения вероятностей, учитывая зависимость или независимость, совместность или несовместность составляющих его событий.

Рассмотрим «сложные» события: 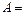{студент успешно сдаст все три экзамена}, 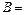{студент успешно сдаст по крайней мере два экзамена из трёх}, 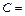{студент успешно сдаст хотя бы один экзамен из трех}.

Выразим сначала «сложные» события 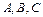через «простые» события: 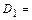{студент успешно сдаст первый экзамен}, 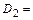{студент успешно сдаст второй экзамен}, 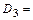{студент успешно сдаст третий экзамен}, вероятности которых известны и равны: 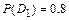, , 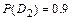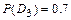. Затем вычислим вероятности 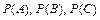, используя формулы сложения и умножения вероятностей, учитывая при этом зависимость и независимость, совместность и несовместность составляющих событий.

Событие 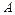представим в виде 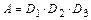. Тогда, учитывая независимость событий 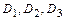, по формуле умножения вероятностей для независимых событий получим: .

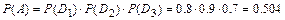Событие 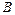означает, очевидно, что студент сдаст или все три экзамена, или только любые два экзамена из трёх. Следовательно:

+ + ,

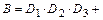
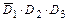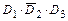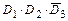где 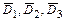- события, противоположные к событиям 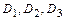: 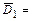{студент не сдаст первый экзамен}, 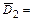{студент не сдаст второй экзамен}, 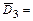{студент не сдаст третий экзамен}, вероятности которых:

, , .

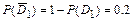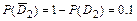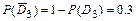Тогда, учитывая несовместность событий 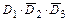, , 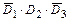, 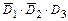являющихся элементарными исходами эксперимента (экзаменационной сессии), а также независимость событий 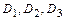, , 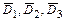используя формулы сложения (для несовместных событий) и умножения вероятностей (для независимых событий), получим:

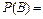
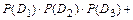
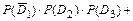
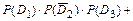
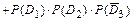
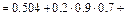
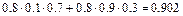
Событие 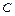, определяемое словами «хотя бы один», означает, что студент сдаст или все три экзамена, или только любые два экзамена из трёх, или только любой один экзамен из трёх. Прямое вычисление вероятности данного события приводит к громоздким вычислениям. Поэтому, сначала найдём вероятность противоположного события 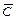={студент не сдаст ни одного экзамена}, представляемого в виде 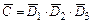. Учитывая независимость событий 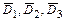, по формуле умножения вероятностей для независимых событий получим: .

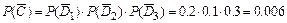Тогда .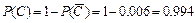

Ответ: , , .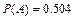

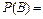
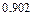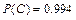Решение б).

Схемой Бернулли называют последовательность испытаний, удовлетворяющую условиям: 1) результатом каждого испытания является один из двух возможных исходов: «успех» (появление некоторого события 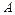) и «неудача»; 2) испытания являются независимыми, т.е. вероятность «успеха» в каждом следующем испытании не зависит от результатов предыдущих испытаний; 3) вероятность «успеха» во всех испытаниях одинакова и равна .

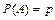Вероятность 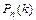того, что в 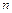испытаниях по схеме Бернулли произойдёт ровно 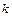«успехов», определяется формулой Бернулли:

, .

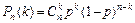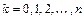Следствием формулы Бернулли является формула: 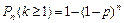- вероятность того, что в 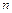испытаниях по схеме Бернулли «успех» наступит хотя бы один раз.

Для решения задач с использованием формулы Бернулли следует:

1) установить, что эксперимент представляет собой схему Бернулли (вероятности событий, связанных с таким экспериментом, всегда можно выразить через вероятности 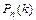, вычисляемые по формуле Бернулли);

2) рассмотреть событие 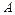, которое может наступить или не наступить в каждом испытании и вычислить его вероятность ;

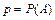3) рассмотреть событие 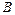, вероятность которого нужно найти и которое состоит в том, что событие 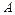в данном эксперименте появляется определённое число раз;