Метод наименьших квадратов. Метод наименьших квадратов (МНК) был сформулирован Лежандром и Гауссом раньше, чем метод регрессии

Метод наименьших квадратов (МНК) был сформулирован Лежандром и Гауссом раньше, чем метод регрессии. Он применяется как независимый метод аппроксимации результатов экспериментальных исследований для произвольно принятой модели. В частности, модель можно искать методом проб. Наилучшей признается та модель, для которой сумма квадратов погрешностей наименьшая. Для этого используются, в частности, такие итерационные процедуры, которые позволяют не изменять вычисленные ранее коэффициенты при смене модели. Чаще всего модели строят, используя многочлены и ортогональные ряды: полиномы Лежандра, Чебышева, функции Лагерра, Чебышева, Эрмита, Уэлша, Хаара.

Так, например, для результатов измерения скорости обезуглероживания в функции времени отыскивалась возможность аппроксимации их многочленом Грама в виде

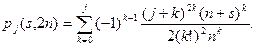(3.133)

Здесь п — нормированные значения независимой переменной для равноудаленных точек -п, -п+1, ..., 0, 1, ..., n; s— текущая переменная, s = [(x — х₀)/d] — п; х₀ — начальная точка независимой переменной; d=const — шаг пробных измерений; j — степень многочлена. Моделью служит многочлен

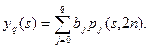(3.134)

Результатом идентификации и подгонки является следующий ряд моделей с погрешностями М:

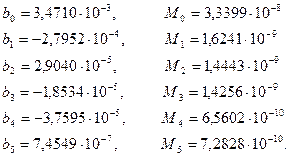
Погрешность вычислялась по формуле

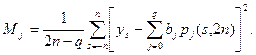(3.135)

Наилучшее приближение дает многочлен четвертой степени. Идея МНК изложена в предыдущем разделе.

МНК и МВНК, как и другие статистические методы, не позволяют вскрыть систематические погрешности. Если погрешности имеют нормальное распределение, то, исследуя сумму квадратов М (3.135), можно выявить, выполняются ли принятые допущения.

Другие методы

Применение вычислительных машин для расчетов стимулировало разработку множества методов идентификации. Их общий принцип обычно состоит в определении таких значений коэффициентов, которые удовлетворяют критерию оптимальности.

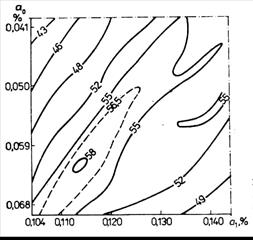
Рис. 3.22. Результаты исследований модели системы для измерения содержания углерода. 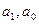— параметры модели (3.123)

Так, например, для погрешностей можно сформулировать следующие требования:

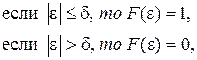(3.136)

а также

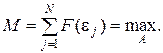(3.137)

Погрешность ε определяется как в МНК, а именно:

e = y-f(x), (3.138)

где х, у — реализации, j = 1, ..., N.

Функцию f и коэффициенты можно подбирать произвольно, а построенная модель будет наилучшей в смысле критерия (3.137) среди исследованных моделей. Критерий (3.137) труден для аналитических расчетов, зато относительно прост для расчетов на ЭВМ. В примере ИС для измерения скорости обезуглероживания исследована линейная модель (3.123) при использовании критерия (3.137). Результаты исследований представлены на рис. 3.22. В принципе для определения значений коэффициентов при идентификации модели используют метод пробных измерений, отыскания области Монте-Карло, меток планирования эксперимента либо поиска оптимума. Достоинством этих методов является возможность применения стандартных машинных программ. К наиболее известным относится метод стохастической аппроксимации, в котором минимизируется математическое ожидание квадрата погрешностей:

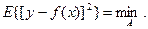(3.139)

Достоинствами этого метода являются рекуррентная форма алгоритма и малый объем вычислений.

Контрольные вопросы к разделу 3

1. Какого типа бывают элементы измерительных систем? По какому признаку они различаются?

2. Каковы отличительные особенности моделирования в метрологии?

3. Какие задачи моделирования вы знаете?

4. Какие преобразования происходят в измерительной системе?

5. Какие факторы учитываются при моделировании измерительной системы?

6. В чем заключается процедура градуировки? Каково ее назначение?

7. По каким признакам классифицируют модели характеристик измерительных систем?

8. Что такое статическая модель?

9. Какие способы линеаризации нелинейных характеристик измерительных систем вы знаете?

10. Чем динамическая модель отличается от статической?

11. Каково назначение модулятора амплитуды?

12. Опишите принцип действия модулятора частоты.

13. Какие отличительные особенности имеют модели с дискретным временем?

14. Для чего в цифровом вольтметре с двойным интегрированием применяется второе интегрирование?

15. Какого рода факторы учитывают при моделировании источников погрешностей?

16. Чем явления молекулярного характера отличаются от процессов старения и износа в плане их влияния на погрешность измерительных систем?

17. Какие этапы моделирования нелинейных элементов измерительных систем вы знаете?

18. Перечислите виды нестационарных источников погрешностей.

19. В чем отличие нестационарного элемента и нестационарного источника погрешностей?

20. Что такое дисперсия погрешности?

21. Чем отличаются распределения погрешностей магнитоэлектрического и электромагнитного приборов?

22. Какие параметры модели определяются при корреляционном анализе?

23. Чем отличается регрессия первого рода от регрессии второго рода?

24. В чем заключается метод наименьших квадратов?

25. Каковы отличительные особенности метода средневзвешенных наименьших квадратов?

26. Является ли метод наименьших квадратов регрессионным методом? Это одно и то же?

27. В чем отличительные особенности численных методов моделирования? В каких случаях применение таких моделей выгодно?

Библиографический список

1. Теория измерений для инженеров / Я. Пиотровский. М.: Машиностроение, 1989

2. Основы теории статических измерений / Э.И. Цветков. М.: Машиностроение, 1986.

3. Оценка погрешностей результатов измерений / П.В. Новицкий. М.: Машиностроение, 1985.

4. Модели в науке и технике /Я.Г. Науймин. Л.: Наука, 1984.

5. Теоретические основы информационно-измерительной техники / П.П. Орнатский. М.: Издательство Стандартов, 1985.

6. Моделирование операций контроля и управления точностью / М.И. Коченов. М.: Машиностроение, 1984.

7. Основы теории и расчета информационно-измерительных систем / М.И. Коченов. М.: Машиностроение, 1980.

Учебное издание

ОБЩАЯ ТЕОРИЯ ИЗМЕРЕНИЙ

Автор-составитель Бирюков Дмитрий Юрьевич

Редактор Н.П.Кубыщенко

Верстка Д.Ю.Бирюкова

ИД №06263 от 12.11.2001 г.

___________________________________________________________

Подписано в печать 30.06.2006 Формат 60x84 1/16

Бумага типографская Офсетная печать Усл.печ.л. 5,81

Уч.-изд.л. 5,8 Тираж 50 экз. Заказ Цена "С"

^{___________________________}

Редакционно-издательский отдел ГОУ ВПО УГТУ-УПИ

620002, Екатеринбург, ул. Мира, 19

Ризография НИЧ ГОУ ВПО УГТУ-УПИ,

620002, Екатеринбург, ул. Мира, 19

[1] Этим термином обобщенно определяются все процедуры передачи меры сверху вниз по ступеням иерархии средств измерения. В таком случае частной процедуре эталонирования при передаче меры от предыдущего уров­ня к последующему по иерархии средств измерения соответствует термин «калибровка».

[2] От лат. propagare — распространять; этот термин используется в био­логии для обозначения понятия «размножение». — Прим, перев.

[3] Это значит, что в качестве номинальной принимается мера эталона, скорректированная по (2.4).

[4] При контрольном сравнении двух эталонов (2.9б) получаем

[5] Значение g₂ измеряется другим независимым методом.

[6] Это составляющие , и ,порождаемые вторичным эталоном.

[7] Обычно отношение мер двух эталонов выражается натуральным чис­лом. Возможны два пути:

1. Используется метод сравнения (компаративный) со значением К=n либо k=min (метод совпадения), т. е, где m,n — натуральные числа.

2. Первичный эталон сравнивается с n одинаковыми вторичными эталонами, для которых , либо m одинаковых первичных эталонов сравниваются с одним вторичным эталоном, для которых .

При этом пользуются физически реализованными операциями разделения или объединения состояний величины. Эти операции реализованы для значительного числа физических величин в соответствии со свойствами метрических шкал.

[8] Международная практическая температурная шкала.

[9] Модели первой категории называются сигнальными моделями, а второй — моделями значений (величин).

[10] В случае модуляции амплитуды импульсов модулированный описывается уравнением u=A

[11] Здесь использованы следующие обозначения в модели и в условиях сравнения:

y=F₀(x)=b₁f₁(x)+b₂f₂(x)+…+b_i f_i (x), что согласуется с моделью (3.13).

[12] Как показано выше, определяющими их входными величинами являются конструктивные параметры, обозначенные здесь символом x.

[13] Для непрерывных нестационарных процессов моделью функции корреляции обычно служит функция, подобная показанным на рис. 3.17.

[14] МНК можно использовать и без условия = const, но получаемые при этом оценки будут менее эффективны (об этом см. ниже).