Релятивистская динамика

Закон для силы остается прежним:

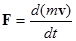
Изменяется выражение для импульса:

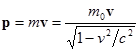
В этом выражении масса тела m является переменной величиной и зависит от скорости. Такую массу называют релятивисткой массой. А массу неподвижной частицы m₀ называют массой покоя.

Все чаще используется также следующая трактовка выражения для импульса. Масса частицы остается постоянной и равной массе покоя, а изменяется ход времени в системе отсчета, связанной с движущейся частицей:

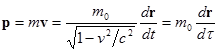, где dt - промежуток собственного времени частицы (отсчитываемого по часам, движущимся в месте с частицей), соответствующий перемещению dr.

Актуальным является вопрос - что будет, если на тело неограниченно долго действует постоянная сила с точки зрения неподвижного наблюдателя? В механике Ньютона скорость тела будет равномерно нарастать и может при этом превысить скорость света. В релятивистской механике равномерно нарастает полная величина импульса. Однако, когда скорость тела приблизится к скорости света, рост импульса происходит не за счет увеличения скорости, которая практически насыщается, а за счет безграничного увеличения массы тела (или допустимо считать, что масса тела остается постоянной, а безгранично замедляется собственное время движущегося тела).

При не слишком больших скоростях можно разложить в ряд (по формуле бинома Ньютона) выражение для релятивистской массы и ограничиться первыми двумя членами ряда:

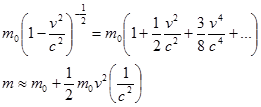
Во втором слагаемом последнего выражения можно узнать кинетическую энергию тела, деленную на квадрат скорости света. Можно записать:

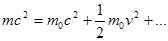
Эйнштейн осмыслил это уравнение, как выражение для энергии тела:

mc² - полная энергия тела;

m₀c² - энергия покоящегося тела;

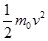- обычная кинетическая энергия тела.

Предположение Эйнштейна о том, что энергия тела всегда равна mc², согласуется с формулой для релятивистской массы. Действительно, из основного уравнения динамики следует, что скорость изменения энергии тела (т.е. мощность) равняется произведению силы на скорость

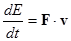
Отсюда:

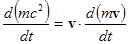
Мы хотим решить это уравнение относительно m. Для этого помножим обе части на 2m:

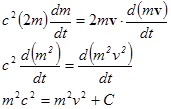
Константу интегрирования С находим из начального условия:

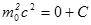
В результате уравнение приобретает вид:

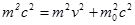
Выражаем в явном виде m:

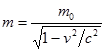
Эта формула для релятивистской массы необходима для того, чтобы полная энергия тела была эквивалентна массе и выражалась как mc².

Вывод об эквивалентности массы и энергии прекрасно подтвердился в опытах по аннигиляции материи - превращению вещества в энергию. Электрон с позитроном могут взаимодействовать в покое, имея каждый массу покоя m₀. При сближении они исчезают, а вместо них излучаются два g-луча, каждый опять с энергией m₀c². Этот опыт прямо сообщает нам о величине энергии, связанной с существованием массы покоя у частицы.