Метод начальных параметров
Для того, чтобы на практике воспользоваться решением (8.6):
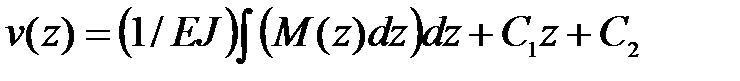 ,
, 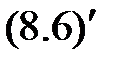
нужно, во-первых, определить постоянные интегрирования 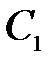 и
и 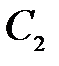 , а во-вторых, вычислить входящий сюда интеграл. Аналогичное замечание касается и выражения (8.9).
, а во-вторых, вычислить входящий сюда интеграл. Аналогичное замечание касается и выражения (8.9).
Решение первой задачи упрощается, если выразить константы через начальные параметры 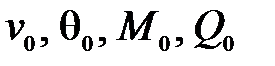 , представляющие собой значения соответствующих функций в начальном сечении балки - на ее левом конце.
, представляющие собой значения соответствующих функций в начальном сечении балки - на ее левом конце.
Подставляя  в (8.5) и (8.6) получим:
в (8.5) и (8.6) получим:
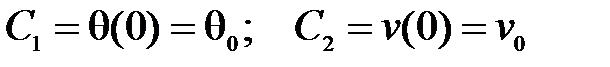 (8.10)
(8.10)
Аналогично выражаются эти константы и в формуле (8.9).
Переходя к вычислению интеграла, входящего в (8.6), вспомним, что для построения эпюр  и
и 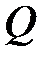 мы разбивали балку на отдельные участки и для каждого из них функция
мы разбивали балку на отдельные участки и для каждого из них функция 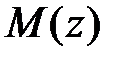 имела различный вид. При таком подходе на каждом участке интеграл нужно вычислять отдельно, а затем стыковать полученные кривые, решая для nучастков балки систему 2n уравнений.
имела различный вид. При таком подходе на каждом участке интеграл нужно вычислять отдельно, а затем стыковать полученные кривые, решая для nучастков балки систему 2n уравнений.
Гораздо продуктивнее идея, которая заключается в том, чтобы представить функцию 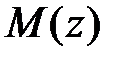 в виде, едином для всех ее участков.
в виде, едином для всех ее участков.
В самом общем случае нагрузку, приложенную к произвольной балке,можно представить так, как показано на рис. 8.2. Будем придерживаться следующих правил при вычислении изгибающего момента в ее сечении:
1) начало отсчета выбирается на левом конце балки, всегда рассматривается часть балки, расположенная слева от сечения;
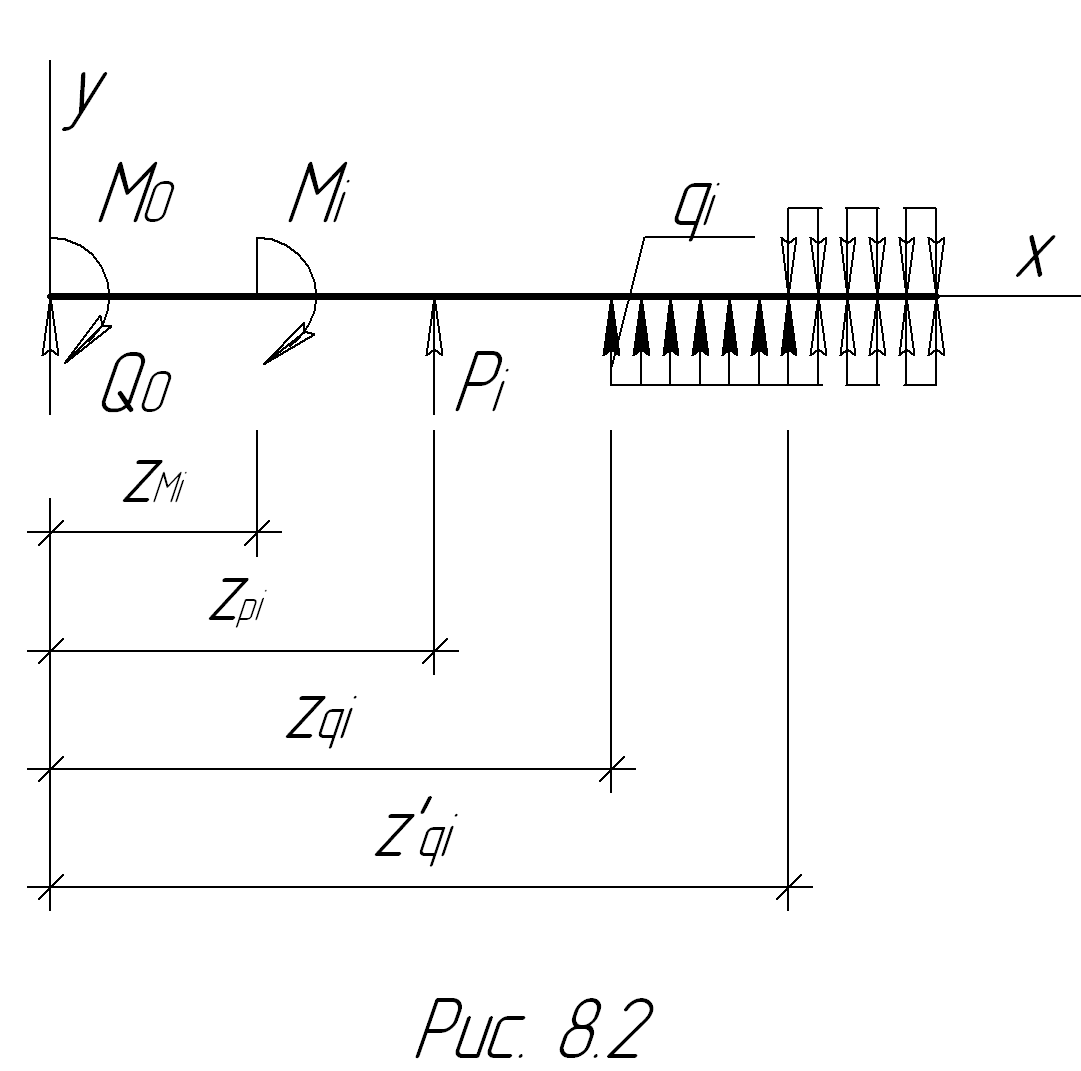
2) положительные 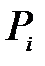 и
и 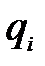 направлены по оси
направлены по оси 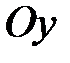 , а моменты
, а моменты 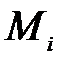 - по ходу часовой стрелки, как показано на рисунке;
- по ходу часовой стрелки, как показано на рисунке;
3) распределенная нагрузка 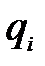 , приложенная на участке
, приложенная на участке 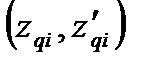 , заменяется той же нагрузкой, продолженной до конца балки, и соответствующей компенсирующей нагрузкой.
, заменяется той же нагрузкой, продолженной до конца балки, и соответствующей компенсирующей нагрузкой.
При этих условиях изгибающий момент в поперечном сечении любого участка балки можно представить в виде:
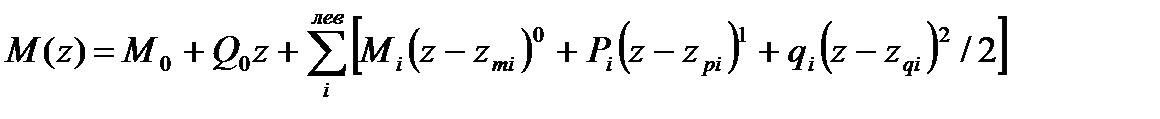 , (8.11)
, (8.11)
где суммирование распространяется на нагрузку, расположенную слева от рассматриваемого сечения.
В самом деле, для участков балки на рис.8.2 функция 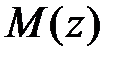 равна:
равна:
1) 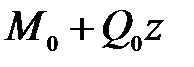 (0£ z < zmi),
(0£ z < zmi),
2) 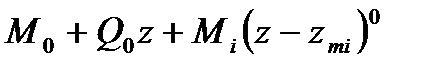 (zmi £ z < zpi),
(zmi £ z < zpi),
3) 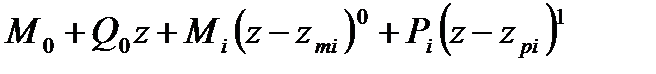 (zpi £ z < zqi)
(zpi £ z < zqi)
и так далее.
Интегрируя дважды последние выражения, на тех же участках балки для 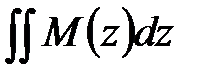 соответственно получим:
соответственно получим:
1) 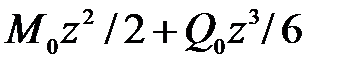 ,
,
2) 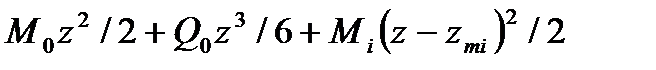 ,
,
3) 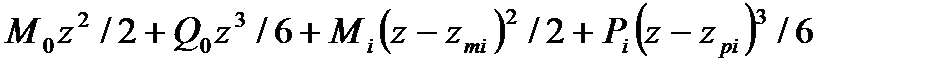 .
.
Таким образом, подставляя (8.11) в (8.6), интегрируя дважды и собирая вместе коэффициенты с начальными параметрами, получим,
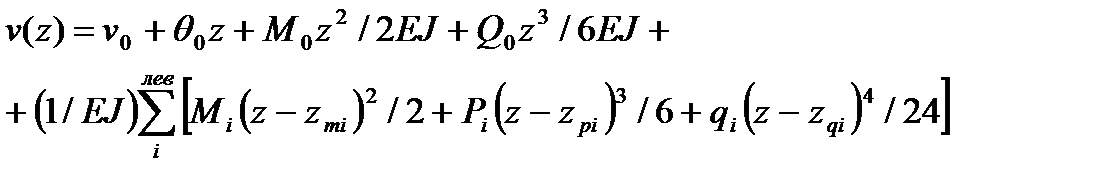 (8.12)
(8.12)
Это выражение носит название универсального уравнения изогнутой оси балки.
Из четырех входящих сюда начальных параметров два всегда известны, а два других можно найти из краевых условий или уравнений статики.
ПРИМЕЧАНИЕ. Термин «универсальное» в отношении выражения (8.12) означает, что его форма не зависит от вида нагрузки и числа загруженных участков балки.
Отметим, что это уравнение справедливо для любых типов балок - как статически определимых, так и статически неопределимых.
Примеры расчета
Рассмотрим примеры определения перемещений в балках с помощью уравнения (8.12). Во всех случаях жесткость балки будем считать заданной.
Пример 8.1.Определить максимальный прогиб балки (рис.8.3а).
Решение. Три из четырех начальных параметров для нашей балки известны: 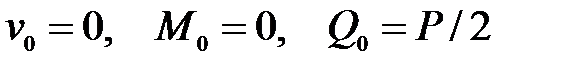 , поэтому уравнение (8.12) примет вид:
, поэтому уравнение (8.12) примет вид:
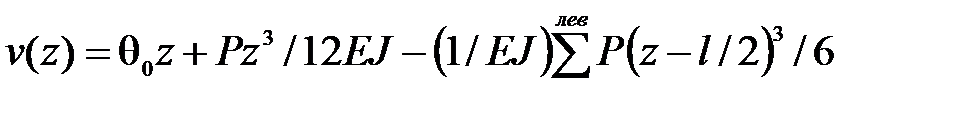 (а)
(а)
Последний параметр  найдем из краевого условия
найдем из краевого условия  :
:
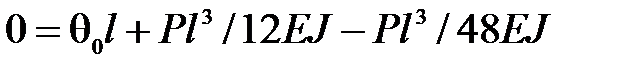 ,
,
откуда
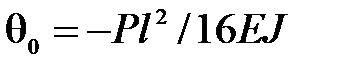 .
.
Подставляя найденные значения  в (а), находим максимальный по модулю прогиб в середине балки:
в (а), находим максимальный по модулю прогиб в середине балки:
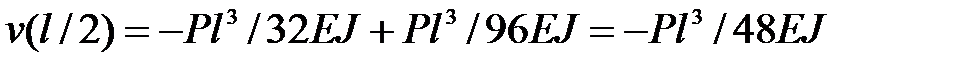 . ·
. ·
| Pl2/16EI |
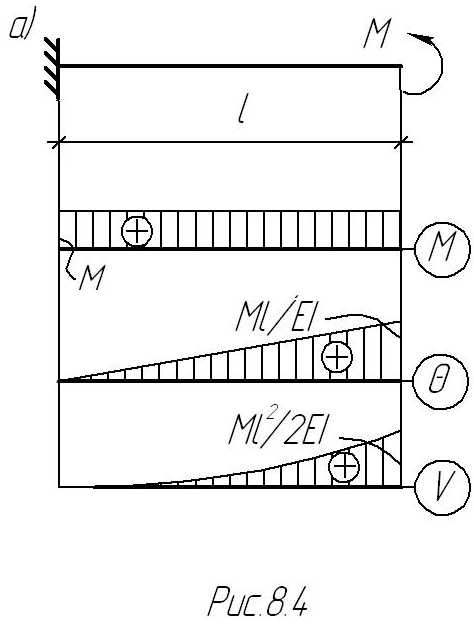
Пример 8.2.Для заданной балки построить эпюры прогибов и углов поворота сечений (рис.8.4а).
Решение. Нагрузка внутри области, занятой балкой  отсутствует, поэтому уравнение (8.12) примет вид:
отсутствует, поэтому уравнение (8.12) примет вид:
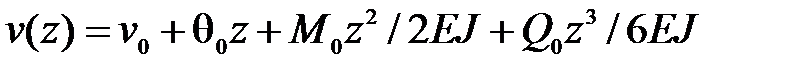 .
.
Два начальных параметра балки известны из условий закрепления: 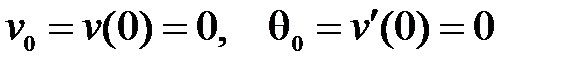 , а два других - равны опорным реакциям:
, а два других - равны опорным реакциям: 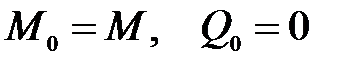 , откуда искомое уравнение:
, откуда искомое уравнение:
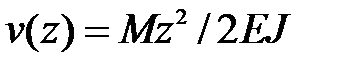 .
.
Дифференцируя, получим:
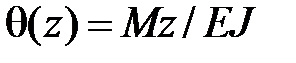 . ·
. ·
Пример 8.3.Найти максимальные прогибы балки (рис.8.5а).
Решение. Как и в предыдущем примере
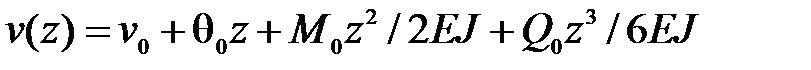 ,
,
где 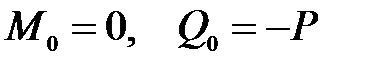 . Для определения неизвестных начальных параметров
. Для определения неизвестных начальных параметров 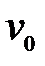 и
и 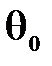 нужно воспользоваться краевыми условиями:
нужно воспользоваться краевыми условиями: 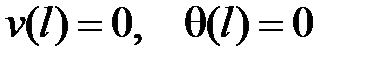 . Решая полученную систему уравнений:
. Решая полученную систему уравнений:
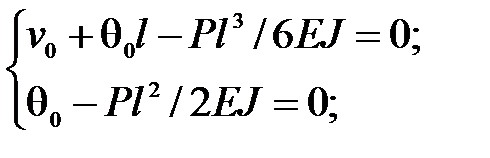
найдем: 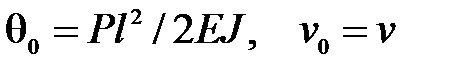 max
max 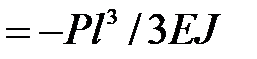 .
.
| Pl2/2EI |
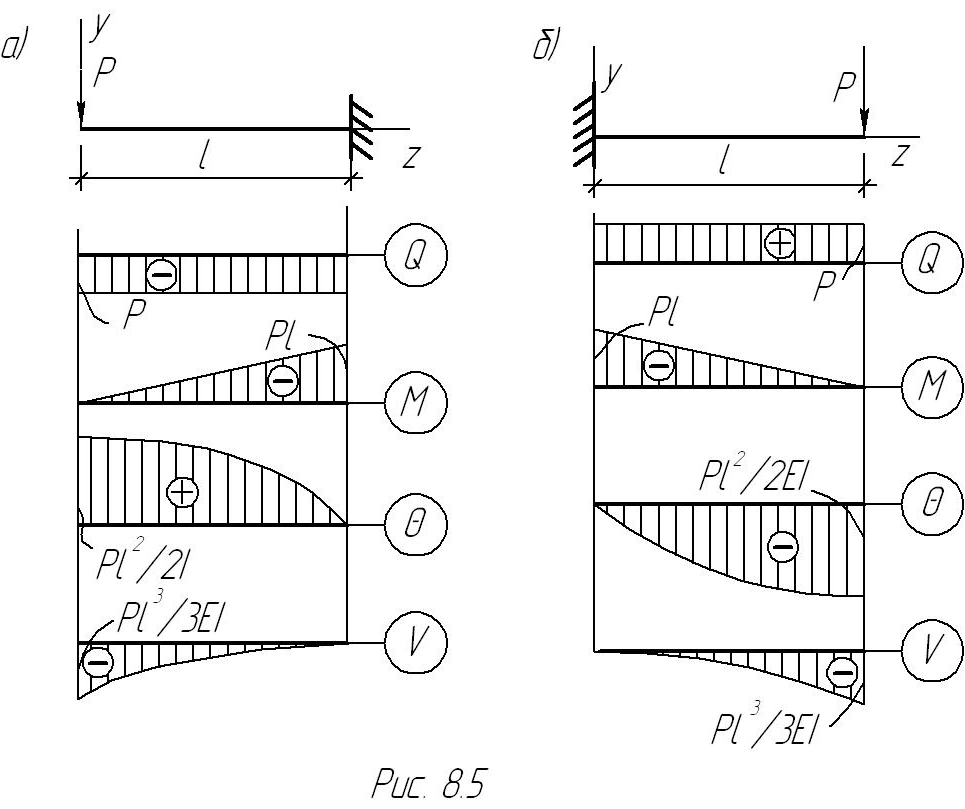
Решение задачи можно упростить, если заданную балку заменить симметрично расположенной (рис.8.5б). Для последней балки все четыре начальных параметра известны: 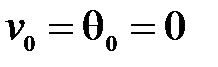 ,
, 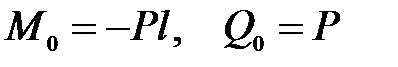 и уравнение (а) примет вид:
и уравнение (а) примет вид:
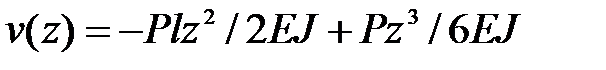 ,
,
откуда
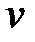 max
max 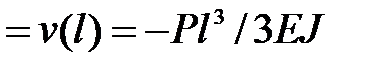 .
.
Отметим, что все эпюры в заданной балке (рис.8.5а) получаются из эпюр, показанных на рис. 8.5б путем продолжения последних в область отрицательных значений  как симметричных (четных) - v и M либо обратно симметричных (нечетных) -
как симметричных (четных) - v и M либо обратно симметричных (нечетных) -  и Q. ·
и Q. ·
Пример 8.4.Определить прогиб и угол поворота сечения в середине пролета балки (рис.8.6а).
Решение. Три начальных параметра известны либо из условий закрепления ( 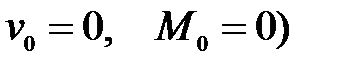 , либо из уравнений равновесия
, либо из уравнений равновесия 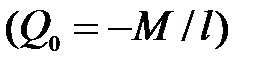 , поэтому уравнение (8.12) имеет вид:
, поэтому уравнение (8.12) имеет вид:
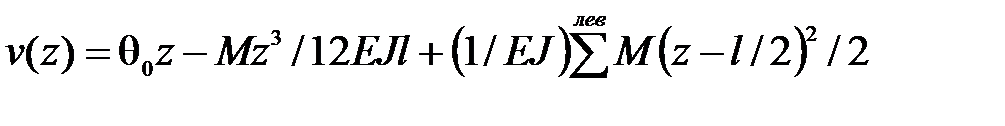 (а)
(а)
| ql2/8 |
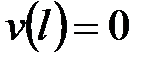 , найдем
, найдем 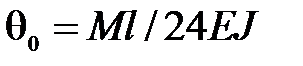 , после чего определим искомый прогиб:
, после чего определим искомый прогиб: 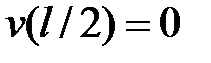 . Дифференцируя (а), получим:
. Дифференцируя (а), получим: 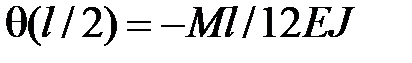 . ·
. · 
Пример 8.5.Построить эпюры Q и М (рис.8.7а).
Решение. Из условий закрепления левого конца балки 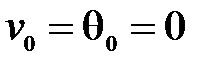 , поэтому
, поэтому
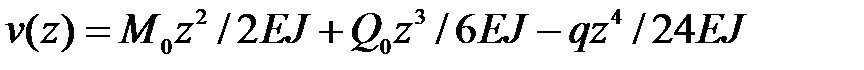 (а)
(а)
Дифференцируя дважды и умножая результат на  , получим:
, получим:
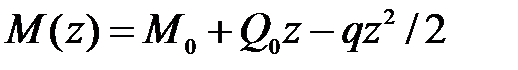 (б)
(б)
Подставляя (а) и (б) в краевые условия: 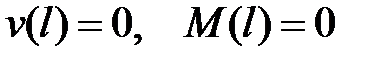 и решая полученную систему уравнений:
и решая полученную систему уравнений:
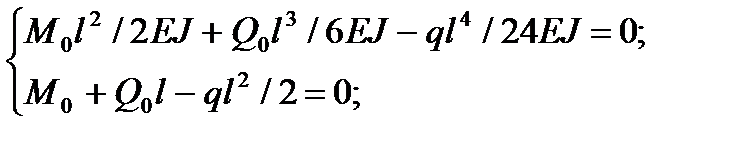
найдем:
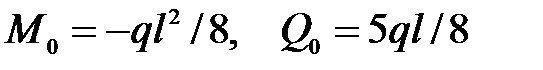 .
.
Теперь с помощью (б) можно построить эпюру М, а с учетом зависимости 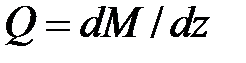 - эпюру поперечных сил. ·
- эпюру поперечных сил. ·
Отметим, что при определении начальных параметров данной статически неопределимой балки мы не обращались к уравнениям равновесия.
Расчет балок на жесткость
Расчет на жесткость производят, обычно, как проверочный расчет для обеспечения нормальных эксплуатационных свойств конструкции. Чтобы избежать появления чрезмерных перемещений, максимальный по модулю прогиб балки ограничивают допускаемым - [v], который, обычно, назначают в пределах от 1/200 до 1/600 длины пролета:
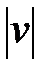 max£ [v], [v]
max£ [v], [v] 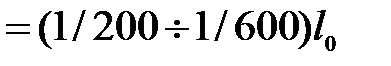 . (8.13)
. (8.13)
При расчете консольных балок длину 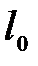 в формуле (8.13) полагают равной удвоенной длине консоли:
в формуле (8.13) полагают равной удвоенной длине консоли: 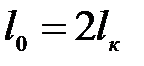 .
.
Напомним, что прогибы балки обратно пропорциональны ее жесткости:
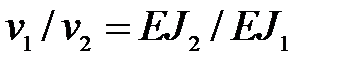 ,
,
поэтому если для балки с жесткостью 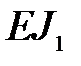 условие (8.13) не выполняется, прогибы новой балки с жесткостью
условие (8.13) не выполняется, прогибы новой балки с жесткостью 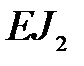 можно найти по формуле:
можно найти по формуле:
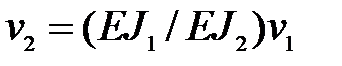 . (8.14)
. (8.14)
Пример 8.6.Проверить условие жесткости стальной и деревянной балок, рассмотренных в примере 7.1 (стр. 50), полагая EСТ = 200 ГПа, EДЕР = 10 ГПа, и принимая [v] 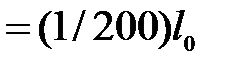 .
.
Решение.Нетрудно убедиться, что максимальный прогиб консольнойбалки, загруженной распределенной нагрузкой, будет равен  max=
max= 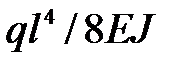 .
.
Для заданных консольных балок длиной 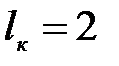 м допускаемый прогиб составит:
м допускаемый прогиб составит:
[v] 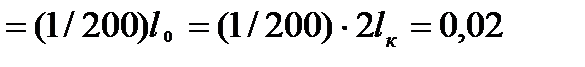 м.
м.
Максимальный прогиб стальной балки при 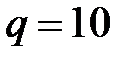 кН/м и
кН/м и 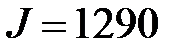 см4 равен:
см4 равен:
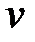 max=
max= 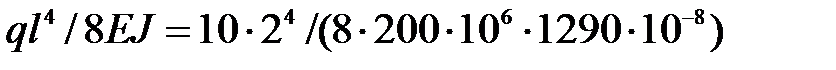 м = 0,008 м < [v].
м = 0,008 м < [v].
Отношение жесткостей стальной и деревянной балок равно 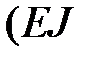 ст/
ст/ 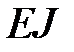 дер)
дер) 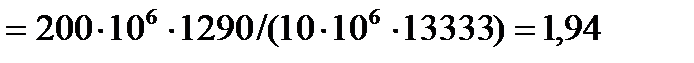 ; поэтому в силу (8.14):
; поэтому в силу (8.14):
vдер = 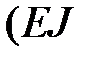 ст/
ст/ 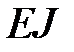 дер)
дер) 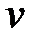 ст
ст 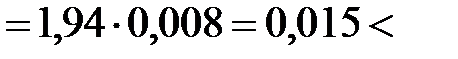 [v],
[v],
т.е. условие жесткости (8.13) также выполнено. ·
