F нүктесінің жылдамдығын, үдеуін, жанама және нормаль құраушы үдеулерін, қисықтық радиусын анықтау.

3.1. F нүктесінің жылдамдығын анықтау.F нүктесінің жылдамдығын координаттар өстеріне проекциялары арқылы анықтаймыз:

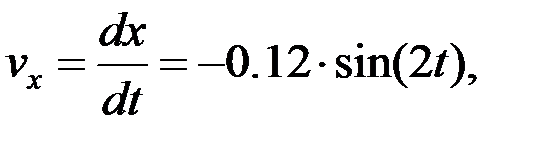
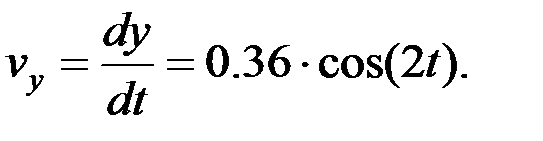
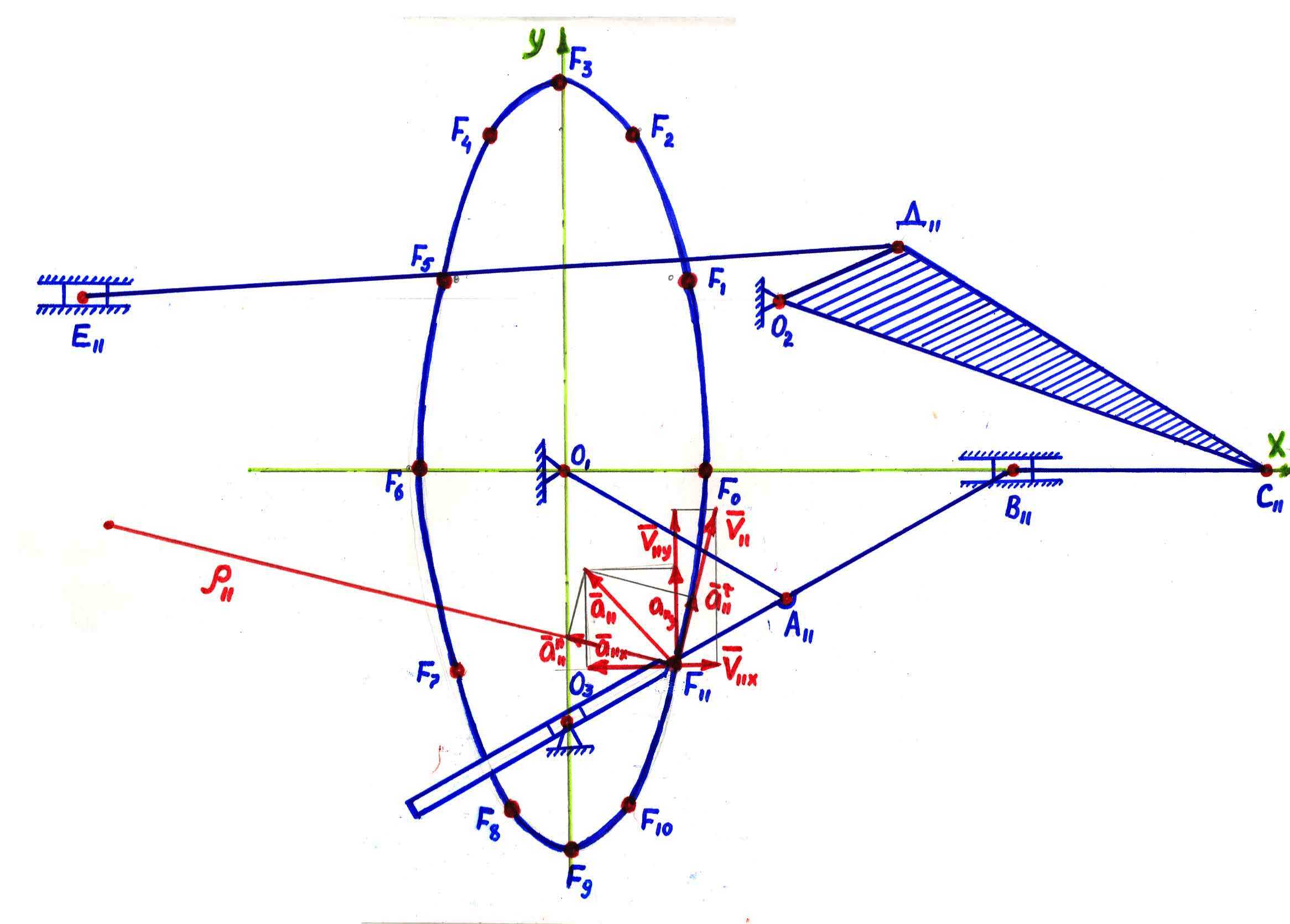
2.37-сурет

Егер 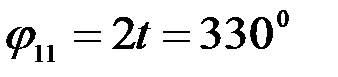-қа тең болса, онда:

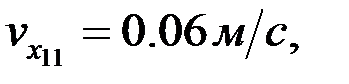
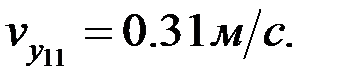
F нүктесінің жылдамдығының шамасы:

.

.

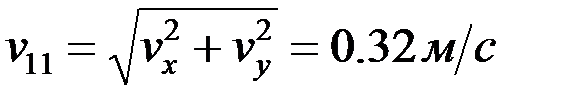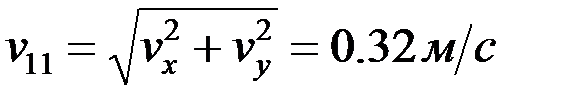3.2. F нүктесінің үдеуін анықтау. F нүктесінің үдеуін координаттар өстеріне проекциялары арқылы анықтаймыз:

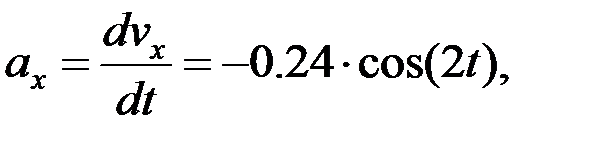
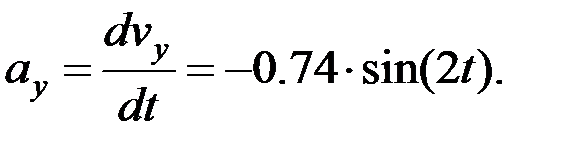
Егер 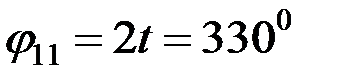-қа тең болса, онда:

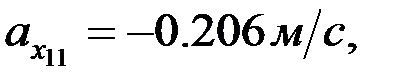
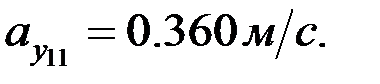
F нүктесінің үдеуінің шамасы:

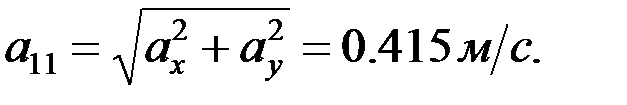
3.3. F нүктесінің жанама құраушы үдеуін анықтау.F нүктесінің жанама құраушы үдеуі мынадай өрнек арқылы анықталады:

.

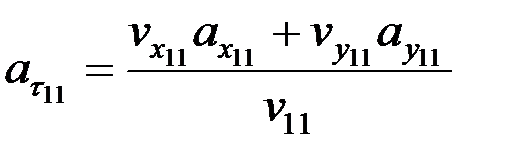Егер 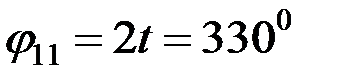-қа тең болса, онда:

3.4. F нүктесінің нормаль құраушы үдеуін анықтау.F нүктесінің нормаль құраушы үдеуі мынадай өрнек арқылы анықталады:

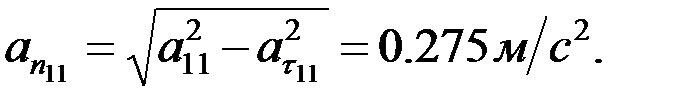
3.5. F нүктесінің қисықтық радиусын анықтау.F нүктесінің қисықтық радиусы мынадай өрнек арқылы анықталады:

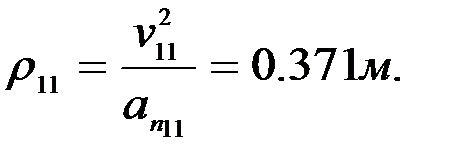
Механизм нүктелерінің жылдамдықтарын және буындарының бұрыштық жылдамдықтарын жылдамдықтар лездік центрі тәсілімен анықтау.

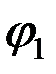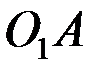4.1. Механизм нүктелерінің жылдамдықтарын анықтау. Механизмнің орнын берілген бұрышына сәйкес тұрғызамыз ( ) (2.34-сурет). буыны қозғалмайтын 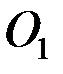центрін 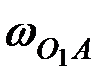бағытында айнала қозғалады, сондықтан:

,

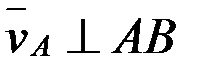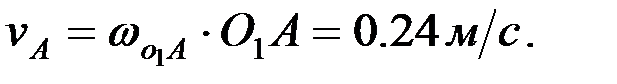
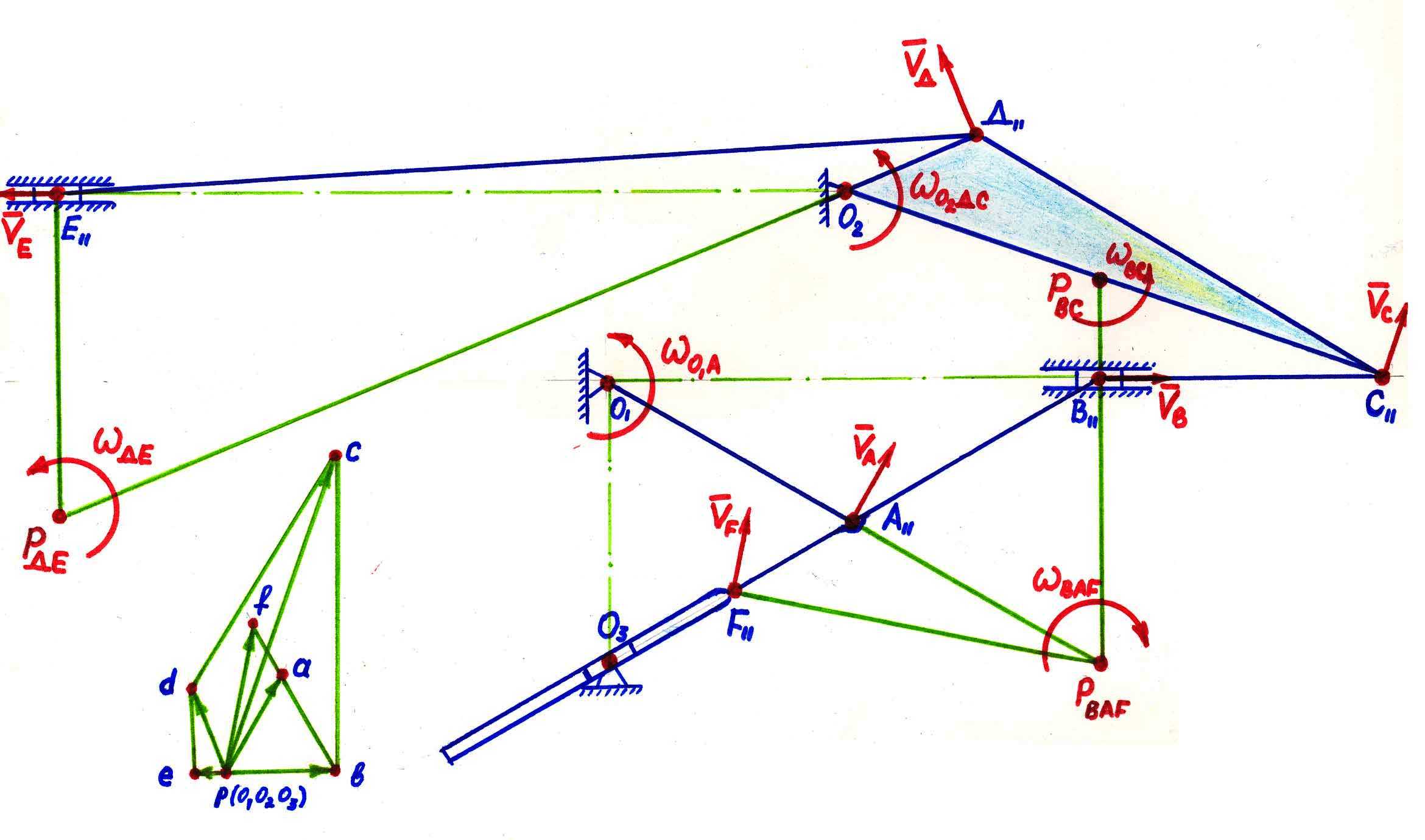
2.38-сурет

Механизм нүктелерінің жылдамдықтарын анықтау.

Жылжыма В-ның қозғалысы түзу сызықты болғандықтан, жылжыманың жылдамдық векторы, қозғалыс бағытымен бағыттас болады.

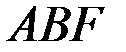буынының жылдамдықтар лездік центрі 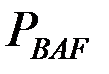, В және А нүктелері арқылы жүргізілген жылдамдық векторларына перпендикуляр түзулердің қиылысу нүктесі болады, ал F нүктесінің жылдамдық векторы 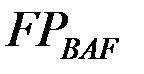кесіндісіне перпендикуляр бағытта бағыталады.

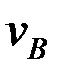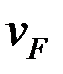және шамаларын мынадай қатынастар арқылы анықтаймыз:

,

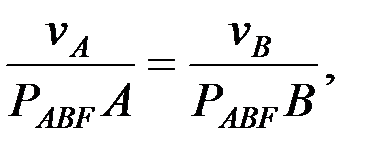
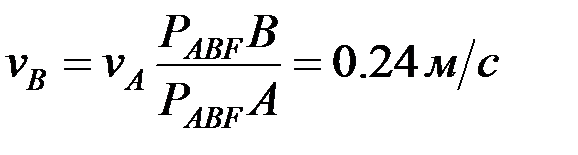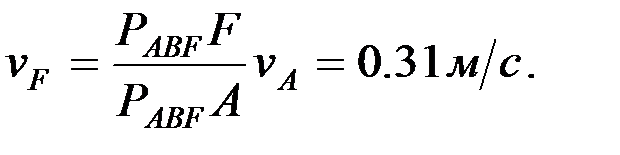
Жылдамдықтар лездік центрінен нүктелерге дейінгі ара қашықтық суретте өлшенеді.

Алдында орындалған амалдарға ұқсас амалдарды орындай отырып, ВС, 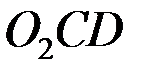, 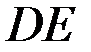буындарыныңсәйкес 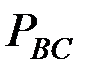, , 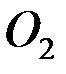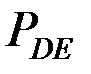жылдамдықтар лездік центрлерінің орындарын анықтаймыз және 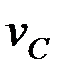, , 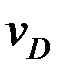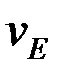шамаларын мынадай қатынастар арқылы анықтаймыз:

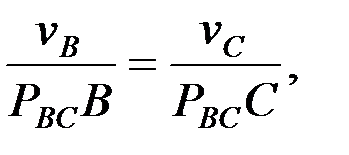
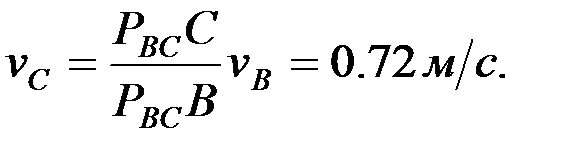
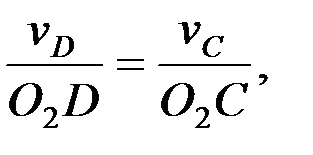
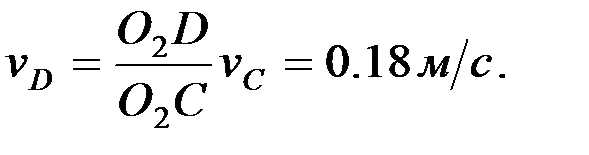
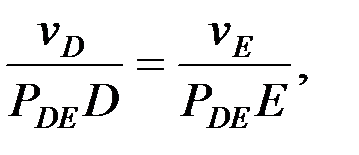
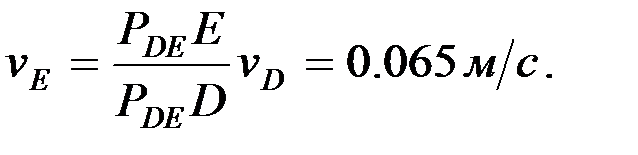
4.2. Буындарының бұрыштық жылдамдықтарын анықтау.Механизм буындарының бұрыштық жылдамдықтары мынадай өрнектер арқылы есептеледі, ал бағыттары нүктелер жылдамдықтарының бағыттарымен анықталады:

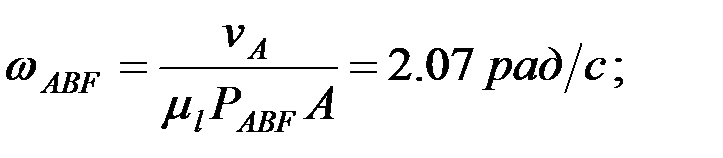
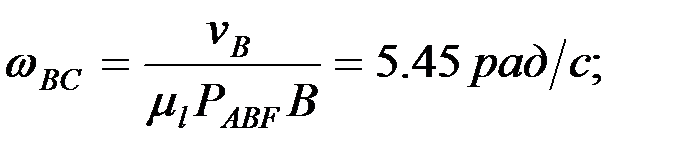
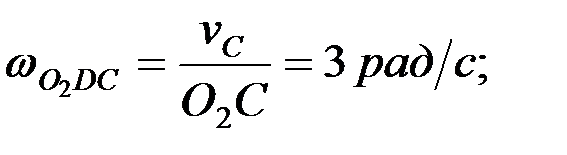
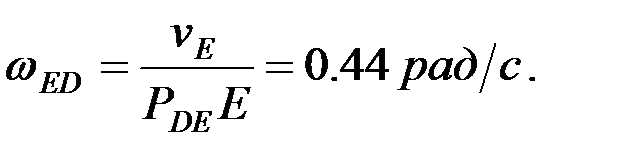
Механизм нүктелерінің жылдамдықтарын және буындарының бұрыштық жылдамдықтарын жылдамдықтар жобасын тұрғызу тәсілімен анықтау.

5.1. Механизм нүктелерінің жылдамдықтарын анықтау.Бастапқы буын үшін А нүктесінің жылдамдығы 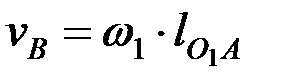формуласы бойынша аналиткалық түрде анықталады. Механизмнің қалған нүктелері 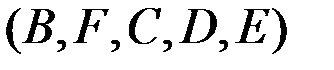үшін жылдамдықтар, векторлық теңдеулерді графикалық жолмен шешу арқылы және ұқсастық ережесі бойынша анықталады. В нүктесінің жылдамдығын мынадай векторлық теңдеулерді графикалық жолмен шешу арқылы анықтайды:

,

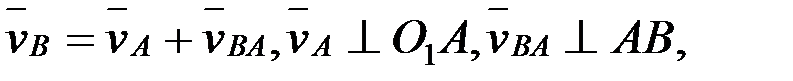
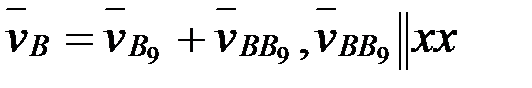мұндағы вектор 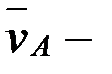шамасы және бағыты жөнінен белгілі ( 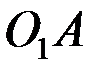түзуіне перпендикуляр және 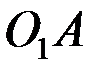буынының бұрыштық жылдамдығының бағытымен бағыттас);

вектор 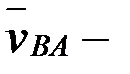В нүктесінің АВ буыны А нүктесіне қатысты айнала қозғалғандағы жылдамдығы, бағыты АВ түзуіне перпендикуляр, шамасы белгісіз;

вектор 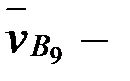тоғызыншы тірек нүктесінің жылдамдығы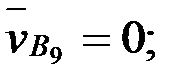

вектор 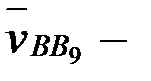В нүктесініңтірекке қатысты салыстырмалы жылдамдығы, бағыты 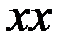түзуі бойымен сәйкес, шамасы белгісіз;

вектор 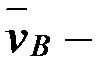В нүктесінің ізделініп отырған жылдамдығы, бағыты 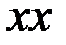түзуі бойымен бағыттас, шамасы белгісіз.

Жылдамдықтар жобасын төмендегі тәртіп бойынша тұрғызамыз:

бірінші теңдеуге сәйкес жобаның полюсінен (еркін алынған p нүктесі) бастап, 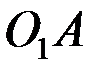түзуіне перпендикуляр, жобада А нүктесінің жылдамдығы үшін, ұзындығы 24 мм –тең, ра кесіндісін саламыз;

а нүктесінен АВ түзуіне перпендикуляр 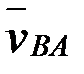жылдамдығының бағытын саламыз;

екінші векторлық теңдеуге сәйкес 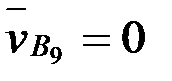болғандықтан, жобаның полюсінен 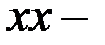ке параллель бағытта жылдамдығының бағытын саламыз. Сонымен, В нүктесінің жылдамдық соңы болатын b нүктесін табамыз. 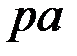және 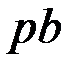кесінділері 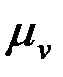масштабында 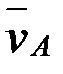және 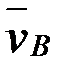жылдамдықтарын кескіндейді.

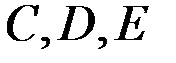нүктелерінің жылдамдықтарын мынадай векторлық теңдеулерді графикалық жолмен шешу арқылы анықтайды:

, ,

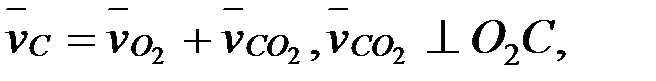
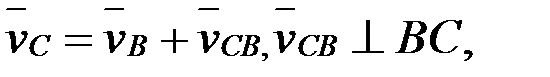
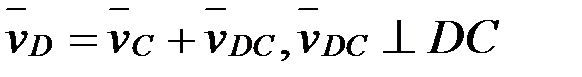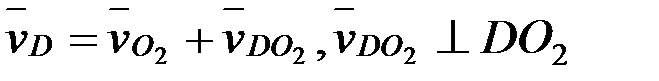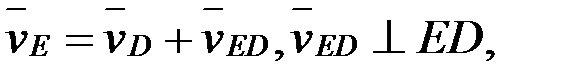
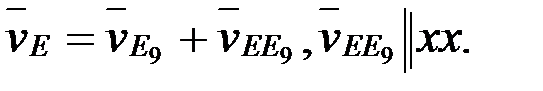
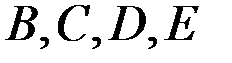нүктелерінің жылдамдықтарының шамаларын анықтау үшін жылдамдықтар жобасының масштабын анықтаймыз:

,

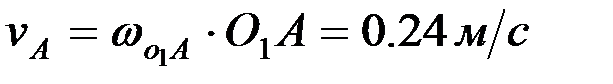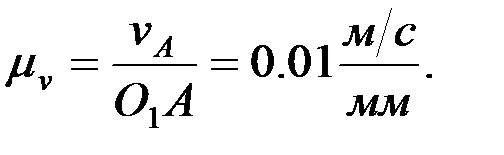
Сонда:

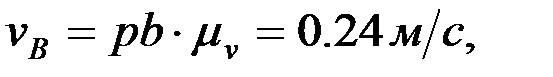
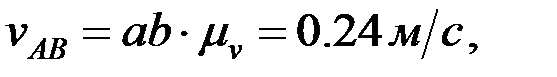
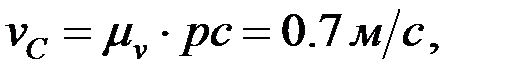
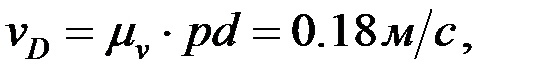
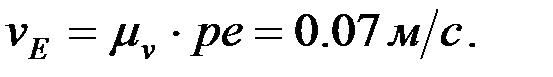
F нүктесінің жылдамдығын ұқсастық ережесі бойынша анықтайды:

5.2. Бұрыштық жылдамдықтарын анықтау. Механизм буындарының бұрыштық жылдамдықтары мынадай өрнектер арқылы есептеледі:

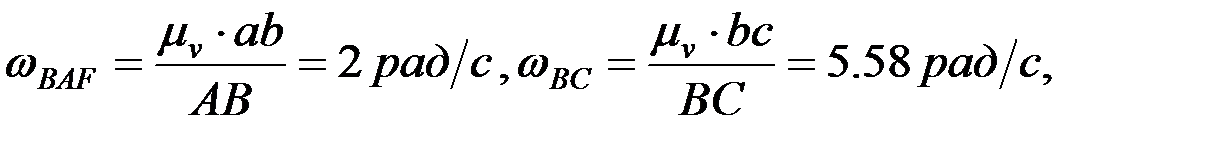
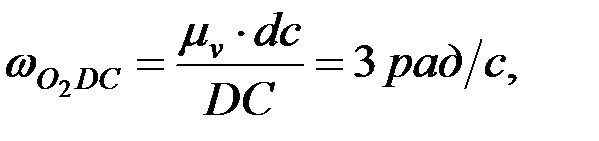
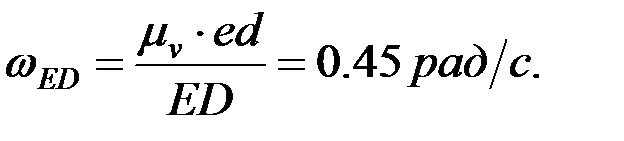
Механизм нүктелерінің үдеулерін және буындарының бұрыштық үдеулерін үдеулерді қосу теоремасын (проекциялық әдіс) пайдаланып анықтау.

6.1. Механизм нүктелерінің үдеулерін анықтау.В нүктесінің толық үдеуін, мына формуланы қолдану арқылы табамыз:

,

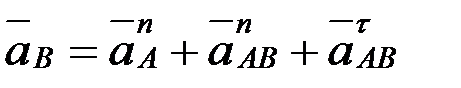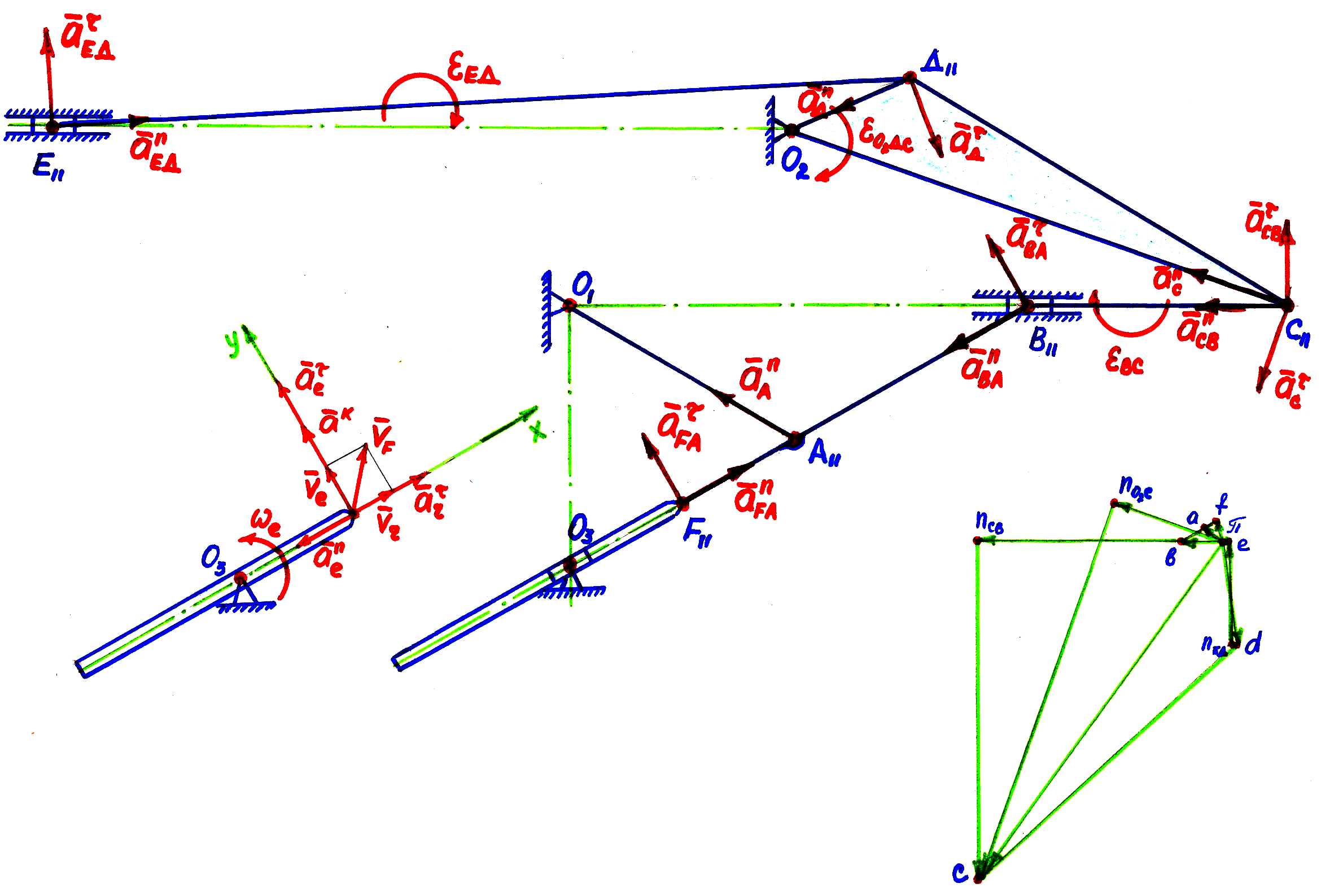
2.39-сурет

мұндағывектор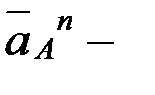полюс ретінде қабылданған нүктенің үдеуі, шамасы 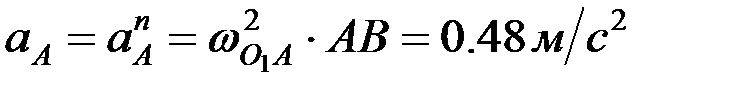, О₁ айналу центріне қарай бағытталады; вектор 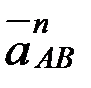- өске ұмтылғыш үдеу, модулі 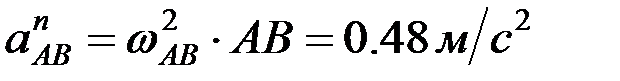, АВ бойымен полюске қарай бағытталады; вектор 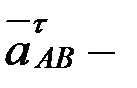айналдырушы үдеу, шамасы белгісіз, АВ-ға перпендикуляр айналыс болатын жаққа қарай бағытталады.

В нүктесінің толық үдеуі ны және 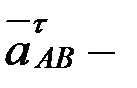айналдырушы үдеуді табу үшін векторлық теңдіктің екі жағында координаттар өстеріне проекциялаймыз:

,

.

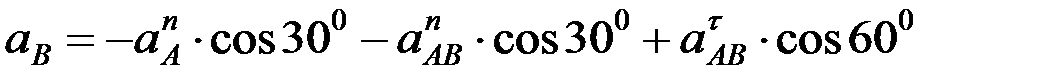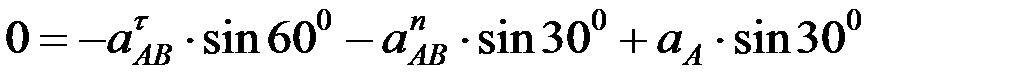Осы соңғы теңдіктердің көмегімен, іздеп отырған үдеулерді табамыз:

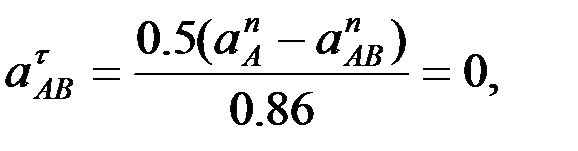
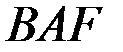буынының бұрыштық үдеуі: .

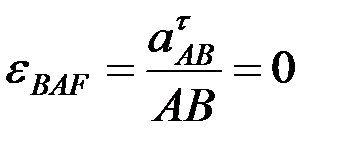F нүктесінің толық үдеуін, мына формуланы қолдану арқылы табамыз:

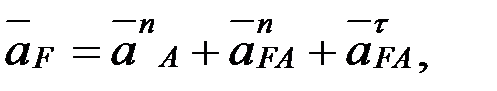
мұндағывектор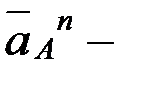полюс ретінде қабылданған нүктенің үдеуі, шамасы 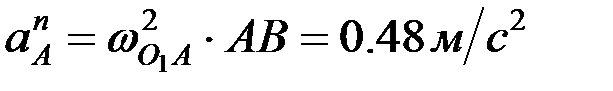, О₁ айналу центріне қарай бағытталады. вектор 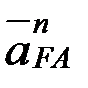- өске ұмтылғыш үдеу, модулі 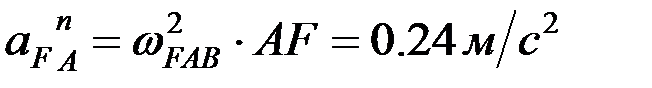, АВ бойымен полюске қарай бағытталады. Үшінші вектор 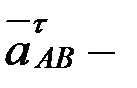айналдырушы үдеу, модулі

.

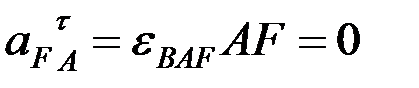Алдыңғы векторлық теңдіктің екі жағында 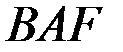бойымен бағытталған өске және оған перпендикуляр өске проекциялаймыз:

.

Осыдан:

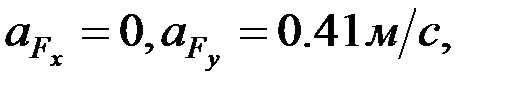
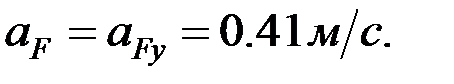
С нүктесінің толық үдеуін, мына формулаларды қолдану арқылы табамыз:

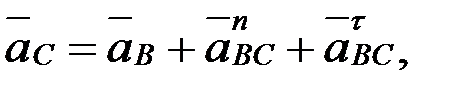
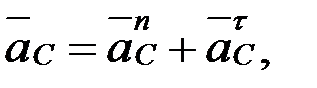
мұндағывектор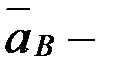полюс ретінде қабылданған нүктенің үдеуі, шамасы 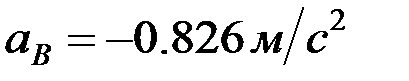; вектор 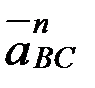- өске ұмтылғыш үдеу, шамасы 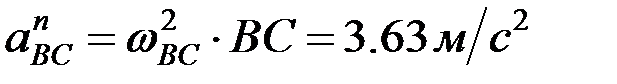, ВС бойымен полюске қарай бағытталады; вектор 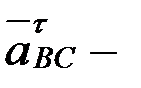айналдырушы үдеу, шамасы 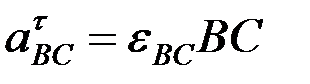белгісіз; вектор 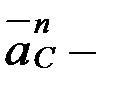өске ұмтылғыш үдеу, шамасы 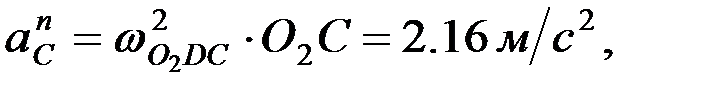О₂ айналу центріне қарай бағытталады; вектор 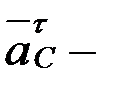айналдырушы үдеу, шамасы белгісіз, 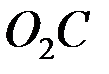-ға перпендикуляр айналыс болатын жаққа қарай бағытталады.

Алдыңғы векторлық теңдіктің екі жағында координаттар өстеріне проекциялаймыз:

.

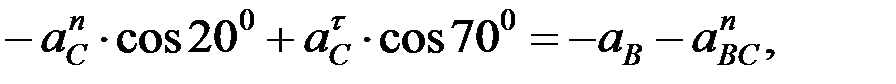
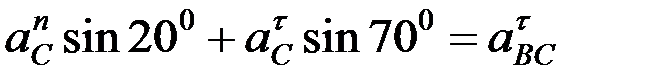Осыдан:

, .

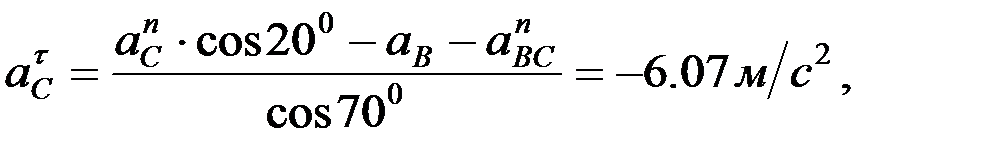
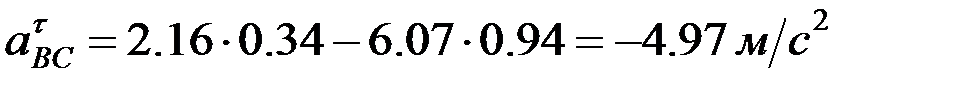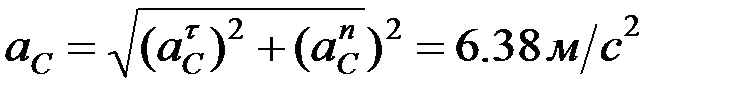ВС және О₂СD буындарының бұрыштық үдеулері мынадай өрнектер арқылы есептеледі:

, .

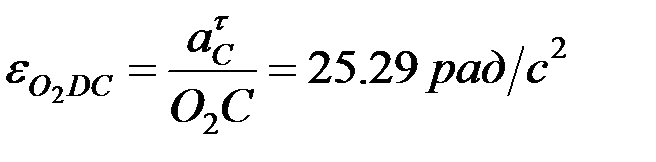D нүктесінің толық үдеуін, мына формуланы қолдану арқылы табамыз:

,

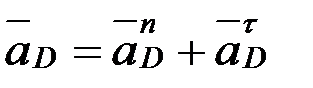мұндағы вектор 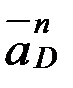- өске ұмтылғыш үдеу, шамасы 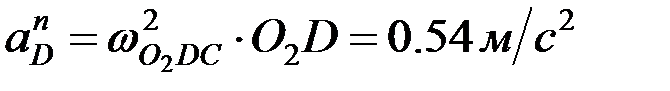, 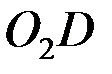бойымен айналу центріне қарай бағытталады, ал вектор 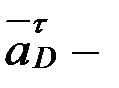айналдырушы үдеу, шамасы 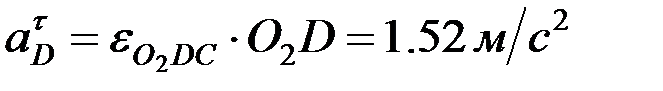. D нүктесінің толық үдеу шамасы:

.

Е нүктесінің толық үдеуін, мына формуланы қолдану арқылы табамыз:

,

мұндағывекторлар 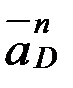. 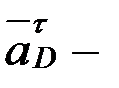шамалары және бағыттары жөнінен белгілі; вектор 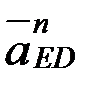- өске ұмтылғыш үдеу, шамасы 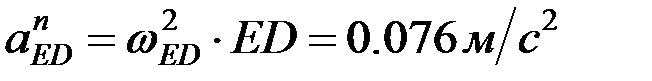, ED бойымен полюске қарай бағытталады; вектор 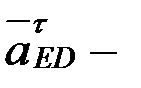айналдырушы үдеу, шамасы 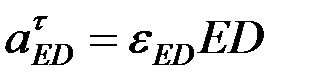белгісіз, 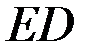-ға перпендикуляр айналыс болатын жаққа қарай бағытталады. Алдыңғы векторлық теңдіктің екі жағында координаттар өстеріне проекциялаймыз:

.

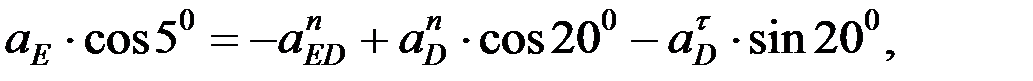
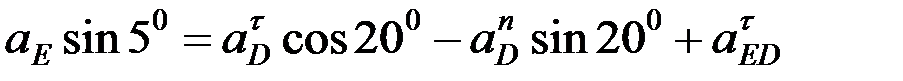Осыдан:

,

.

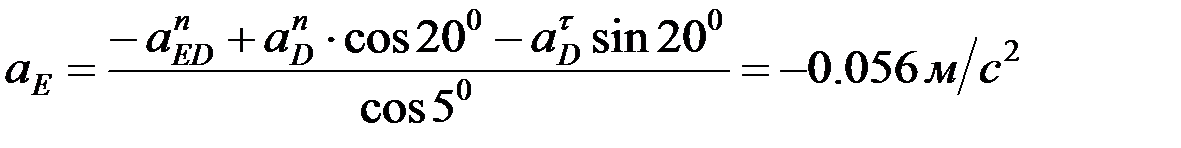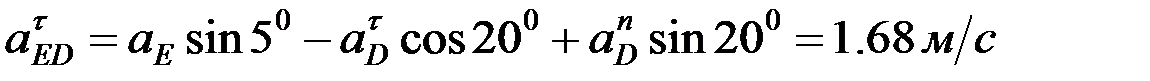6.2. Буындарының бұрыштық үдеулерін анықтау.Механизм буындарының бұрыштық үдеулері мынадай өрнектер арқылы есептеледі:

, ,

, .

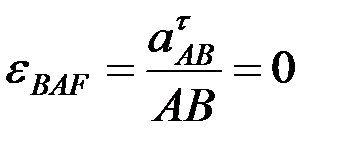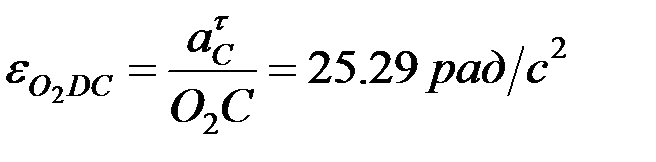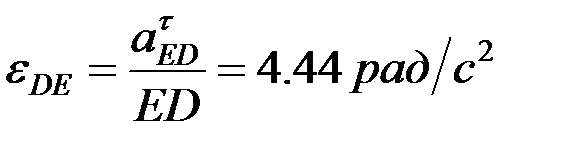Механизм нүктелерінің үдеулерін және буындарының бұрыштық үдеулерін үдеулер жобасын тұрғызу тәсілімен анықтау.

7.1. Механизм нүктелерінің үдеулерін анықтау. Үдеулер жобасын 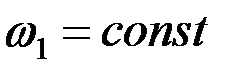болатынын ескере отырып тұрғызамыз. Бастапқы буын үшін А нүктесінің үдеуі 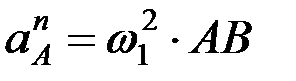формуласы бойынша аналитикалық түрде анықталады. Механизмнің қалған нүктелері 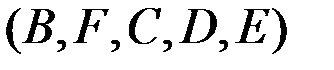үшін үдеулері, векторлық теңдеулерді графикалық жолмен шешу арқылы және ұқсастық ережесі бойынша анықталады. В нүктесінің үдеуін мынадай векторлық теңдеулерді графикалық жолмен шешу арқылы анықтайды:

, ,

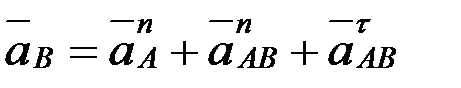мұндағывектор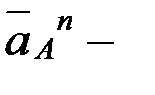полюс ретінде қабылданған нүктенің үдеуі, шамасы 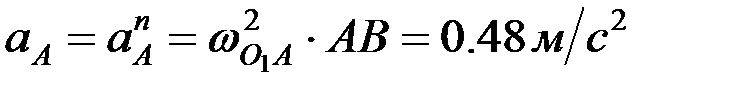, О₁А-ға параллель; вектор 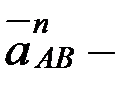өске ұмтылғыш үдеу, шамасы 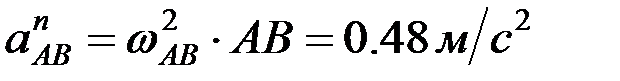, АВ-ға параллель; вектор 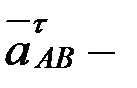айналдырушы үдеу, шамасы белгісіз, АВ-ға перпендикуляр; вектор 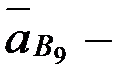тіректе жататын нүктесінің үдеуі, шамасы 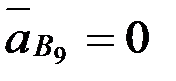; вектор 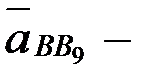В нүктесінің тіреке қатысты салыстырмалы үдеуі, шамасы белгісіз, xx-ке параллель.

Үдеулер жобасын мынадай тәртіп бойынша тұрғызамыз:

бірінші векторлық теңдеуге сәйкес жобаның полюсінен (еркін алынған 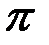нүктесі) бастап, 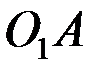түзуіне параллель, жобада А нүктесінің үдеуі үшін, ұзындығы 6мм–ге тең, 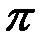а кесіндісін саламыз;

а нүктесінен АВ түзуіне параллель 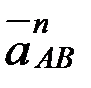үдеуін кескіндейтін ұзындығы мынадай теңдікпен анықталатын 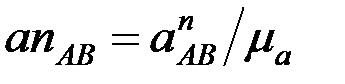кесіндісін саламыз;

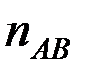нүктесінен АВ түзуіне перпендикуляр түзу саламыз;

екінші векторлық теңдеуге сәйкес жобаның полюсінен бастап хх түзуіне параллель түзу саламыз. Осы түзу 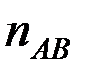нүктесінен АВ түзуіне перпендикуляр түзумен 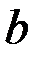нүктесінде қиылысады. 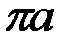, , 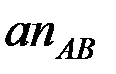, , 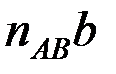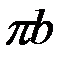кесінділері 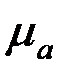масштабында 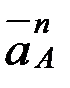, , 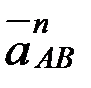, 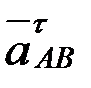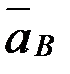үдеулерін кескіндейді.

нүктелерінің үдеулерін мынадай векторлық теңдеулерді графикалық жолмен шешу арқылы анықтайды:

.

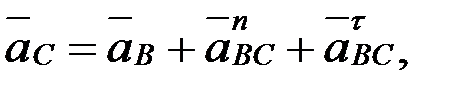
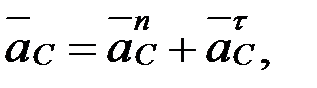
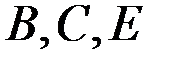нүктелерінің үдеулерінің шамаларын анықтау үшін, үдеулер жобасының масштабын анықтаймыз:

, .

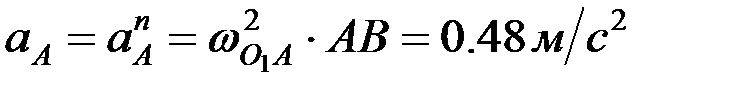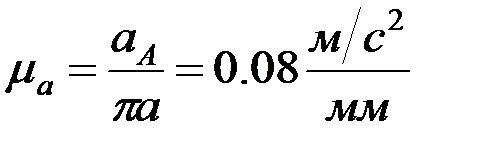Сонда:

, , .

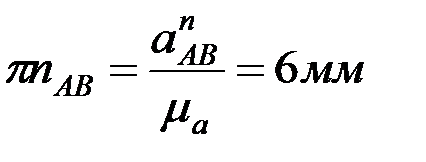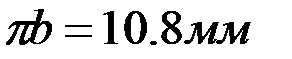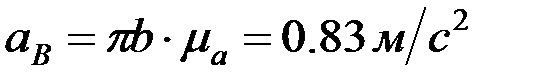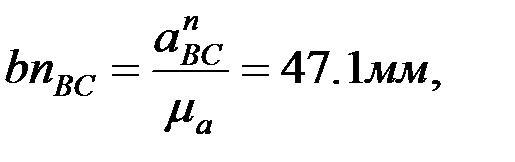
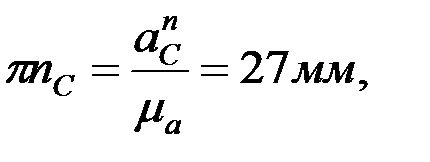
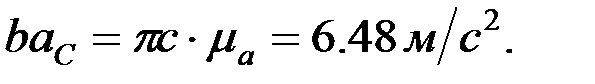
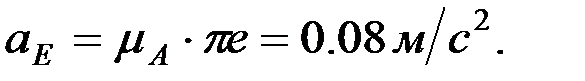
F және D нүктелерінің үдеулерін ұқсастық ережесі бойынша анықтайды:

,

,

, .

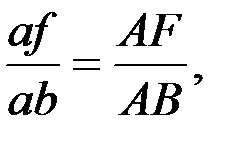
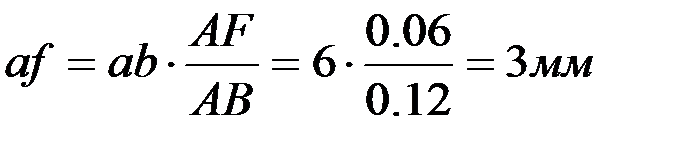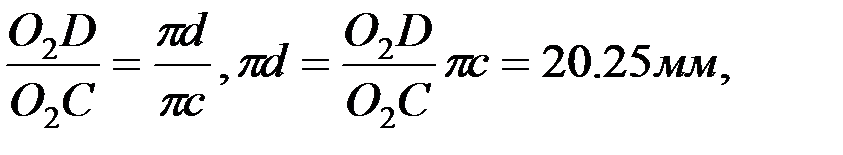
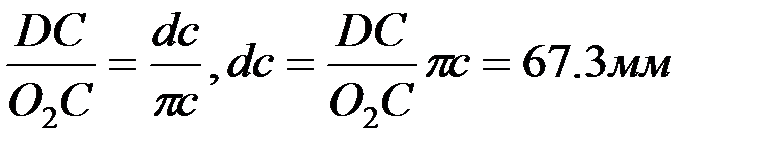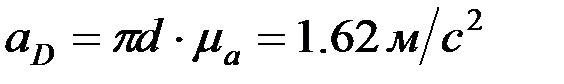7.2. Бұрыштық үдеулерін анықтау. Механизм буындарының бұрыштық үдеулері мынадай өрнектер арқылы есептеледі:

,

, .

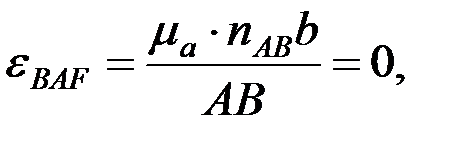
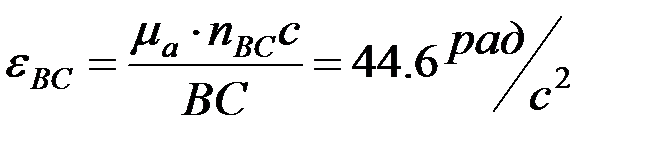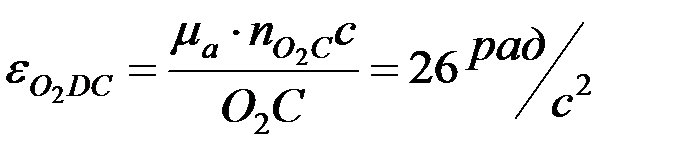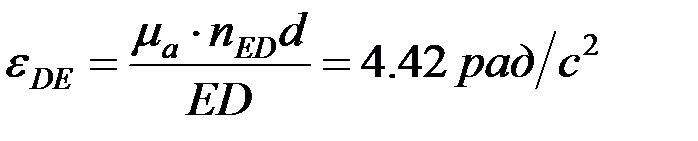8. Кулисалы механизм F нүктесінің абсолют жылдамдығының жіне үдеуінің құраушыларын анықтау.

9. Кулисалы механизм буынының бұрыштық жылдамдығын, бұрыштық үдеуін электронды есептеу машинасының көмегімен анықтау.Кулисаның 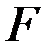нүктесінің абсолют жылдамдығы белгілі:

.

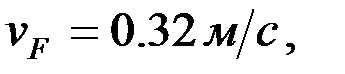
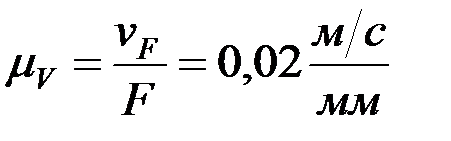Жылдамдықтарды қосу теоремасы бойынша:

.

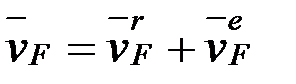Салыстырмалы жылдамдығы 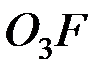түзуі бойымен, ал тасымал жылдамдығы осы түзуге перпендикуляр бағытталған. Диагоналі 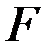нүктесінің жылдамдығы 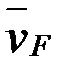, ал қабырғалары 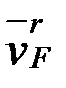, 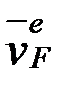болатын параллелограм тұрғызамыз.

Суретте өлшеу арқылы алатынымыз:

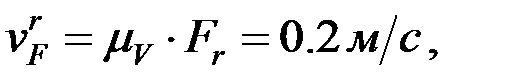
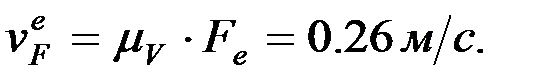
Кулисаның тасымал бұрыштық жылдамдығы мынадай өрнек арқылы анықталады:

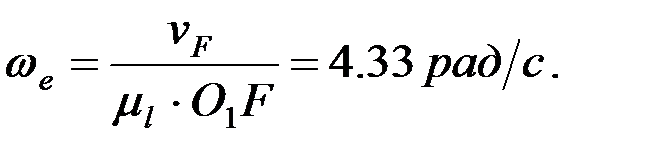
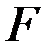нүктесінің абсолют үдеуі салыстырмалы, тасымал және кориолис үдеулерінің геометриялық қосындысына тең:

,

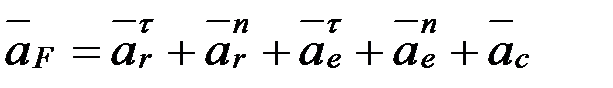мұндағы вектор 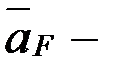абсолют үдеу, шамасы 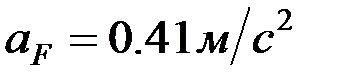; вектор 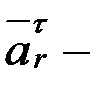салыстырмалы жанама құраушы үдеу, шамасы белгісіз; вектор 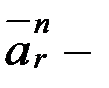салыстырмалы нормаль құраушы үдеу, шамасы ;

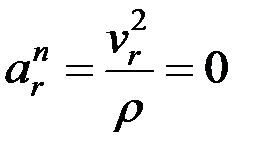вектор 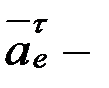тасымал жанама құраушы үдеу, шамасы белгісіз; вектор 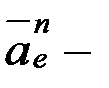тасымал нормаль құраушы үдеу, шамасы 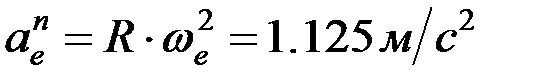; вектор 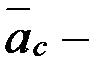кориолис үдеуі, шамасы .

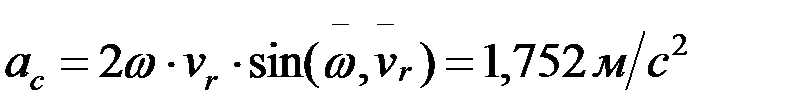Алдыңғы векторлық теңдіктің екі жағында координаттар өстеріне проекциялаймыз:

.

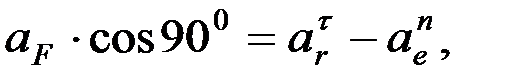
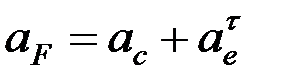Осыдан:

,

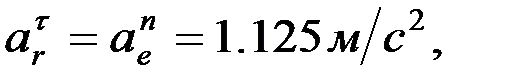
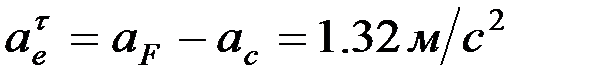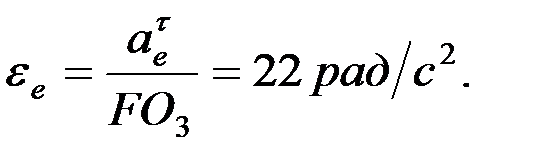
9. Кулисалы механизм буынының бұрыштық жылдамдығын, бұрыштық үдеуін электронды есептеу машинасының көмегімен анықтау.Кулисалы механизмнің кез келген орны үшін мынадай векторлық теңдіктерді құрамыз:

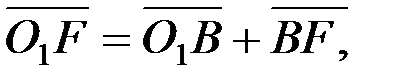
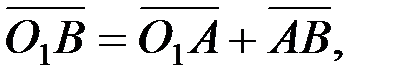
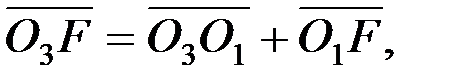
немесе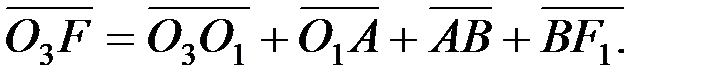

Теңдіктердің екі жағында координаттар өстеріне проекциялаймыз:

.

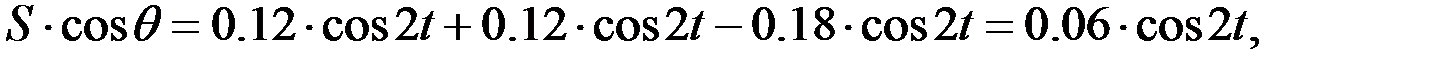
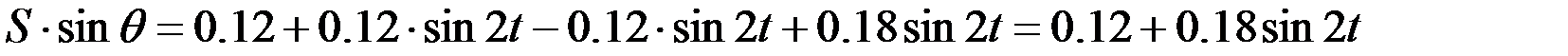Уақыт бойынша екі рет дифференциалдаймыз. Бір рет дифференциалдасақ бұрыштық жылдамдық 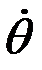және салыстырмалы жылдамдық 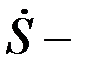ге қатысты алгебралық теңдеулерді аламыз:

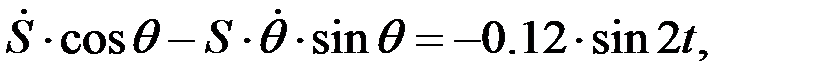
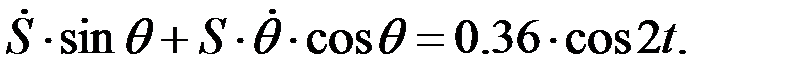
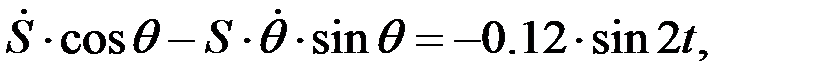
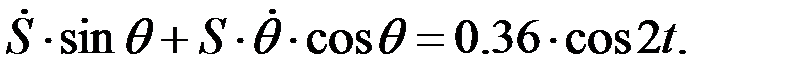
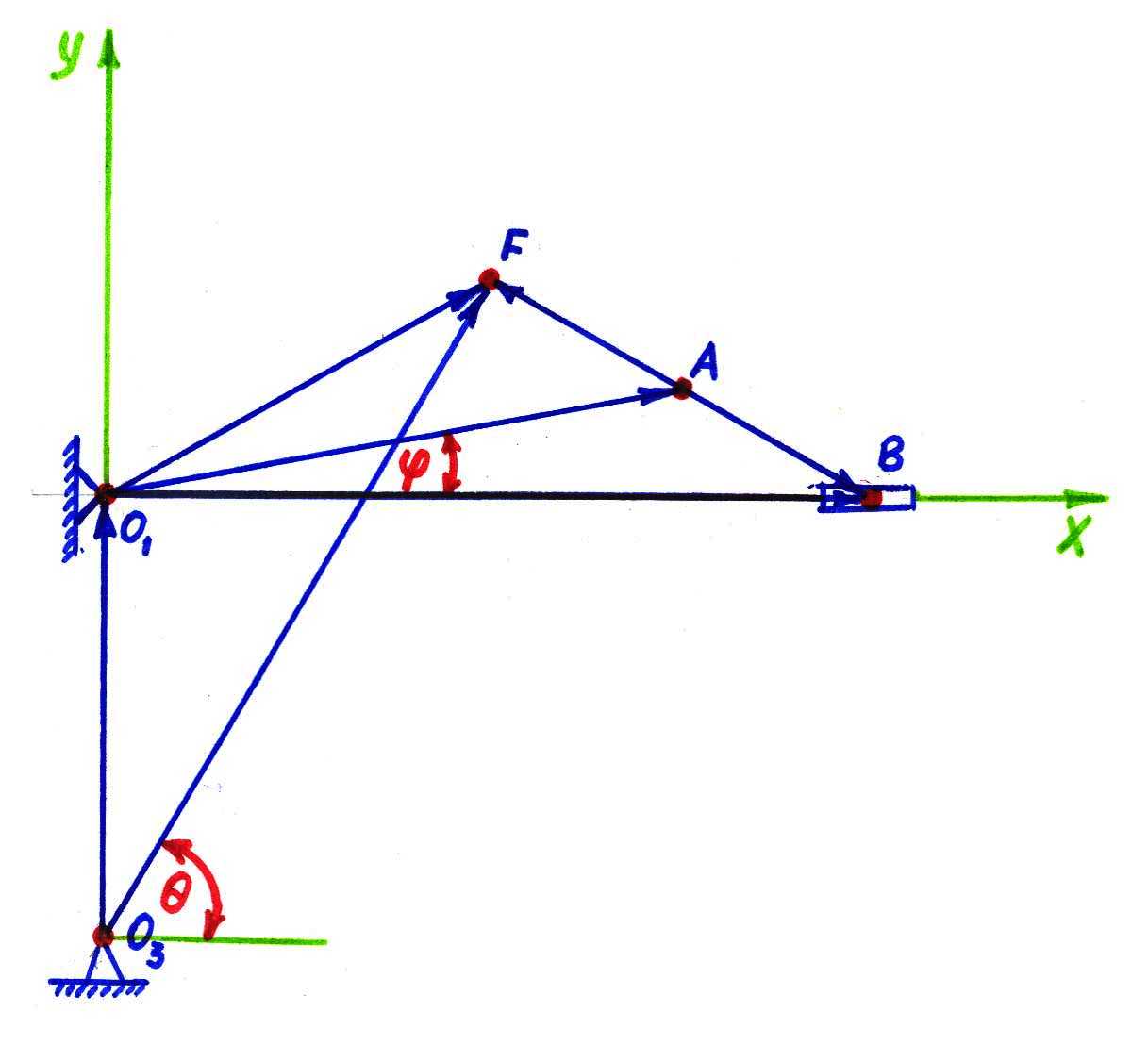
2.40-сурет

Екінші рет дифференциалдасақ бұрыштық үдеу 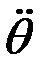және салыстырмалы үдеу 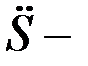ге қатысты алгебралық теңдеулерді аламыз:

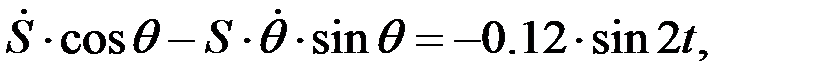
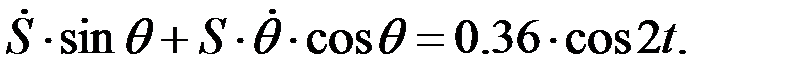
Екінші рет дифференциалдасақ, бұрыштық үдеу 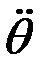және салыстырмалы үдеу 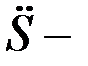ге қатысты алгебралық теңдеулерді аламыз:

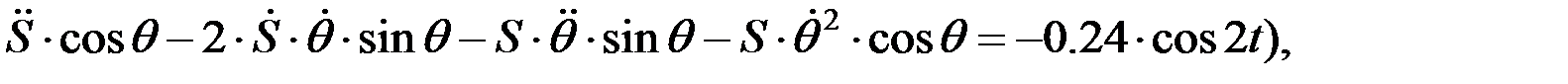
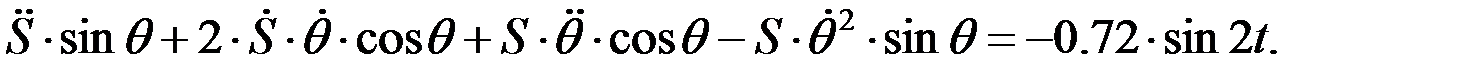
Екі теңдеулер жүйесін 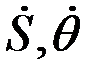және 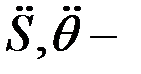ге қатысты шешеміз:

( )

,

( )

.

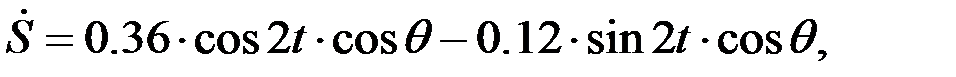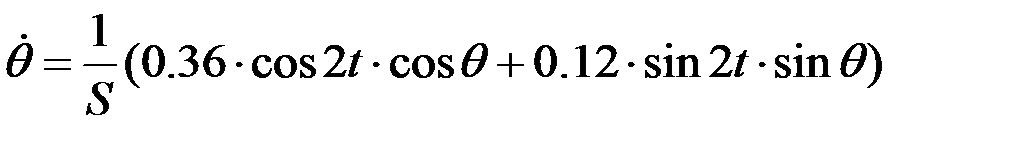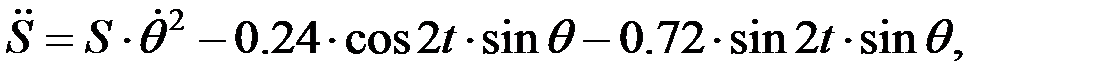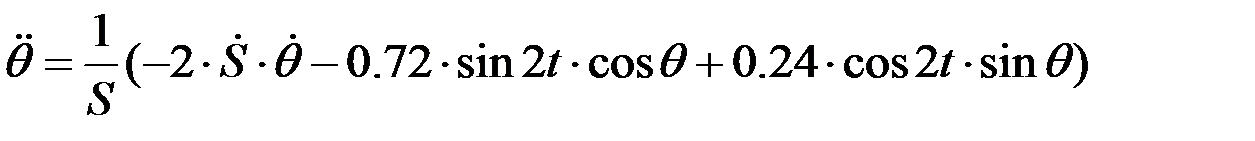Программаны жазу

ЭЕМ көмегімен және 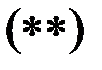теңдеулер жүйесін шешеміз. Қадамы басылым қадамына тең Эйлер әдісін пайдаланамыз. 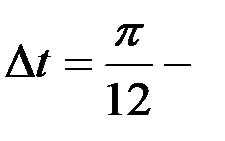уақытқа байланысты қадам, 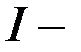интеграция номері, мынадай шекті аралықта өзгереді .

,

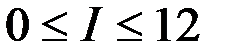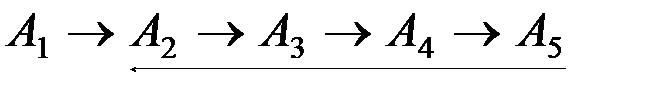
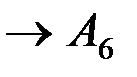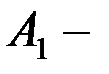берілгенін енгізу;

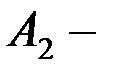( ) теңдеулерінің шешімі, 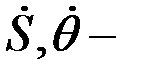ні анықтау;

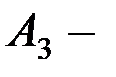( ) теңдеулерінің шешімі, 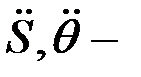ні анықтау;

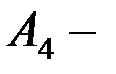қорытындыларды печатқа беру;

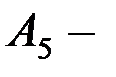егер 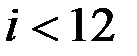болса, онда есептеуді қайталау;

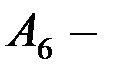жұмыстың соңы.

2.3-кесте

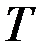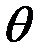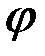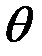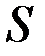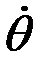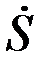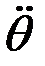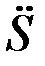	0.0	0.0	1.1071	0.1342	1.2000	-4.1600	0.3220	0.0859
	0.2616	0.5236	1.3282	0.2163	0.6154	-1.1069	0.2882	-0.3175
	0.5236	1.0472	1.4525	0.2775	0.4424	-0.3477	0.1677	-0.5785
	0.7854	1.5708	1.5708	0.3000	0.4000	0.0000	0.0000	-0.6720
	1.0472	2.0944	1.6791	0.2775	0.4424	0.3478	-0.1677	-0.5785
	1.3090	2.6180	1.8134	0.2163	0.6154	1.1969	-0.2882	-0.3175
	1.5708	3.1416	2.0345	0.1342	1.2000	4.1602	-0.3220	0.0859
	1.8326	3.6652	2.6180	0.0606	4.0001	20.7848	-0.2078	0.9500
	2.0944	4.1888	4.0161	0.0468	4.1729	-19.3298	0.00714	0.2591
	2.3562	4.7124	4.7124	0.0600	2.0000	0.0002	0.0000	-0.4800
	2.6180	5.2360	-0.8745	0.0468	4.1731	10.3304	-0.0714	0.2592
	2.8798	5.7596	0.5236	0.0600	3.9999	-20.7841	0.2079	0.9600
	3.1416	6.2832	1.1071	0.1342	1.2000	-4.1595	0.3220	0.0859

Динамика