Математикалық индукция әдісінің геометриялық есептерді шығаруда қолданылуы

Жазықтықта кез келген екеуі өзара параллель болмайтын және кез келген үшеуі бір нүктеден өтпейтін п түзу жүргізілген. Бұл түзулер жазықтықты неше бөлікке бөлетіндігін анықтаңдар.

Шешуі: Жазықтықты бір түзу 2 бөлікке, 2 түзу 4 бөлікке, 3түзу 7 облысқа, 4 түзу 11 облысқа бөлетіндігін байқау қиын емес.

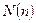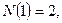
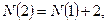
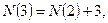
Айталық п түзу жазықтықты бөлікке бөлсін. Сонда 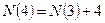тағы солсияқты 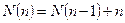болатындығы айқын.

Төмендегі п теңдікті өзара мүшелеп қосып, мынаны табамыз.

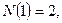
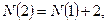
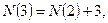
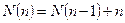
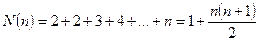(1)

Енді осы теңдіктің дұрыстығын математикалық индукция әдісімен дәлелдейік. 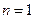үшін теңдіктің дұрыстығы айқын.

Айталық жазықтықта жүргізілген п түзу оны 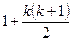бөлікке бөлгенде, жазықтықтағы 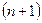түзу 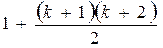бөлікке бөлетінін дәлелдейміз.

Шынында да

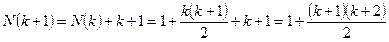
болатындықтан, жазықтықтағы жүргізілген п түзу оны 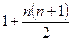бөлікке бөлетіндігі дәлелденді.

Жауабы:жазықтықты 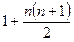-ге бөледі.

7. Дедукция

Дедукция теориялық мәселелер формальды сипатталатын, білімдер облысында (мысалы, математикада) үлкен рөл атқарады. Қазіргі заман ғылымында формализациялау кең түрде қолданыла бастауына байланысты дедукцияның тану үрдісіндегі маңызы арта түсуде.

Математикадағы дедуктивтік әдіс деп кейбір теориялық жүйелердің қатаң логикалық салдары болатын нақтылы деректер алу немесе ақиқат қорытынды шығару деп түсініледі.

Логикада дедуктивтік әдістің мынадай түрлері бөліп көрсетіледі: аксиоматикалық, генетикалық (конструктивтік) және генетикалық-дедуктивтік.

Аксиоматикалық әдіс бойынша ғылыми теорияны құрудың жолы мынадай: берілген теорияның негізі ретінде қандай да бір дәлелдеусіз жағдайлар (оған енетін анықтама берілмейтін ұғымдар) және постулаттар алынады, ал басқа барлық білімдер логикалық ережелер және заңдар бойынша қорытылып шығарылады.

Генетикалық әдіс аксиоматикалық әдісті негіздеудің қажеттігі нәтижесінде пайда болып және ол Д.Гильберттің еңбектерінде дамытылды.

Егер аксиоматикалық әдісте бастапқы үшін элементтеріне логикалық амалдар қолдануға болатын пікірлер жүйелі алынса, генетикалық әдісте бастапқы үшін берілген объектілердің бар болуы және ол объектілерге қолданылатын іс әрекеттер жүйесі алынады.

Қазіргі кезде генетикалық әдіс математиканы негіздеу үшін кең түрде қолданылуда.

Генетика-дедуктивтік әдістің мәні мынада: болжам ретінде жалпы жағдайлар алынады және одан шығатын жеке салдарлар эмпирикалық бақылаулармен салыстырылады. Бұл әдіс жалпы жағдайларды жеке деректермен растайтын және негіздейтін логикалық ережелер мен белгілерді де қамтиды.

Басқа тану әдістерінен дедукцияның ерекшелігі – берілген бастапқы білімдер ақиқат болғанда, оның дұрыс қорытынды білімдер беретіндігінде. Дедуктивтік зерттеу жүргізу барысындағы жалпы принциптер және заңдар ғылымдардың жаңылыс жолға түсіп кетпеуіне, шындық дүниенің құбылыстарын дұрыс түсінуге мүмкіндік береді.

Біз жоғарыда жалпы ой қорытындысына сүйеніп, жасалынған жеке ой қорытындысын дедукция деп атадық.

Енді дедукцияға нақтылы мысалдар келтірейік.

1-мысал. 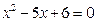тендеуінің дискриминантын есептеп, оның түбірлерінің болатындығын көрсетіңдер. Бізге квадрат теңдеулерді шешу туралы ережеге сәйкес оның дискриминанты оң таңбалы болса, оның әр түрлі екі нақты түбірлері болатындығын белгілі. Сонда 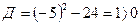болатындықтан 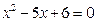теңдеуі де екі түбірге 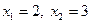ие болады.

2-мысал. 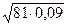өрнегінің мәнін табыңдар. Бұл өрнектің мәнін табу үшін мектептегі алгебра курсындағы жалпы жағдайды қамтитын мына теореманы пайдаланамыз.

Теорема. 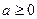және 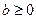болғанда 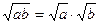болады. Соның үшін мынадай нәтиже аламыз:

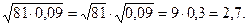
3-мысал. Мектептегі геометрия курсындағы косинустар теоремасының өрнегі мынадай:

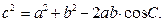(1)

Егер (1)-де 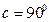болса, 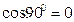, сондықтан 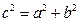(2) болады. Бізге (2) Пифагор теорема екені белгілі.

Сұрақтар:

1. Математиканы оқытудағы и ндукция.

2. Толымсыз индукция;

3. Толық индукция;

4. Математикалық индукция.

5. Математикалық индукция әдісінің теоремаларды дәлелдеуде

қолданылуы

Әдебиетер:

1. Ә.Бидосов. Орта мектепте математиканы оқыту методикасы. – Алматы: Мектеп, 1989. – 224 б.

2.Әбілқасымова А.Е., Көбесов А.К., Рахымбек Д., Кенеш Ә С. Математиканы оқыту теориясы мен әдістемесі. – Алматы: Білім,1998. – 208 б.

3. Бейсеков Ж., Рахымбек Д., Шарипов Т.А. Орта мектепте математиканы оқыту әдістемесіне арналған оқу құралы. – Шымкент,2003. - 179 б

Лекция