Корректные и некорректные задачи. понятие о методах регуляризации
Рассмотрим операторное уравнение вида
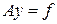 (4.16)
(4.16)
где 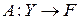 – некоторый оператор, действующий из метрического пространства
– некоторый оператор, действующий из метрического пространства 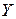 в метрическое пространство
в метрическое пространство 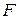 (обычно
(обычно 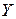 и
и 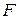 полные метрические пространства, в частности, банаховы).
полные метрические пространства, в частности, банаховы).
Определение 4.1.Задача нахождения элемента 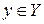 по заданному элементу
по заданному элементу 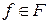 из уравнения (4.16) называется корректно поставленной по Адамару для тройки
из уравнения (4.16) называется корректно поставленной по Адамару для тройки 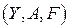 или просто корректной, если:
или просто корректной, если:
1) при каждом 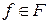 существует решение
существует решение 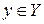 ;
;
2) это решение 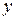 единственно в
единственно в 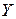 ;
;
3) решение непрерывно зависит от правой части уравнения (4.16)(т.е. из сходимости  по метрике пространства
по метрике пространства 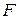 следует сходимость
следует сходимость 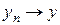 по метрике пространства
по метрике пространства 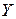 ).
).
При нарушении любого из этих трех условий задача (4.16) считается некорректной.
Первые два условия корректности, фигурирующие в определении 4.1, означают существование обратного оператора 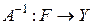 , третье условие – его непрерывность на всем пространстве
, третье условие – его непрерывность на всем пространстве 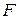 .
.
Часто требование непрерывной зависимости решения от правой части уравнения (4.16) заменяют условием его устойчивости:
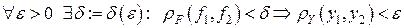 ,
,
где 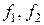 – произвольные элементы
– произвольные элементы 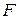 , а
, а 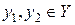 – отвечающие им решения (
– отвечающие им решения ( 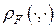 и
и 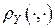 – метрики пространств
– метрики пространств 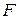 и
и 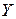 соответственно).
соответственно).
Несколько более широкая трактовка третьего условия корректности состоит в том, что в корректно поставленных задачах небольшие изменения в исходных данных (малые возмущения 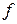 и
и  в (4.16)) вызывают небольшие изменения решения.
в (4.16)) вызывают небольшие изменения решения.
При нарушении второго условия корректности выход находят в том, что среди бесчисленного множества решений ищется решение, ближайшее к заданной точке 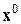 , называемой пробным решением. Такая точка может быть известна из каких-то априорных соображений (например, физического смысла задачи); в противном случае полагают
, называемой пробным решением. Такая точка может быть известна из каких-то априорных соображений (например, физического смысла задачи); в противном случае полагают 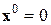 .
.
Определение 4.2. Решение уравнения (4.16), ближайшее к заданному пробному решению 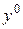 , называется нормальным относительно
, называется нормальным относительно 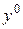 решением (или просто нормальным решением, если
решением (или просто нормальным решением, если 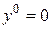 ).
).
Другими словами, нормальное относительно 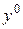 решение уравнения (4.16) – это проекция пробного решения
решение уравнения (4.16) – это проекция пробного решения 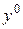 на множество решений этого уравнения. Если указанное множество выпукло, то как известно, такая проекция, а следовательно, и нормальное решение единственно.
на множество решений этого уравнения. Если указанное множество выпукло, то как известно, такая проекция, а следовательно, и нормальное решение единственно.
Для линейных алгебраических систем неустойчивость напрямую связана с их плохой обусловленностью.
В случае переопределенных, несовместных систем 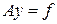 за решение принимается вектор
за решение принимается вектор 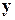 , минимизирующий функцию
, минимизирующий функцию
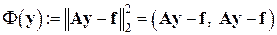
Эта функция всегда имеет неотрицательный минимум.
Определение 4.3.Вектор 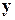 , на котором достигается
, на котором достигается 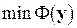 , называется псевдорешением системы
, называется псевдорешением системы 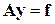 .
.
Из вида 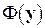 ясно, что если
ясно, что если 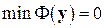 , то
, то 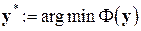 есть точное решение системы
есть точное решение системы 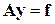 , т.е. псевдорешение обобщает понятия решение в привычном понимании.
, т.е. псевдорешение обобщает понятия решение в привычном понимании.
Для нахождения псевдорешение системы 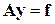 , вместо решения экстремальной задачи
, вместо решения экстремальной задачи 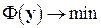 можно решать симметричную систему
можно решать симметричную систему
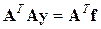 (4.17)
(4.17)
Действительно, так как
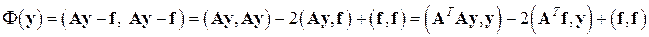 ,
,
Применяя необходимое (а в данном случае и достаточное) условие минимума и правила дифференцирования квадратичной и линейной форм, имеем
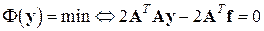
т.е. приходим к системе (4.17).
Введение понятия псевдорешения позволяет избавиться от несуществования, а понятие нормального решения – неединственности. Объединяя их, приходим к понятию нормального псевдорешения. При этом первое и второе требование корректности могут быть сняты.
Осознание того факта, что несуществование и неединственность решения уравнения (4.16) можно обойти путем обобщения (расширения) понятия решения и сужения множества, на котором ищется это обобщенное решение, привело к новой формулировке корректности.
Определение 4.4.Задача о нахождении решения 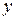 уравнения (4.16) с непрерывным оператором
уравнения (4.16) с непрерывным оператором  называется условно корректной или корректной по Тихонову, если:
называется условно корректной или корректной по Тихонову, если:
1) априори известно, что решение 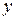 существует и принадлежит заданному множеству
существует и принадлежит заданному множеству 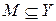 (множеству корректности, классу корректности);
(множеству корректности, классу корректности);
2) решение 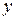 единственно в
единственно в 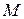 ;
;
3) бесконечно малым вариациям 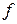 , не выводящим за пределы
, не выводящим за пределы 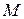 , соответствуют бесконечно малые вариации
, соответствуют бесконечно малые вариации 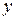 .
.
В основе общей стратегии построения устойчивых методов решения некорректных (неустойчивых) задач в операторной форме лежит понятие регуляризирующего оператора или, что то же, регуляризирующего алгоритма.
Определение 4.5.Пусть 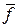 – фиксированное точное значение правой части уравнения (4.16), а
– фиксированное точное значение правой части уравнения (4.16), а 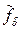 – его приближенное значение такое, что
– его приближенное значение такое, что 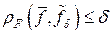 .
.
Оператор 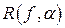 называется регуляризирующим оператором (регуляризирующим алгоритмом, регуляризирующим затором) для уравнения (4.16) в окрестности
называется регуляризирующим оператором (регуляризирующим алгоритмом, регуляризирующим затором) для уравнения (4.16) в окрестности 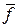 , если:
, если:
1) оператор 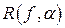 определен для любых
определен для любых  ,
, 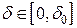 и
и 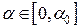 , где
, где 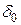 и
и 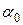 – некоторые предельные значения параметров
– некоторые предельные значения параметров 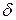 и
и 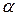 ;
;
2) существует такая зависимость  , что
, что 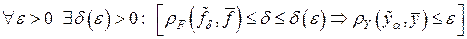 , где
, где 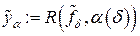 – регуляризованное решение уравнения (4.16), а элемент
– регуляризованное решение уравнения (4.16), а элемент 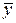 таков, что
таков, что 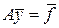 ; при этом должно быть
; при этом должно быть 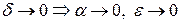 (т.е. при
(т.е. при 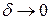 регуляризованное решение
регуляризованное решение 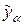 должно стремиться к точному решению
должно стремиться к точному решению 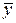 ).
).
Заметим, что во-первых, ниоткуда не следует единственность регуляризатора для данной задачи, а во-вторых, требование 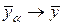 при
при 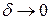 имеет только теоретическое значение, поскольку уровень
имеет только теоретическое значение, поскольку уровень 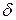 погрешностей исходных данных не может быть уменьшен по желанию вычислителя.
погрешностей исходных данных не может быть уменьшен по желанию вычислителя.
Всякая задача вида (4.16), для которой существует регуляризирующий оператор, называется регуляризуемой (или регуляризируемой), а всякий метод, порождающий такой оператор, называется методом регуляризации. Фигурирующая определении 4.5 скалярная величина  называется параметром регуляризации.
называется параметром регуляризации.
Одним наиболее универсальных способов построения регуляризирующих алгоритмов является метод 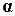 -регуляризации Тихонова. Суть его в следующем.
-регуляризации Тихонова. Суть его в следующем.
Пусть в уравнении (4.16)  – линейный вполне непрерывный оператор (т.е. любое ограниченное множество из
– линейный вполне непрерывный оператор (т.е. любое ограниченное множество из 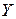 переводится им в компактное множество из
переводится им в компактное множество из 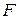 ),
), 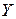 и
и 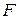 – гильбертовы пространства, и пусть вместо «точного» уравнения (4.16) известно приближенное уравнение
– гильбертовы пространства, и пусть вместо «точного» уравнения (4.16) известно приближенное уравнение
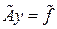 , (4.18)
, (4.18)
где 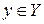 ,
, 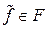 , а близость (4.16) и (4.18) характеризуется неравенствами
, а близость (4.16) и (4.18) характеризуется неравенствами
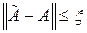 ,
, 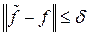 (4.19)
(4.19)
При поиске решения уравнения (4.16) на базе уравнения (4.18) вместо минимизации невязки 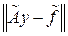 предлагается минимизировать так называемый сглаживающий функционал (функционал Тихонова)
предлагается минимизировать так называемый сглаживающий функционал (функционал Тихонова)
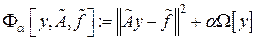 . (4.20)
. (4.20)
Здесь 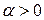 – параметр регуляризации, а
– параметр регуляризации, а 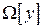 – стабилизирующий функционал (стабилизатор), главное требование к нему – неотрицательность; чаще всего, берут
– стабилизирующий функционал (стабилизатор), главное требование к нему – неотрицательность; чаще всего, берут 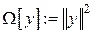 . Доказано, что функционал Тихонова, в частности,
. Доказано, что функционал Тихонова, в частности,
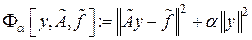 (4.21)
(4.21)
всегда имеет и притом единственный элемент 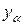 такой, что
такой, что
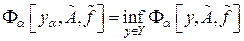 .
.
Нахождение оптимальных значений параметра 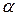 в общем случае представляет собой сложную задачу. Но для линейных алгебраических систем имеются простые прикидки для значений параметра
в общем случае представляет собой сложную задачу. Но для линейных алгебраических систем имеются простые прикидки для значений параметра 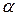 и точности приближения нормального псевдорешения
и точности приближения нормального псевдорешения 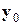 регуляризованным решением
регуляризованным решением 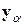 при таких
при таких 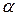 . Например, считается, что если в оценках (4.19) близости систем (4.16) и (4.18)
. Например, считается, что если в оценках (4.19) близости систем (4.16) и (4.18) 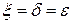 , то регуляризированное решение
, то регуляризированное решение 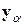 системы (4.18) приближает нормальное псевдорешение системы (4.16) с точностью
системы (4.18) приближает нормальное псевдорешение системы (4.16) с точностью 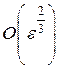 при
при 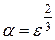 , если эта система разрешима, и с точностью
, если эта система разрешима, и с точностью 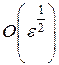 при
при 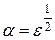 , если она не разрешима.
, если она не разрешима.
ГЛАВА 5. РЕШЕНИЕ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ СИСТЕМ (ПРЯМЫЕ МЕТОДЫ)
ВВЕДЕНИЕ
Методы решения линейных алгебраических задач (систем линейных алгебраических уравнений (СЛАУ), вычисление определителей, обращения матриц, вычисление собственных чисел) делятся на два класса:
1) прямые (точные) методы, обеспечивающие решение задач за конечное число арифметических операций. При точной реализации операций решение будет так же точным;
2) итерационные методы, в которых точное решение задачи достигается за бесконечное число итераций.
Рассмотрим СЛАУ вида:
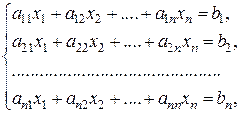 (5.1)
(5.1)
или иначе, векторно-матричных уравнений
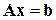 , (5.1а)
, (5.1а)
где 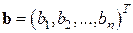 – вектор свободных членов и
– вектор свободных членов и 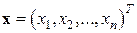 – вектор неизвестных (он же в другой интерпретации может означать и вектор-решение) с вещественными координатами, а
– вектор неизвестных (он же в другой интерпретации может означать и вектор-решение) с вещественными координатами, а 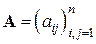 – вещественная
– вещественная 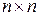 -матрица коэффициентов данной системы. Предполагается существование единственного решения системы (5.1). Эффективность способов решения системы (5.1) во многом зависит от структуры и свойств матрицы
-матрица коэффициентов данной системы. Предполагается существование единственного решения системы (5.1). Эффективность способов решения системы (5.1) во многом зависит от структуры и свойств матрицы 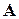 : размера, обусловленности, симметричности количества нулевых элементов и их расположения и т.д.
: размера, обусловленности, симметричности количества нулевых элементов и их расположения и т.д.
Применение аналитических методов решения СЛАУ таких, как формула Крамера

или с использованием обратной матрицы
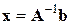
требует вычисления 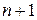 определителя.
определителя.
Известно, что при вычислении определителя  -мерной матрицы требуется выполнить
-мерной матрицы требуется выполнить 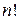 Операций умножения. Поэтому применение этих формул при расчете на ЭВМ не выгодно.
Операций умножения. Поэтому применение этих формул при расчете на ЭВМ не выгодно.
