Вопрос 1: Испытание. Множество элементарных событий. Случайные события. Операции над событиями. Алгебра событий

Опытом (испытанием) называется совокупность условий, которая может быть повторена любое число раз.

С каждым опытом должны связываться события, о которых можно сказать осуществились они или нет.

Невозможным событием называется событие, которое в результате опыта не может произойти.

Достоверным событием называют событие, которое в результате опыта обязано произойти.

Пространство элементарных событий — множество 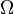всех различных исходов случайного эксперимента. Элемент этого множества 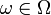называется элементарным событием или исходом. Пространство элементарных событий называется дискретным, если число его счётно. Любое пространство элементарных событий не являющееся дискретным, называется недискретным, и при этом, если наблюдаемыми результатами (нельзя произносить случайными событиями) являются точки того или иного числового арифметического или координатного пространства, то пространство называется непрерывным

Примеры

Примеры пространств исходов эксперимента, 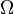, и элементарных событий:

-Если объекты счётны, а пространство исходов 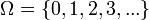(натуральные числа), то элементарные события — это любые множества 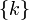, где .

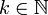-Если монета бросается дважды, , 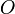для орла, а 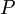для решки, то элементарные события: 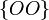, , 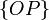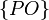и .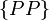

Случайное событие — подмножество множества исходов случайного эксперимента; при многократном повторении случайного эксперимента частота наступления события служит оценкой его вероятности.

Случайное событие, которое никогда не реализуется в результате случайного эксперимента, называется невозможным и обозначается символом 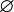. Случайное событие, которое всегда реализуется в результате случайного эксперимента, называется достоверным и обозначается символом .

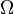Операции над событиями:

1.Суммой события называется событие, если осуществляется хотя бы одно из этих событий.

2.Произведением события называется событие, если осуществляется оба эти события.

3.Дополнение (отрицание) осуществляется, если событие А не осуществляется.

4.Разность двух событий – если одно из них не осуществляется.

События А и В называются несовместными, если их произведение есть невозможное событие.

Алгебра событий (в теории вероятностей) — алгебра подмножеств пространства элементарных событий 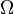, элементами которого служат элементарные события.

Как и положено алгебре множеств алгебра событий содержит невозможное событие (пустое множество) и замкнута относительно теоретико-множественных операций, производимых в конечном числе. Достаточно потребовать, чтобы алгебра событий была замкнута относительно двух операций, например, пересечения и дополнения, из чего сразу последует её замкнутость относительно любых других теоретико-множественных операций. Алгебра событий, замкнутая относительно счётного числа теоретико-множественных операций, называется сигма-алгеброй событий.