Эквивалентные системы линейных уравнений
Две системы линейных уравнений от одного набора x1,..., xn неизвестных и соответственно из m и p уравнений
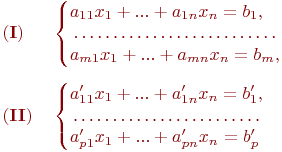
называются эквивалентными, если их множества решений 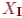 и
и 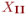 совпадают (т. е. подмножества
совпадают (т. е. подмножества 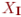 и
и 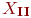 в Kn совпадают,
в Kn совпадают,  ). Это означает, что: либо они одновременно являются пустыми подмножествами
). Это означает, что: либо они одновременно являются пустыми подмножествами  (т. е. обе системы (I) и (II) несовместны), либо они одновременно непустые
(т. е. обе системы (I) и (II) несовместны), либо они одновременно непустые 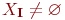 ,
, 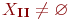 и
и 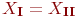 (т. е. каждое решение системы I является решением системы II и каждое решение системы II является решением системы I).
(т. е. каждое решение системы I является решением системы II и каждое решение системы II является решением системы I).
Элементарные преобразования систем линейных уравнений (строк матриц)
Определение 3.4.1 (элементарное преобразование 1-го типа). При 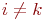 к i -му уравнению системы прибавляется k -е уравнение, умноженное на число
к i -му уравнению системы прибавляется k -е уравнение, умноженное на число 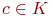 (обозначение: (i)'=(i)+c(k) ; т. е. лишь одно i -е уравнение (i) заменяется на новое уравнение (i)'=(i)+c(k) ). Новое i -е уравнение имеет вид (ai1+cak1)x1+...+(ain+cakn)xn=bi+cbk, или, кратко,
(обозначение: (i)'=(i)+c(k) ; т. е. лишь одно i -е уравнение (i) заменяется на новое уравнение (i)'=(i)+c(k) ). Новое i -е уравнение имеет вид (ai1+cak1)x1+...+(ain+cakn)xn=bi+cbk, или, кратко,
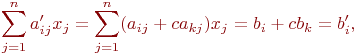
т. е. в новом i -м уравнении aij'=aij+cakj, bi'=bi+cbk.
Определение 3.4.2 (элементарное преобразование 2-го типа). При 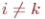 i -е и k -е уравнение меняются местами, остальные уравнения не изменяются (обозначение: (i)'=(k), (k)'=(i) ; для коэффициентов это означает следующее: для j=1,...,n
i -е и k -е уравнение меняются местами, остальные уравнения не изменяются (обозначение: (i)'=(k), (k)'=(i) ; для коэффициентов это означает следующее: для j=1,...,n

| 53. Метод Гаусса решения систем линейных уравнений | |||||||||||||||||||
Формулы Крамера и матричный метод решения систем линейных уравнений не имеют серьезного практического применения, так как связаны с громоздкими выкладками. Практически для решения систем линейных уравнений чаще всего применяется метод Гаусса, состоящий в последовательном исключении неизвестных по следующей схеме. Для того чтобы решить систему уравнений выписывают расширенную матрицу этой системы 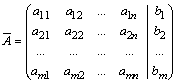 и над строками этой матрицы производят элементарные преобразования, приводя ее к виду, когда ниже главной диагонали, содержащей элементы и над строками этой матрицы производят элементарные преобразования, приводя ее к виду, когда ниже главной диагонали, содержащей элементы 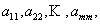 будут располагаться нули. Разрешается: 1) изменять порядок строк матрицы, что соответствует изменению порядка уравнений; 2) умножать строки на любые отличные от нуля числа, что соответствует умножению соответствующих уравнений на эти числа; 3) прибавлять к любой строке матрицы другую, умноженную на отличное от нуля число, что соответствует прибавлению к одному уравнению системы другого, умноженного на число. С помощью этих преобразований каждый раз получается расширенная матрица новой системы, равносильной исходной, т. е. такой системы, решение которой совпадает с решением исходной системы. Рассмотрим метод Гаусса на примерах. Пример 14. Установить совместность и решить систему будут располагаться нули. Разрешается: 1) изменять порядок строк матрицы, что соответствует изменению порядка уравнений; 2) умножать строки на любые отличные от нуля числа, что соответствует умножению соответствующих уравнений на эти числа; 3) прибавлять к любой строке матрицы другую, умноженную на отличное от нуля число, что соответствует прибавлению к одному уравнению системы другого, умноженного на число. С помощью этих преобразований каждый раз получается расширенная матрица новой системы, равносильной исходной, т. е. такой системы, решение которой совпадает с решением исходной системы. Рассмотрим метод Гаусса на примерах. Пример 14. Установить совместность и решить систему 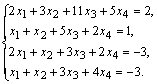 Решение. Выпишем расширенную матрицу системы и поменяем местами первую и вторую строки для того, чтобы элемент Решение. Выпишем расширенную матрицу системы и поменяем местами первую и вторую строки для того, чтобы элемент 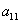 равнялся единице (так удобнее производить преобразования матрицы). равнялся единице (так удобнее производить преобразования матрицы). 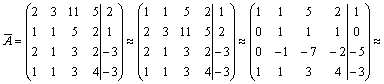 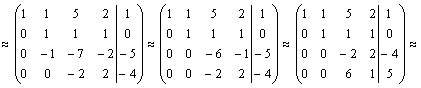 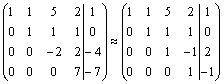 . Имеем . Имеем 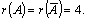 Ранги матрицы системы и ее расширенной матрицы совпали с числом неизвестных. Согласно теореме Кронекера-Капелли система уравнений совместна и решение ее единственно. Выпишем систему уравнений, расширенную матрицу которой мы получили в результате преобразований: Ранги матрицы системы и ее расширенной матрицы совпали с числом неизвестных. Согласно теореме Кронекера-Капелли система уравнений совместна и решение ее единственно. Выпишем систему уравнений, расширенную матрицу которой мы получили в результате преобразований: 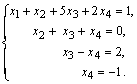 Итак, имеем Итак, имеем 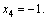 Далее, подставляя Далее, подставляя 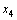 в третье уравнение, найдем в третье уравнение, найдем 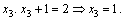 Подставляя Подставляя 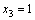 и и 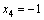 во второе уравнение, получим во второе уравнение, получим 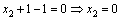 и, наконец, подставляя в первое уравнение найденные и, наконец, подставляя в первое уравнение найденные 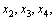 получим получим 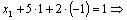 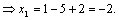 Таким образом, имеем решение системы Таким образом, имеем решение системы 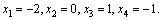 54. Однородные системы линейных уравнений Однородной системой m линейных уравнений с n неизвестными называется система вида 54. Однородные системы линейных уравнений Однородной системой m линейных уравнений с n неизвестными называется система вида
Эта система может быть записана в виде матричного уравнения
и операторного уравнения
Система (1) всегда совместна, так как: имеет очевидное решение x10 = x20 = … = xn0 = 0 , которое называется нулевым, или тривиальным; добавление нулевого столбца не меняет ранга матрицы, следовательно, выполняется достаточное условие теоремы Кронекера–Капелли; θ О Img ^A , так как Img ^A — линейное пространство. Естественно, нас интересуют нетривиальные решения однородной системы. Условие нетривиальной совместности: Для того, чтобы однородная система имела нетривиальное решение, необходимо и достаточно, чтобы ранг ее основной матрицы был меньше числа неизвестных. Доказательство см. в книге О.В. Зиминой ``Линейная алгебра и аналитическая геометрия", стр. 77. Следствие. Для того, чтобы однородная система n линейных уравнений с n неизвестными (матрица системы A — квадратная) имела нетривиальное решение, необходимо и достаточно, чтобы определитель матрицы этой системы был равен нулю ( det A = 0 ). Общим решением системы линейных уравнений называется формула, которая определяет любое ее решение. Так как система (1) эквивалентна операторному уравнению (2), то множество всех ее решений есть ядро оператора ^A . Пусть Ker ^A ≠ θ , Rg ^A = r и x1, x2, … , xn − r — базис в ядре оператора. Фундаментальной системой решений однородной системы (1) называется базис ядра оператора ^A (точнее, координатные столбцы базисных векторов в Ker ^A ). Это определение можно сформулировать несколько иначе: Фундаментальной системой решений однородной системы (1) называется n − r линейно независимых решений этой системы. Будем обозначать координатные столбцы базисных векторов в Ker ^A X1, X2, … , Xn − r . Теорема о структуре общего решения однородной системы уравнений: Любое решение однородной системы линейных уравнений определяется формулой
где X1, X2, … , Xn − r — фундаментальная система решений однородной системы линейных уравнений и C1, C2, … , Cn − r — произвольные постоянные. Свойства общего решения однородной системы уравнений: При любых значениях C1, C2, … , Cn − r X , определяемое формулой (3), является решением системы (1). Каково бы ни было решение X0 , существуют числа C10, … , Cn − r0 такие, что
Вывод: Чтобы найти фундаментальную систему и общее решение однородной системы, нужно найти базис ядра соответствующего линейного оператора. Наши рекомендации
|
