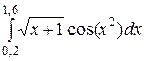Тіктөртбұрыштар әдісі.
Тіктөртбұрыштар әдісі сандық интегралдау әдістерінің ең қарапайым түрі болып табылады. Бұл әдісте анықталған интегралды тікелей (5.1.2) интегралдық қосындымен алмастырып, 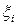 нүктесі ретінде
нүктесі ретінде 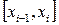 ,
, 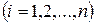 - қарапайым кесінділердің сол жақ
- қарапайым кесінділердің сол жақ 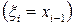 немесе оң жақ
немесе оң жақ  шекараларын алуға болады.
шекараларын алуға болады. 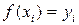 деп белгілеп, осы екі жағдайлар үшін тіктөртбұраштар әдісінің келесі квадратурлық формулаларын аламыз:
деп белгілеп, осы екі жағдайлар үшін тіктөртбұраштар әдісінің келесі квадратурлық формулаларын аламыз:
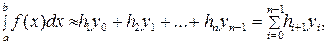 (5.1.4)
(5.1.4)
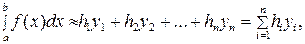 (5.1.5)
(5.1.5)
(5.1.4) – сол жақ тіктөртбұрыштар формуласы, ал (5.1.5) – оң жақ тіктөртбұрыштар формуласы деп аталады. Интегралдық қосындыда 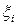 нүктесі ретінде қарапайым кесіндінің ортасын
нүктесі ретінде қарапайым кесіндінің ортасын 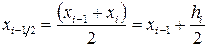 ,
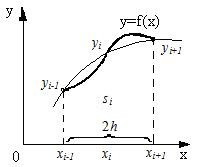
, 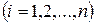 алу арқылы (5-суретке қара), (5.1.4), (5.1.5) формулаларға қарағанда дәлірек болатын, келесі түрдегі тіктөртбұрыштар формуласын алуға болады:
алу арқылы (5-суретке қара), (5.1.4), (5.1.5) формулаларға қарағанда дәлірек болатын, келесі түрдегі тіктөртбұрыштар формуласын алуға болады:
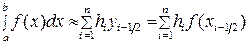 (5.1.6)
(5.1.6)
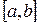 кесіндісін бірдей n бөлікке бөлген кезде, яғни
кесіндісін бірдей n бөлікке бөлген кезде, яғни 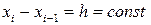
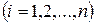 болғанда (5.1.4), (5.1.5) (5.1.6) формулалары сәйкесінше келесі түрде болады:
болғанда (5.1.4), (5.1.5) (5.1.6) формулалары сәйкесінше келесі түрде болады:
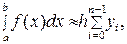 (5.1.4¢)
(5.1.4¢)
 (5.1.5¢)
(5.1.5¢)
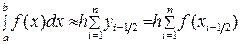 , (5.1.6¢)
, (5.1.6¢)
мұндағы 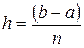 - қадам.
- қадам.
Мысал 1. Сол жақ және оң жақ тіктөртбұрыштар формулаларын қолданып 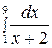 интегралды шешу керек, n=4.
интегралды шешу керек, n=4.
Шешуі. Бұл интегралды Ньютон-Лейбниц формуласы арқылы оңай есептеп, дәл мәнін анықтауға болады:
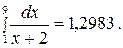
Енді берілген интегралды тіктөртбұрыштар әдісін қолданып есептейік. Интегралдың a=1; b=9 шектерін біле отырып, 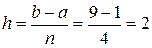 қадамды анықтаймыз. Онда
қадамды анықтаймыз. Онда
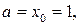
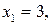
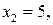
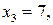
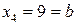 ,
,
ал осы нүктелерде интеграл астындағы 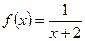 функцияның мәні
функцияның мәні

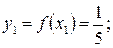
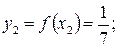
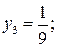
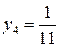
тең болады. Алдымен интегралды есептеу үшін сол жақ тіктөртбұрыштар формуласын қолданайық. Қадам тұрақты болғандықтан (5.1.4¢) формуласы арқылы интегралдың сандық мәнін аламыз:
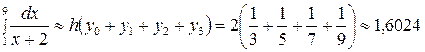 .
.
(5.1.5¢) – оң жақ тіктөртбұрыштар формуласын қолдансақ:
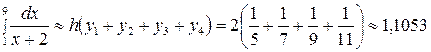 .
.
Ал (5.1.6¢) формуласын қолдану үшін қарапайым кесінділердің 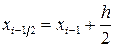 - ортасын және сол нүктелердегі интеграл астындағы функцияның
- ортасын және сол нүктелердегі интеграл астындағы функцияның 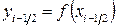
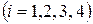 мәндерін анықтау керекпіз:
мәндерін анықтау керекпіз:
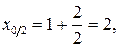
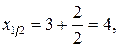
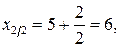
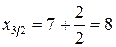 .
.
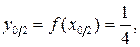
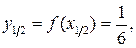
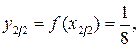
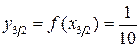 . Онда
. Онда
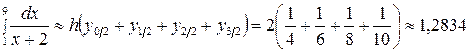 .
.
Осы нәтижелерден берілген интеграл үшін (5.1.6¢) формуласы дәлірек шешім беретінін көруге болады.
Тіктөртбұрыштар әдісінің қателігін бағалау. 5-суретте көрсетілгендей ізделінді қисықсызықты трапецияның ауданы тіктөртбұрыштар аудандарының қосындысы ретінде жуықтап анықталады. Әр қарапайым кесіндіде
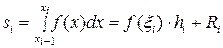 , (5.1.7)
, (5.1.7)
ал  кесіндісінде аудан
кесіндісінде аудан
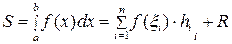 (5.1.8)
(5.1.8)
тең болады. Егер қарапайым кесінділердегі 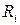 және
және  кесіндідегі
кесіндідегі 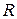 қателіктерді ескермесек, онда жоғарыда көрсетілген тіктөртбұрыштар әдісінің квадратурлық формулаларын аламыз.
қателіктерді ескермесек, онда жоғарыда көрсетілген тіктөртбұрыштар әдісінің квадратурлық формулаларын аламыз.
Бұл формулаларды қолдану үшін 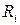 және
және 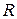 қателіктер шамаларын бағалау керек.
қателіктер шамаларын бағалау керек. 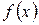 функциясы
функциясы 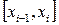
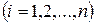 кесіндіде өзінің бірінші және екінші ретті туындыларымен үзіліссіз болсын.
кесіндіде өзінің бірінші және екінші ретті туындыларымен үзіліссіз болсын. 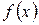 функциясының алғашқы функциясы ретінде,
функциясының алғашқы функциясы ретінде, 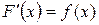 болатын,
болатын, 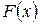 функциясын алып,
функциясын алып,
(5.1.7) формуласының сол жағын келесі түрде жазайық
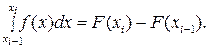 (5.1.9)
(5.1.9)
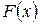 функциясын
функциясын 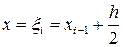 нүктесінің маңайында Тейлор қатарына жіктесек, функцияның
нүктесінің маңайында Тейлор қатарына жіктесек, функцияның 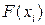 және
және 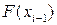 мәндерін аламыз:
мәндерін аламыз:
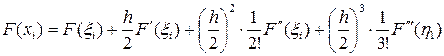 , (5.1.10)
, (5.1.10)
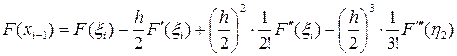 , (5.1.11)
, (5.1.11)
мұндағы 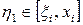 , ал
, ал 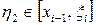 . (5.1.9) формуланың оң жағына (5.1.10) және (5.1.11) өрнектерін қоя отырып және
. (5.1.9) формуланың оң жағына (5.1.10) және (5.1.11) өрнектерін қоя отырып және 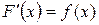 ескере отырып,
ескере отырып,
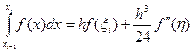 (5.1.12)
(5.1.12)
қатынасын аламыз, мұндағы 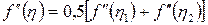 (
( 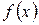 функциясының үзіліссіз болғандықтан мұндай
функциясының үзіліссіз болғандықтан мұндай 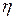 шамасы бар болады). (5.1.12) формуладағы соңғы мүше тіктөртбұрыштар әдісінің (5.1.6¢) квадратурлық формуласының әр қарапайым кесіндідегі
шамасы бар болады). (5.1.12) формуладағы соңғы мүше тіктөртбұрыштар әдісінің (5.1.6¢) квадратурлық формуласының әр қарапайым кесіндідегі 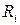 қателігін береді:
қателігін береді:
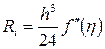 . (5.1.13)
. (5.1.13)
(5.1.8) формуладағы 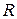 қателік, яғни анықталған интегралдың (5.1.6¢) квадратурлық формуламен есептеудегі
қателік, яғни анықталған интегралдың (5.1.6¢) квадратурлық формуламен есептеудегі 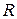 қателігі
қателігі 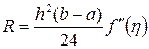 ,
, 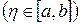 тең болады. Бұл шама (5.1.13) формуласын
тең болады. Бұл шама (5.1.13) формуласын 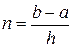 шамасына көбейткеннен шығады. Екінші ретті туындысы бар
шамасына көбейткеннен шығады. Екінші ретті туындысы бар 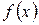 - интеграл астындағы функция үшін
- интеграл астындағы функция үшін 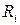 және
және 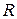 қателіктері h қадамды азайтқан сайын кемитіні көрінеді.
қателіктері h қадамды азайтқан сайын кемитіні көрінеді.
Тапсырма. 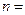 10 болғанда оң және сол тікбұрыштар формулалары бойынша интегралды есептеңдер. Алынған нәтижелердің дәлдігін бағалаңдар.
10 болғанда оң және сол тікбұрыштар формулалары бойынша интегралды есептеңдер. Алынған нәтижелердің дәлдігін бағалаңдар.
1) 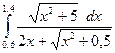 2)
2) 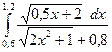 3)
3) 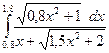
4) 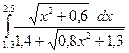 5)
5) 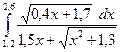
Трапеция әдісі.
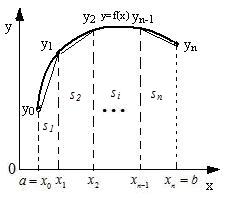 Трапеция әдісінде сызықты интерполяция қолданады, яғни
Трапеция әдісінде сызықты интерполяция қолданады, яғни 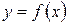 функциясының графигі
функциясының графигі 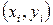 нүктелерін қосатын түзулер түрінде сипатталады.Бұл жағдайда қисықсызықты трапецияның ауданы, яғни анықталған интегралдың мәні жуық шамамен қарапайым тікбұрышты трапециялардың si аудандарының қосындысы ретінде анықталады (6-сурет).
нүктелерін қосатын түзулер түрінде сипатталады.Бұл жағдайда қисықсызықты трапецияның ауданы, яғни анықталған интегралдың мәні жуық шамамен қарапайым тікбұрышты трапециялардың si аудандарының қосындысы ретінде анықталады (6-сурет).
6-сурет
Әр қарапайым трапецияның ауданы 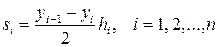 тең. Осы теңдіктерді i бойынша қоссақ,
тең. Осы теңдіктерді i бойынша қоссақ,
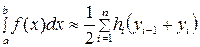 (5.1.14)
(5.1.14)
формуласын аламыз. Бұл формуланы трапеция формуласы деп атайды.
Трапеция формуласының қателігі 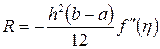 формуласы түрде анықталады, мұндағы
формуласы түрде анықталады, мұндағы 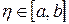 . Егер
. Егер 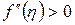 болса, онда (5.1.14) формуласы анықталған интегралдың дәл мәнімен салыстырғанда артық мәнді береді, ал егер
болса, онда (5.1.14) формуласы анықталған интегралдың дәл мәнімен салыстырғанда артық мәнді береді, ал егер 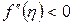 болса, онда (5.1.14) – трапеция формуласы анықталған интегралдың дәл мәнімен салыстырғанда кем мәнді береді.
болса, онда (5.1.14) – трапеция формуласы анықталған интегралдың дәл мәнімен салыстырғанда кем мәнді береді.
Кесінділердің ұзындықтары тұрақты, яғни 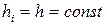 болған жағдайда
болған жағдайда 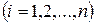 трапеция формуласы келесі түрде болады:
трапеция формуласы келесі түрде болады:
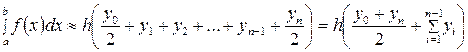 (5.1.15)
(5.1.15)
Мысал 2. 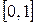 кесіндісін бірдей он бөлікке бөліп: n=10, тіктөртбұрыштар формуласын және трапеция формуласын пайдаланып,
кесіндісін бірдей он бөлікке бөліп: n=10, тіктөртбұрыштар формуласын және трапеция формуласын пайдаланып, 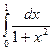 анықталған интегралын есептеңдер. Қателікті бағалаңдар.
анықталған интегралын есептеңдер. Қателікті бағалаңдар.
Шешуі.Бұл интегралды Ньютон-Лейбниц формуласы арқылы оңай есептеп, дәл мәнін анықтауға болады:
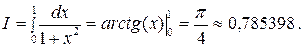
Енді тіктөртбұрыштар және трапеция формуласын пайдаланып, интегралды есептейік. Ол үшін 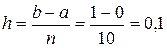 қадамды анықтап.
қадамды анықтап. 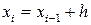 және
және 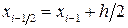
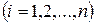 нүктелердегі
нүктелердегі 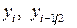 - интеграл астындағы функцияның мәнін есептейік (1-кесте):
- интеграл астындағы функцияның мәнін есептейік (1-кесте):
4.1-кесте
| i | 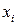 | 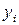 | 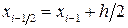 | 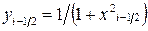 |
| 0,1 | 0,990099 | 0,05 | 0,9975506 | |
| 0,2 | 0,961538 | 0,15 | 0,977995 | |
| 0,3 | 0,917431 | 0,25 | 0,941176 | |
| 0,4 | 0,862069 | 0,35 | 0,890868 | |
| 0,5 | 0,8 | 0,45 | 0,831601 | |
| 0,6 | 0,735294 | 0.55 | 0,767754 | |
| 0,7 | 0,671141 | 0,65 | 0,702988 | |
| 0,8 | 0,609756 | 0,75 | 0,64 | |
| 0,9 | 0,552486 | 0,85 | 0,580552 | |
| 0,5 | 0,95 | 0,525624 |
Онда (5.1.6¢) – тіктөртбұрыштар әдісінің формуласын пайдаланып,
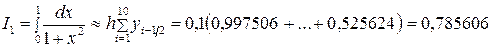
аламыз. Бұл жағдайда интегралды есептеу қателігі 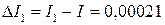 (шамамен 0,027%) тең.
(шамамен 0,027%) тең.
(5.1.15) – трапеция формуласын қолданып,
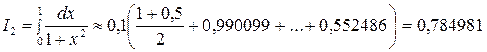 аламыз. Дәл мән белгілі болған жағдайда интегралды есептеу қателігі
аламыз. Дәл мән белгілі болған жағдайда интегралды есептеу қателігі 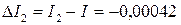 (шамамен 0,054%) тең. Сонымен, қарастырылып отырған мысалда интегралды есептеудің дәлірек мәнін тіктөртбұрыштар формуласы бергенін көруге болады. (5.1.6¢) – тіктөртбұрыштар формуласының дәлірек мән беруі si аудандарын есептеу тәсіліне байланысты, яғни қарапайым фигуралардың ауданын есептеген кезде
(шамамен 0,054%) тең. Сонымен, қарастырылып отырған мысалда интегралды есептеудің дәлірек мәнін тіктөртбұрыштар формуласы бергенін көруге болады. (5.1.6¢) – тіктөртбұрыштар формуласының дәлірек мән беруі si аудандарын есептеу тәсіліне байланысты, яғни қарапайым фигуралардың ауданын есептеген кезде 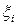 нүктесі ретінде
нүктесі ретінде 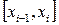 кесіндінің ортасын алғанға байланысты. Бұл есепте (5.1.4¢) және (5.1.5¢) тіктөртбұрыштар формулаларын қолдансақ, қателік 3% артық болатынын ескере кетейік.
кесіндінің ортасын алғанға байланысты. Бұл есепте (5.1.4¢) және (5.1.5¢) тіктөртбұрыштар формулаларын қолдансақ, қателік 3% артық болатынын ескере кетейік.
Тапсырмалар.Трапеция формуласын пайдаланып, интегралды есептеңдер:
1) 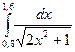 2)
2) 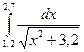 3)
3)  4)
4) 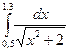 5)
5) 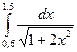 .
.
4. Симпсон әдісі (Парабола әдісі).Көптеген есептерде  кесіндісін қарапайым кесінділерге бөлетін
кесіндісін қарапайым кесінділерге бөлетін 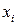
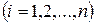 нүктелері берілген кезде және сандық интегралдау дәлдігін hi қадамды азайту арқылы жоғарылату келмейтін кезде, яғни функция кесте түрінде берілген жағдайда интеграды есептеу керек болады. Сондықтан бұл жағдайда тіктөртбұрыштар және трапеция формулаларына қарағанда жоғары дәлдікті беретін квадратурлық формулаларды қолданған жөн. Осындай әдістердің бірі – Симпсон әдісі болып табылады. Бұл әдісте дәлдікті жоғарылату интерполяция дәлдігін жоғарылатумен жүзеге асады, яғни
нүктелері берілген кезде және сандық интегралдау дәлдігін hi қадамды азайту арқылы жоғарылату келмейтін кезде, яғни функция кесте түрінде берілген жағдайда интеграды есептеу керек болады. Сондықтан бұл жағдайда тіктөртбұрыштар және трапеция формулаларына қарағанда жоғары дәлдікті беретін квадратурлық формулаларды қолданған жөн. Осындай әдістердің бірі – Симпсон әдісі болып табылады. Бұл әдісте дәлдікті жоғарылату интерполяция дәлдігін жоғарылатумен жүзеге асады, яғни 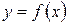 функциясы екінші дәрежелі Лагранж көпмүшелігімен алмастырылады (квадраттық интерполяция).
функциясы екінші дәрежелі Лагранж көпмүшелігімен алмастырылады (квадраттық интерполяция).
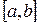 интегралдау кесіндісін қадамы h болатын n жұп бөлікке бөлейік. Әр
интегралдау кесіндісін қадамы h болатын n жұп бөлікке бөлейік. Әр  ,
, 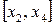 , ...,
, ...,  ,...,
,..., 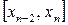 кесіндіде интеграл астындағы
кесіндіде интеграл астындағы 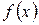 функциясын екінші дәрежелі интерполяциялық көпмүшелікпен алмастырамыз:
функциясын екінші дәрежелі интерполяциялық көпмүшелікпен алмастырамыз:
7-сурет
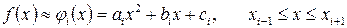 . Бұл квадраттық үшмүшенің коэффициенттерін көпмүшеліктің
. Бұл квадраттық үшмүшенің коэффициенттерін көпмүшеліктің 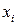 нүктелердегі мәні сәйкесінше функцияның
нүктелердегі мәні сәйкесінше функцияның 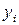 мәндеріне тең болу шарттарынан алуға болады. Жоғарыда айтқанымыздай
мәндеріне тең болу шарттарынан алуға болады. Жоғарыда айтқанымыздай 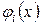 ретінде
ретінде 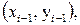
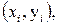
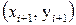 нүктелері арқылы өтетін екінші дәрежелі Лагранж көпмүшелігін алуға болады:
нүктелері арқылы өтетін екінші дәрежелі Лагранж көпмүшелігін алуға болады:
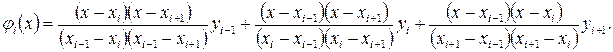
7-суреттегі қарапайым фигураның 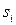 ауданын анықталған интеграл арқылы есептеуге болады.
ауданын анықталған интеграл арқылы есептеуге болады. 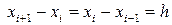 теңдігін ескере отырып,
теңдігін ескере отырып,
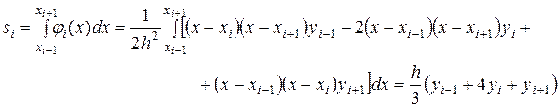
аламыз. Осындай есептеулерді әр 
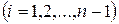 қарапайым кесінді үшін жүргізсек, қисықсызықты трапецияның ауданын, яғни
қарапайым кесінді үшін жүргізсек, қисықсызықты трапецияның ауданын, яғни 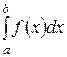 анықталған интегралдың жуық мәнін аламыз:
анықталған интегралдың жуық мәнін аламыз:
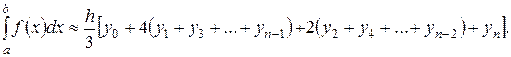 (5.1.16)
(5.1.16)
(5.1.16) формуласы - Симпсон формуласы деп аталады.
Бұл әдістің қателігі 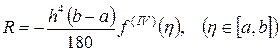 формуласымен анықталады. Осыдан Симпсон әдісі тіктөртбұраштар мен трапеция әдістерімен салыстырғанда дәлірек екені байқалады.
формуласымен анықталады. Осыдан Симпсон әдісі тіктөртбұраштар мен трапеция әдістерімен салыстырғанда дәлірек екені байқалады.
Сонымен қатар, Симпсон формуласын басқа тәсілдермен, мысалы тіктөртбұраштар формуласы мен трапеция формуласын бірге немесе трапеция әдісін екі рет пайдаланып, Ньютон интерполяциялық көпмүшелікті қолдана отырып алуға болады.
Мысал 3.Симпсон формуласы арқылы жоғарыда қарастырылған (мысал 2) интегралды есептейік: 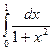 .
.
Шешуі. Интеграл астындағы функцияның n=10, 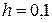 кездегі мәндері 1-кестеде берілген. Онда (5.1.16) формуласын қолдана отырып
кездегі мәндері 1-кестеде берілген. Онда (5.1.16) формуласын қолдана отырып
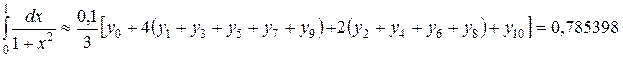
интегралдың дәл мәніне тең болатынын аламыз.
Тапсырмалар.
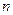 =8 болғанда Симпсон формуласымен интегралды есептеу.
=8 болғанда Симпсон формуласымен интегралды есептеу.
1) 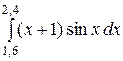 2)
2) 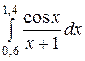 3)
3) 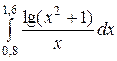
4) 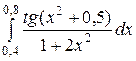 5)
5)