Графи і відношення

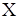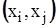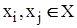Нехай на безлічі задане бінарне відношення А. Йому відповідає орієнтований граф, вершини якого відображають елементи з X, а дуга , де , існує тоді і тільки тоді, коли 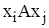. Обернено, множина орієнтованих дуг графа (без строго рівнобіжних дуг), заданих упорядкованими парами 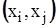, можна розглядати як бінарне відношення на безлічі X. Якщо бінарне відношення встановлює зв'язок між елементами х із безлічі Х и елементами y із безлічі Y ( 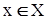, 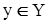), то граф такого відношення буде орієнтованим биграфом.

Варто помітити, що в загальному випадку орграф представляє щось більше, ніж бінарне відношення. Будь-яке бінарне відношення, визначене на деякій безлічі, можна представити відповідним орграфом, вершини якого відповідають елементам цієї безлічі. Однак орграф із рівнобіжними дугами дозволяє відбивати більш загальні зв'язки між об'єктами, чим бінарні відношення.