Спосіб заміни площин проекцій

В результаті проведення заняття студент повинен:

- ЗНАТИ алгоритми рішення основних задач способом заміни площин проекцій.

- ВМІТИ розв’язувати метричні задачі способом заміни площин проекцій.

Питання до опрацювання теми які виносяться на МК1

1. З якою метою застосовується метод переміни площин проекцій?

2. У чому сутність способу переміни площин проекцій?

3. Які типи задач розв’язуються переміною однієї з площин проекцій?

4. В яких задачах доводиться застосовувати послідовну заміну двох площин проекцій?

Аудиторні завдання

1 Визначити відстань від точки А до площини ∑ (ВС // ЕD).

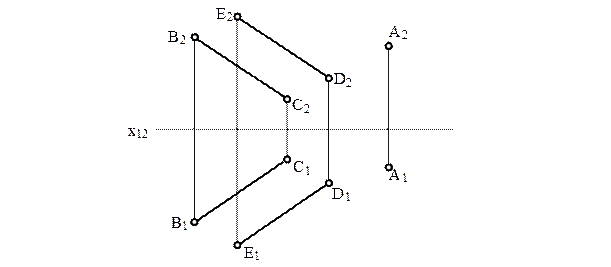
2 Визначити відстань між мимобіжними прямими m і n.

3 *Побудувати горизонтальну проекцію вершини D за умови, що двогранний кут при ребрі АВ дорівнює 30⁰.

4 *Побудувати проекцію квадрату ABCD, якщо АС – його діагональ, а кут нахилу площини квадрату до П₂ дорівнює 25⁰.

5 *Побудувати фронтальну проекцію АВ // CD, віддалену від CD

на 20 мм.

Завдання до самостійного опрацювання

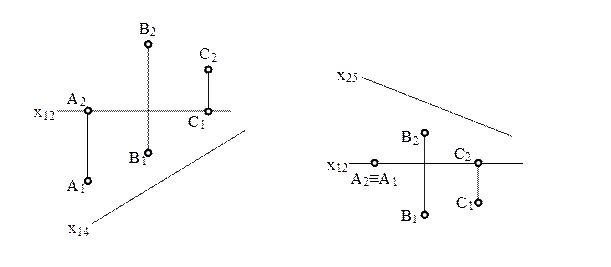
1 Побудувати проекції точок А, В і С на площини П₄ і П₅.

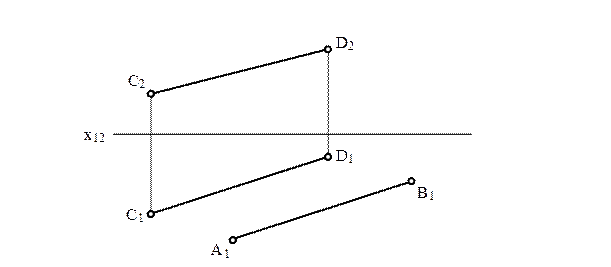
2 Визначити відстань між паралельними прямими.

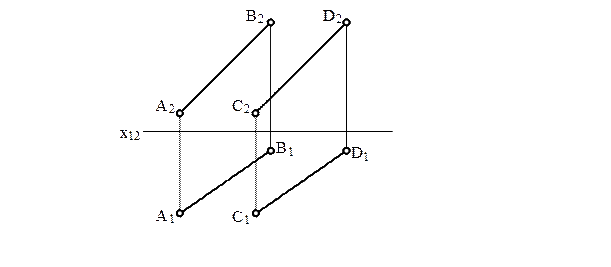
3 Визначити відстань між точкою А та прямою ВС.

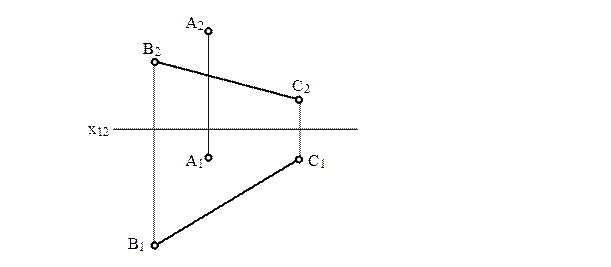
4 Визначити кути нахилу площин а) ∑ (∆АВС) до площини П₁ та б) Θ (h⁰×f⁰) до площини П₂.

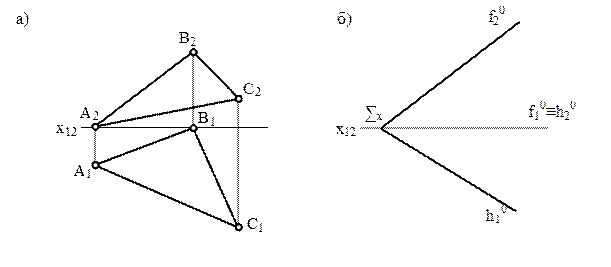
5 Визначити натуральну величину трикутника АВС.

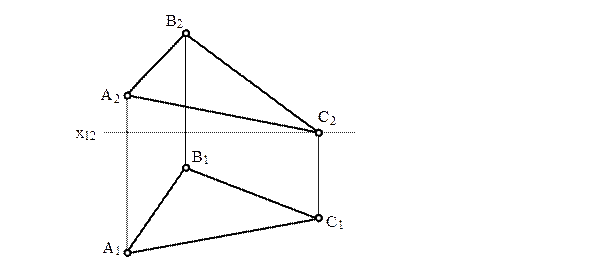
6 Визначити величину двогранного кута при ребрі АВ.

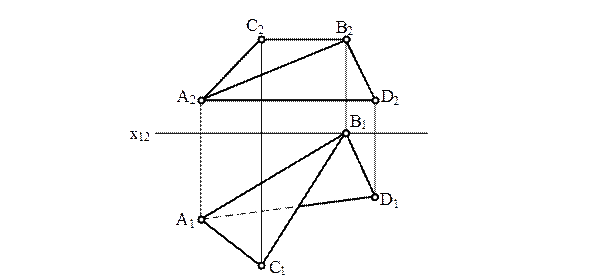
Модульний контроль 1

Заняття 9

ТЕМА: Способи перетворення комплексного креслення.

Спосіб плоскопаралельного переміщення

В результаті проведення заняття студент повинен:

- ЗНАТИ алгоритми рішення основних задач способом плоскопараллельного переміщення проекцій.

- ВМІТИ розв’язувати метричні задачі способомплоскопараллельного переміщення проекцій.

Питання до опрацювання теми які виносяться на МК1

1. З якою метою застосовується метод плоскопараллельного переміщення проекцій?

2. У чому сутність способу плоскопараллельного переміщення проекцій?

3. Які типи задач розв’язуються способом плоскопараллельного переміщення проекцій?

Аудиторні завдання

1 Визначити відстань між мимобіжними прямими.

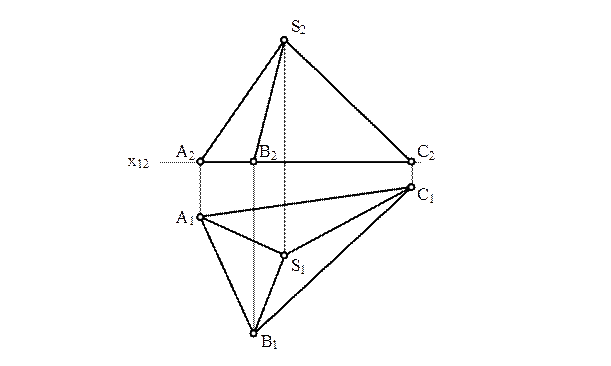
2 Визначити величину двогранного кута при ребрі піраміди AS.

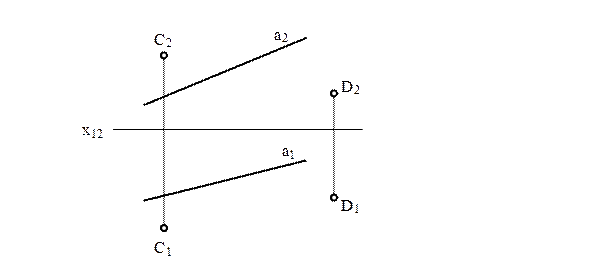
3 Провести пряму, паралельну прямим АВ і CD, віддалену від АВ на

20 мм, а від CD на 15 мм.

4 Побудувати пряму b//a і рівновіддалену від точок C i D.

5 *Побудувати C₂D₂, якщо CD//AB, а відстань між ними дорівнює 20 мм.

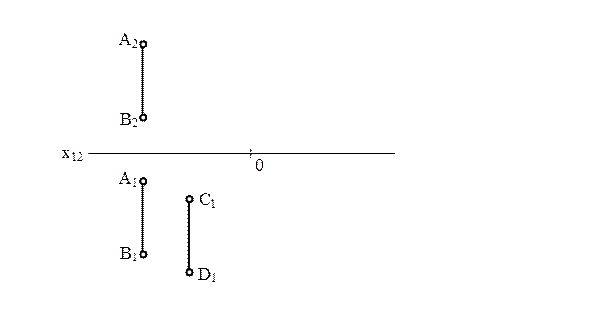
Завдання до самостійного опрацювання

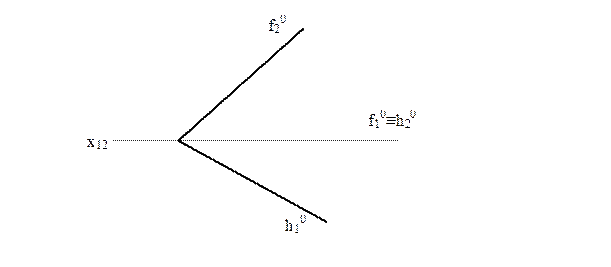
1 Визначити кут нахилу площини ∑ (h⁰×f⁰) до фронтальної площини проекції.

2 Визначити відстань між паралельними площинами і кут нахилу їх до площини П₂.

3 Визначити натуральну величину грані піраміди ASB.

Модульний контроль 1

Заняття 10