Тема: ИЗУЧЕНИЕ ОСНОВНЫХ ПАРАМЕТРОВ КОЛЕБАТЕЛЬНЫХ СИСТЕМ

ЦЕЛЬ РАБОТЫ:освоить методы расчета параметров колебаний маятника с использованием измеренных значений частоты колебаний, длины маятника, жесткости пружины, квазиупругих сил.

ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: комбинированный маятник, секундомер, линейка.

КРАТКАЯ ТЕОРИЯ

Повторяющиеся движения или изменения состояния называются колебаниями. Наиболее простой формой колебаний является гармоническое колебание, т.е. такое при котором колеблющаяся величина изменяется во времени по закону синуса или косинуса.

Колебания бывают свободные и вынужденные, затухающие и незатухающие, периодические и непериодические.

Свободными называют колебания, которые происходят в системе при выведении ее из равновесия без воздействия внешних сил. Вынужденными называют колебания, которые происходят в системе при выведении ее из равновесия под действием внешних периодических сил.

Рассмотрим свободные гармонические незатухающие колебания.

Данный вид колебаний описывается дифференциальным уравнением второго порядка следующего вида:

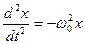(1)

а его решение имеет вид:

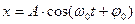(2)

где А – амплитуда колебаний, ω₀ – круговая частота колебаний, φ₀ – начальная фаза колебаний.

Смещение (x) – отклонение колеблющейся системы от положения равновесия в любой момент времени (м).

Амплитуда (A или а) – максимальное смещение колеблющейся системы от положения равновесия (м).

Период колебания (T) – время одного полного колебания (с).

Частота колебаний (ν) – количество колебаний за период (1/с).

Фаза колебаний (φ) – угол между радиус-вектором и осью OX (градус):

,

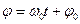где φ₀ – начальная фаза колебаний.

Частота колебаний ν и период Т связаны между собой соотношением:

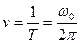(3)

Для наблюдения гармонических колебаний в физике используются маятники различного типа: пружинный, математический и физический.

Пружинный маятник – это груз массой m, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы

F= - kx, где k – коэффициент упругости, в случае пружины называемый жесткостью.

Математический маятник – это идеализированная система, состоящая из материальной точки массой m, подвешенной на нерастяжимой невесомой нити, и колеблющаяся под действием силы тяжести. Хорошим приближением математического маятника является небольшой тяжелый шарик, подвешенный на тонкой длинной нити.

Физический маятник – это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси подвеса, не проходящей через центр масс тела.

Для пружинного, математического и физического маятников период колебаний рассчитывается по формулам:

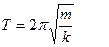
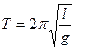(4)

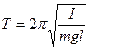
где I – момент инерции физического маятника, l – приведенная длина маятника, k – коэффициент жесткости пружины, m – масса материальной точки.

Для затухающих свободных гармонических колебаний дифференциальное уравнение второго порядка имеет вид:

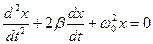(5)

А его решение

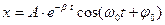(6)

где β – коэффициент затухания.

ХОД РАБОТЫ

I. Определение параметров колебаний комбинированного маятника.

1) Закрепить комбинированный маятник горизонтально (α=00) на штативе (рис.1). 2) Отклонить маятник от положения равновесия на расстояние х (см. таблицу вариантов) и определить время 10 полных колебаний. Измерения повторить не менее трёх раз. 3) Рассчитать время одного колебания – период Т.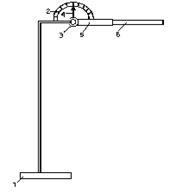
Рис.1

4) Определить угловую частоту ω колебаний маятника используя формулу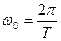

5) Закрепить маятник на штативе под углом α = -30, -45, -60 и -90 градусов и повторить пункты 2-4 в каждом из положений не менее трёх раз. Данные занести в таблицу.

6) По полученным данным построить график зависимости угловой частоты от угла ω(α).

7) Определить коэффициент квазиупругих сил k_ку при каждом угле α (параметры маятника m и l см. рис. 2)

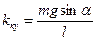
8) Определить коэффициент упругости k_у только при α=0⁰

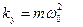
9) Оценить упругие, квазиупругие и суммарные силы, действующие на маятник при отклонении его от положения равновесия на х см по формулам:

; ;

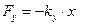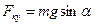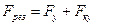
10) Полученные данные занести в таблицу 1.

Таблица 1.

α, град	Т, с	ω, рад/с	kу, Н/м	kку, Н/м	Fу, Н	Fку, Н	Fрез, Н
-30
-45
-60
-90
90┴

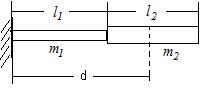
Рис. 2

Параметры маятника:

m₁=6,5 г; m₂=60,73 г; l₁=140 мм; l₂=230 мм.

Таблица вариантов для задания

Вариант	I	II	III	IV
х, см

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что называется колебанием?

2. Назовите основные виды колебаний.

3. Что такое гармоническое колебание? Величины, характеризующие гармонические колебания (период, частота, смещение от положения равновесия, амплитуда, фаза), их физический смысл и единицы измерения.

4. Дифференциальное уравнение свободных незатухающих колебаний и его решение.

5. Дифференциальное уравнение свободных затухающих колебаний и его решение. Логарифмический декремент затухания.

6. Дифференциальное уравнение вынужденных колебаний и его решение.

7. Скорость и ускорение при гармоническом колебательном движении.

8. Энергия (кинетическая, потенциальная, полная) гармонического колебательного движения.

Лабораторная работа № 4