Абсолютна й відносна похибки
Тригонометричні функції
План
1. Наближені значення і похибка наближень. Запис наближень.
2. Округлення чисел. Похибка округлення.
3. Похибка обчислень з наближеними даними
Деякі відомості про наближені обчислення й похибки
Розв’язок прикладних і математичних задач, як правило, пов'язане з наближеними значеннями величин, наближеними обчисленнями.
Математична модель задачі — це вже наближене подання реального об'єкта. Вихідні дані, одержувані з експерименту, можна в основному визначити лише приблизно. Навіть точні числа, такі як 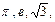
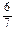 і т.п., при обчисленнях заміняють десятковими дробами, залишаючи певне число знаків після коми.
і т.п., при обчисленнях заміняють десятковими дробами, залишаючи певне число знаків після коми.
Обчислювальні методи в основному також є наближеними. Навіть при використанні найпростішої формули результат, як правило, одержують наближеним.
Тому, перш ніж приступитися до вивчення обчислювальних методів, варто ознайомитися із загальними правилами дій над наближеними числами й оцінки похибок.
Абсолютна й відносна похибки
Абсолютна похибка наближеного числа. Якщо а0 — деяке число (відоме точно або не точно), а а — число, прийняте за наближене значення числа а0, то помилкою наближеного числа а називають різницю а0 — а. Звичайно точне число а0 не відомо, тому помилку наближеного числа а визначити не можна. Однак майже завжди можна вказати число, що оцінює цю помилку. Число 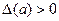 , що задовольняє нерівності
, що задовольняє нерівності
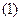 |а0 - а| <
|а0 - а| < 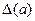 ,
,
називається абсолютною похибкою (точніше граничною абсолютною похибкою) наближеного числа а.
Очевидно, таке визначення абсолютної похибки не є однозначним. Так, якщо а = 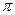 , а за наближене значення взяти а = 3,14, то, з огляду на те, що 3,140 <
, а за наближене значення взяти а = 3,14, то, з огляду на те, що 3,140 < 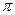 < 3,142, можна записати
< 3,142, можна записати
| 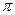 — а |< 0,002, |
— а |< 0,002, | 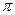 — а |< 0,01, |
— а |< 0,01, | 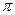 — а |< 0,1.
— а |< 0,1.
Кожне із чисел 0,002, 0,01, 0,1 буде абсолютною похибкою числа а. Але чим ближче між собою числа |а0 — а|й 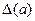 , тим точніше абсолютна похибка оцінює фактичну помилку.
, тим точніше абсолютна похибка оцінює фактичну помилку.
Як абсолютна похибка 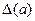 наближеного числа а беруть по можливості найменше із чисел, що задовольняють нерівності (1).
наближеного числа а беруть по можливості найменше із чисел, що задовольняють нерівності (1).
Нерівність (1) рівносильна нерівностям
а — 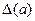
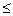 а0
а0 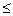 а +
а + 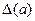 ,
,
які умовно записують у такий спосіб: а0 = а ± 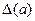 , тобто а0 приблизно дорівнює а з абсолютною похибкою
, тобто а0 приблизно дорівнює а з абсолютною похибкою 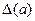 . Так, наприклад, у попередньому прикладі можна записати
. Так, наприклад, у попередньому прикладі можна записати 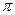 = 3,14 ± 0,002.
= 3,14 ± 0,002.
Абсолютну похибкою іноді називають оцінкою точності наближеного числа.
Відносна похибка наближеного числа. Абсолютна похибка 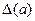 числа а, прийнятого за наближене значення числа а0, не завжди є зручною характеристикою степеня точності а як наближення до а0. Похибка в один метр є дуже грубою помилкою при вимірі довжини приміщення, але її можна розглядати як малу помилку при вимірі відстані між двома вилученими крапками земної поверхні. Отже, крім величини абсолютної похибки, необхідно ще знати її відношення до вимірюваного (або що обчислює) величині, в основному виражає у відсотках.
числа а, прийнятого за наближене значення числа а0, не завжди є зручною характеристикою степеня точності а як наближення до а0. Похибка в один метр є дуже грубою помилкою при вимірі довжини приміщення, але її можна розглядати як малу помилку при вимірі відстані між двома вилученими крапками земної поверхні. Отже, крім величини абсолютної похибки, необхідно ще знати її відношення до вимірюваного (або що обчислює) величині, в основному виражає у відсотках.
Відносною похибкою наближеного числа а називається відношення абсолютної похибки 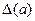 до модуля цього числа. Відносна погрішність позначається через
до модуля цього числа. Відносна погрішність позначається через 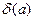 :
:
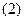
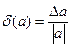
або у відсотках
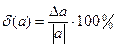 .
.
Так, відносна похибка числа 3,14, прийнятого за наближене значення числа 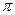 , при
, при 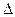 (3,14) = 0,002 дорівнює
(3,14) = 0,002 дорівнює
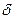 (3,14) =
(3,14) = 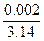 = 0,00064, або 0,064 %.
= 0,00064, або 0,064 %.
У технічних розрахунках точність вимірів звичайно характеризують відносною похибкою. Результат вважають хорошим, якщо відносна похибка не перевищує 0,1 %.
З формули (2) слідує, що
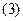
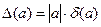 .
.
Правило округлення чисел
Округлення числа полягає у відкиданні в ньому всіх цифр, що випливають за деяким розрядом. При цьому якщо округлене число ціле, то відкинуті цифри цілої частини заміняють нулями.
Округлення звичайно роблять за наступним правилом.
Якщо перша відкинута цифра, менше п'яти, то попередня цифра не міняється.
Якщо перша відкинута цифра, більше п'яти, то попередня цифра збільшується на одиницю.
Якщо перша відкинута цифра, дорівнює п'яти, то придатне кожне із зазначених правил, але найчастіше округляють так, щоб остання зберігаєма цифра, була парною. Якщо вона непарна, то до неї додають одиницю, якщо ж парна, то залишають без змін (правило парної цифри).
Приклад 1. Округлити число 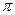 = 3,14159... до а) одного; б) трьох; в)чотирьох десяткових знаків.
= 3,14159... до а) одного; б) трьох; в)чотирьох десяткових знаків.
а) 3,14159  3,1 (округлення до 0,1);
3,1 (округлення до 0,1);
б) 3,14159  3,142 (округлення до 0,001);
3,142 (округлення до 0,001);
в) 3,14159  3,1416 (округлення до 0,0001).
3,1416 (округлення до 0,0001).
При округленні цілих чисел звичайно замість відкинутих цифр записують не нулі, а число 10 у відповідному степені.
Приклад 2. Округлити число 246250 до а) сотень тисяч; б) десятків тисяч; в) сотень.
а) 246250  2
2 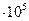 (округлення до
(округлення до 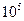 );
);
б) 246250  25
25 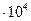 (округлення до 104);
(округлення до 104);
в) 246250  2462
2462 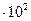 (округлення до 102).
(округлення до 102).
Степінь числа 10 указує на число округлених знаків.
Якщо при округленні числа останні зберігають нулі, то їх варто записувати. Так, число 1,2997, округлене до 0,001, приймає вид 1,300.
При округленні числа виникає додаткова похибка — похибка округлення 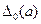 , що не перевершує половини одиниці розряду останньої цифри, що зберігається (або п'яти одиниць першого відкинутого розряду).
, що не перевершує половини одиниці розряду останньої цифри, що зберігається (або п'яти одиниць першого відкинутого розряду).
Так, у прикладах 1, 2 маємо наступні похибки округлення;
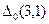 =0,04159
=0,04159 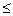 0,05,
0,05, 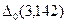 =0,00041
=0,00041 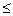 0,0005;
0,0005; 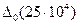 =3750
=3750 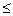 0,5
0,5 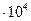 .
.
Абсолютна похибка округленого числа є сума його первісної абсолютної похибки й похибки округлення. Наприклад, нехай 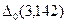 = 0,2, при округленні 3,142 до 0,1 одержуємо 3,1 й
= 0,2, при округленні 3,142 до 0,1 одержуємо 3,1 й 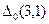 = 0,042, тоді
= 0,042, тоді 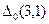 = 0,2 + +0,042 = 0,242. Звичайно абсолютну й відносну похибки округляють до однієї, рідше до двох цифр, відмінних від нуля. Округлення похибок роблять тільки у бік збільшення до тих же розрядів, що й наближене число. Так, при
= 0,2 + +0,042 = 0,242. Звичайно абсолютну й відносну похибки округляють до однієї, рідше до двох цифр, відмінних від нуля. Округлення похибок роблять тільки у бік збільшення до тих же розрядів, що й наближене число. Так, при 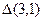 = 0,242 розуміють
= 0,242 розуміють 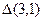 = 0,3.
= 0,3.
