Существенное значение для работы системы АПЧ при больших расстойках имеет также форма скатов детекторной характеристики. 5 страница

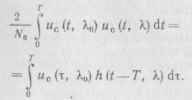(11.32)

Это условие выполняется, когда импульсная характеристика СФ связана с опорным сигналом «_с (/, к) коррелятора соотношением

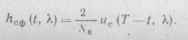(11.33) 222

Из сказанного следует, что во всех схемах оптимальных Прм вместо когерентных корреляторов с опорными сигналами и_с (/, к) можно применять СФ с импульсной характеристикой (11.33) и добавлением ключа, подключающего выходной сигнал СФ (11.31) к РУ в момент времени t - Т окончания наблюдения. При этом на выходах коррелятора и СФ возникает одинаковое максимально возможное энергетическое отношение сигнал/шум д_аы% (Т) 2 Э_сШ_в 130].

Рассмотрим квадратурные корреляционные приемники для сигналов с неизвестной начальной фазой. При этом когерентный прием по схеме рис. 11.4 становится невозможным, так как создать опорное напряжение, когерентное с точностью до фазы, нельзя. В этих случаях, как отмечалось, приходится прибегать к квадратурной процедуре обработки смеси с ортогональными по фазе опорными напряжениями (см. рис. 11.5, 11.6) с формированием на выходе оптимального Прм эффекта Q (к) или нелинейной функции от него. Поясним физический смысл этой процедуры, а заодно найдем альтернативные решения для квадратурных оптимальных Прм.

Заменим в схеме рис. 11.5 корреляторы согласованными фильтрами с импульсными характеристиками

сопряженными по

формуле (11.33) с соответствующими опорными сигналами (11.19). В результате приходим к альтернативной схеме оптимального Прм (рис. 11.8). Найдем выходные напряжения согласованных фильтров

сделав при этом допущения: входной сигнал амплитудно-модулированный

U (г)cos (i£>₀tФо),

а шум отсутствует, т. е. х (t) s= w_c (t.

tpo). В этом случае импульсные характеристики СФ принимают вид

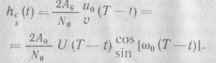
В результате выходные напряжения СФ в схеме рис. 11.8.

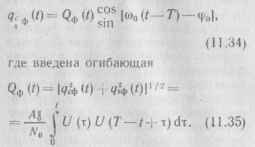
Выходной эффект формируется в виде г (t) In /„ IQ„, (01. При / = Т огибающая (11.35) достигает максимума:

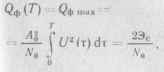
(11.36)

совпадающего с выходным эффектом А„ Q (к) в схеме квадратурного корреляционного приемника рис. 11.5. Взятие в качестве выходного эффекта

лишь огибающей является типичной некогерентной процедурой, так как при этом отказываются от высокочас тотной фазовой информации. Поэто му естественно заменить два СФ од ним, сопряженным с опорным сигна лом, равным сигнальному и_с (t, ф₀) но с произвольной фазой ф_оп. В ре зультате приходим к схеме оптималь ного фильтрового некогерентногс приемника (рис. 11.9). Она состоит из СФ с импульсной характеристикой вида

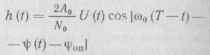
и нелинейного амплитудного детектора (АД), выделяющего нелинейную функцию 1п/₀ (<2_Ф) огибающей <3_Ф (t) на выходе СФ.

Можно сохранить огибающую ф_ф (0 при замене несущей частоты /о входного сигнала на промежуточную частоту /_п. Тогда получится схема так называемого оптимального корреляционно-фильтрового приемника (рис. 11.10).Она состоит из преобразователя частот (ПЧ) с идеальным колебательным контуром, настроенным на промежуточную частоту со_п и выполняющим роль интегратора. Огибающая на его выходе совпадает с огибающей фф (0 в схеме рис. 11.9. По-

этому выходная часть (амплитудный нелинейный детектор) оптимальных Прм рис. 11.9, 11.10 одинакова.

Схемы оптимальных Прм рис. 11.5, 11.8— 11.10 адекватны и широко используются при реализации оптимальных РПУ для сигналов с неизвестной начальной фазой и постоянной (не флуктуирующей) амплитудой. Для сигналов с флуктуирующей амплитудой процедура формирования огибающей <2_Ф (/) остается неизменной. Меняется лишь выходная часть в схемах рис. 11.8—11.10 в соответствии со схемой рис. 11.6.

§ 11.3. Оптимальная нелинейная фильтрация сообщений

Задача фильтрации и методы ее решения. Задача фильтрации является важнейшей составной частью статистической теории оптимального радиоприема сообщений. Сущность задачи фильтрации ясна из рис. 11.11,а. Здесь наблюдаемый процесс

х (t) является аддитивной смесью сигнала и_с It, X (г)] и шума и_т (г). В задачах оптимального приема функцией X (t) считают сообщение, или модулирующую функцию узкополосного сигнала, например: и_с It, X (t)\

X (t) cos [ы„ t — ф_п| — амплитудная модуляция, U_n cosI 0)_п/

—X (t) — ф₀] — угловая модуляция. В задачах измерений в радиолокации, радионавигации, радиоуправлении под функцией X (t) понимают физическую величину (дальность, скорость, пеленг), подлежащую измерению. В задачах вторичной и третичной обработки информации в радиотехнических системах различного назначения под функцией X (t) подразумевают само сообщение, т. е. полагают, что х (t) = X (t) + и_т (t).

Задачей оптимального фильтра (ОФ) (рис. 11.11, а) во всех этих случаях является наилучшее (в рамках заданного критерия оптимальности)

выделение оценки сообщения X {t) или какой-нибудь функции от нее

Если сигнал является линейной функцией от сообщения . и_с (t, X) —

— X (X), то фильтрация называется линейной, а сам ОФ синтезируется в классе оптимальных линейных фильтров (ОЛФ). К оптимальной линейной фильтрации относится амплитудная демодуляция, когда и_с (t, X) = = k (t) X (t), где k (t) = cos (м„/ —

— ф₀) — известная функция време-НИ-Фильтрация сообщения из смеси i х (t) — X (t) -j- и_ш (t) также является линейной и приводит к хорошо йз-

вестным ОЛФ Винера, Калмана — Бьюси и согласованным фильтрам.

Если зависимость u_c(t, Я) = § (X) — нелинейная (как при угловой: фазовой, частотной демодуляции), то I фильтрация считается нелинейной, а . ОФ рис. 11.11, а синтезируется в -классе оптимальных нелинейных фильтров (ОНФ).

Все перечисленные задачи целесо-| образно рассматривать с единых мате-' матических позиций как задачи о п-|т и м а л ь н о й нелинейной фильтрации, сводящиеся к оптимальной оценке функции времени

'.Я, (г), закодированной (в общем случае нелинейно) в наблюдаемом процессе х (f). При этом упомянутые задачи оптимальной линейной фильтрации (в том числе задачи Винера и Калмана — Бьюси) будут вытекать из этих решений как частные случаи.

Известны два методических подхода к решению задачи оптимальной нелинейной фильтрации [12].

1. Ф о р м и р о в а н и е текущей оценки. Здесь задания фиксированного интервала наблюдения О, Т (рис. 11.11, б) не требуется

и оценка X (/) вырабатывается непрерывно для любого текущего момента времени /е=7\Это эквивалентно формированию оценок на переменном (текущем) интервале наблюдения О,/. При этом применяется классический байесов подход из теории оценок векторных параметров X (см. § 11.2), сущность которого сводится к следующему.

Путем дискретизации по времени с шагом At функция X (г) на текущем интервале 0, t, == iAt (рис. 11.11, б) заменяется векторной случайной величиной Xi = \Х_г, Xj == (X (iAt)], а наблюдаемый процесс х (t) — векторной выборкой Х| = lx_lt Xt = — х (iAt)]. Теперь задачу оценки функции X (t) на интервале 0, / можно заме'нить задачей оценки векторной случайной величины X_t, закодированной в наблюдаемом процессе х (t). Эта задача в байесовой постановке решалась в§ 11.1, 11.2. Здесь в качест-

Я Зяк. lohS

ве оптимальной оценки X_t = [Я,, ...

Я,] целесообразно брать характерную точку (моду, медиану, центр тяжести) многомерной апостериорной плотности вероятностей;

p(Xi) = p(X_i/\_i) = p(X_l, .... Я,/*,, ...

-., x_i) = k_ip(X_t)p(X_i/X_i) =

= kp(X_l)L(X_l).(11.37)

Р. Л. Стратонович предложил использовать для вынесения оптимальной текущей оценки так называемую финальную одномерную апостериорную плотность вероятностей, связанную с (11.37) интегральным соотношением

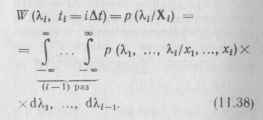
Если, например, в качестве оптимальной оценки выбрать центр тяжести функции (11.38), то оценка примет вид

(11.39)

Для получения следящих алгоритмов оптимальной нелинейной фильтрации необходимо составить рекуррентные уравнения, связывающие для двух гиседних выборок ti, t_i+l либо финальные апостериорные плотности вероятностей (11.38), либо сами оценки (11.39).

Первый метод использовал Р. Л. Стратонович. На основании допущения о марковости сообщения Я(/) ему в 1959—1960 гг. удалось найти рекуррентное уравнение для финальных апостериорных плотностей вероятностей (11.38), которое при предельном переходе At —*■ 0 привело к интегродифференциально-

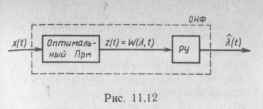
Рис. 11.12

му уравнению для плотностей вероятностей W {X, t) - lim W (X,, t_t).

Это уравнение называется уравнением оптимальной нелинейной фильтрации (по Стратоновичу).

Примерно в это же время, используя допущение о гауссовости сообщения X (О,И. А. Большаков и В. Г. Репин нашли рекуррентную связь

оценок (11.39) X_j+], X_t непосредственно. В предельном случае А/ —>- 0 эти рекуррентные уравнения свелись к интегродифференциальным уравнениям фильтрации из смеси х (г) не-

посредственно сообщения X (t) =

lim =- «ДО-

Марковская теория оптимальной нелинейной фильтрации (по Стратоновичу) свелась в общем случае к структурной схеме ОНФ, показанной на рис. 11.12. Схема содержит оптимальный Прм и решающее устройство (РУ). Первый путем решения уравнения оптимальной фильтрации формирует текущую финальную апостериорную плотность вероятности W (X, t). Решающее устройство формирует оценку X (0 в виде ее моды или центра тяжести. Преимуществом марковской теории оптимальной нелинейной фильтрации является возможность ее использования для негауссовых сообщений а (0 и шумов и_ш (0, что часто встречается в практических приложениях, в частности при приеме сигналов на фоне сильных шумовых помех.

Гауссова теория оптимальной нелинейной фильтрации (по Большакову и Репину) дает конкретную структуру ОНФ, формирующего непосредственно оценку X (t) из

наблюдаемого процесса х (0, минуя стадию вычисления финальной апостериорной плотности вероятностей. Требование гауссовости апостериорных плотностей вероятностей (11.37), (11.38) существенно снижает практическое применение этой теории. Как правило, ее используют в теории приема или высокоточных измерений в гауссовом шуме, когда исходные ограничения соблюдаются.

Тем не менее следует заметить, что марковская теория оптимальной нелинейности фильтрации дает физически наглядные результаты лишь в случае гауссовой аппроксимации финальной апостериорной плотности вероятностей (11.38). Этот частный случай так называемой квазиоптимальной теории нелинейной фильтрации, развитый В. И. Тихоновым 1301 и его учениками, приводит к структурным схемам ОНФ, близким к схемам, вытекающим из гауссовой теории.

2. Формирование оценки «в целом». Другой методический подход к оценке функции времени X (0 на интервале наблюдения 0, Т. предложенный Г. Ван-Трисом l.VM, Э. Витерби и рядом других авторов, сводится к следующему. Исходным допущением, как и в теории Большакова, Репина, является гауссовость сообщения X (0- Это позволяет аппроксимировать его каноническим разложением Карунена — Лоэва [301:

(11.40)

Здесь А= [а_ь a_r.....a_h\ — нормально-распределенная векторная случайная величина с взаимно-некоррелированными компонентами а_Г.

Детерминированные ортогональные функции if_r(0 выбирают по заданной корреляционной функции сообщения #_х (г, т) = < X (0 X (t + т)>. Применение канонического разложения переводит всю реализацию X (0, заданную «в целом» на интервале, наблюдения 0 < / < Т, в функцию слу-

чайного параметра А.т. е. Я (/) = =Я(г, А),/ £ О, Т. Это позволяет свести задачу оценки функции Я (г) «в целом» на всем интервале наблюдения О, Т к задаче оценки векторной случайной

величины А=[а_ь а_г, а_к].

Получив оценку А,нетрудно восстановить искомую оценку сообщения:

X(t) = limX(t), X (t) = К (t. А) =

(11.40а)

Принципиальное отличие такого подхода — невозможность использования текущей оценки. Здесь теоретически оценка Аможет быть вынесена лишь один раз, после окончания времени наблюдения t Т. Тогда восстановление оценки но алгоритму (11.40а) будет происходить в нереальном масштабе времени при ОТ. В результате возникает структура следящего ОНФ с нереализуемыми (в аналоговом виде) звеньями. Однако структурные схемы ОНФ в рамках данного подхода проще, чем при оптимальной нелинейной фильтрации с текущими оценками.

Ниже рассмотрим и сравним структурные схемы ОНФ, вытекающие из марковской и гауссовой теории с текущими оценками, а также гауссовой теории с оценкой «в целом».

Марковская теория оптимальной нелинейной фильтрации с текущей оценкой.В самом общем случае, как показал Р. Л. Стратонович, теория оптимальной нелинейной фильтрации применима тогда, когда взаимно-зависимые процессы х (/), Я (t) совместно образуют многомерный марковский процесс. При этом каждый из них — не обязательно марковский. Однако в практических приложениях теории оптимального приема 1301 наиболее распространен частный случай, когда Я (t) — простой марковский процесс диффузионного типа, а шум u_m (t) — белый гауссов шум со спектральной плотностью N „. Рассмотрим этот случай

подробнее, используя описанную м тодику формирования текущей оценки.

Для любого простого марковского процесса основной статистической характеристикой является вероятность перехода р (Я₍₊,/Я;), через которую записывается многомерная априорная плотность вероятностей:

P(h) = p(K.....К. К+х.....Я,-) =

= р(к_]) П р(К+./Ю- (П.41)

Допущение гауссовости белого шума позволяет представить (см. § 11.2) функцию правдоподобия в (11.37) н виде

(11.42)

где введена функция, связанная с

функционалом правдоподобия

,f [Я(/)| = р \х (/)/Я (t)\ соотношением

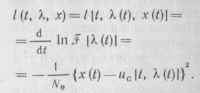(11.43)

Подставив (11.41), (11.42) в (11.37), запишем апостериорные плотности вероятностей для двух соседних выборок:

откуда следует рекуррентная формула р (Я_г+1)- с,₊, р (ki) р (*.( + ,/*.,) /. X X (a,_<+,)/Z. (Я,).Подставив это выра-

жение в (11.38), после интегрирования получим рекуррентную формулу для финальной апостериорной плотности вероятностей:

Коэффициент пропорциональности Cj ₊ , вычисляют из условия нормиров-

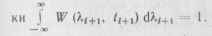
Для получения алгоритмов оптимальной нелинейной фильтрации при аналоговом приеме в формуле (11.44) обозначают л_; л (г) к, Х,₊₁

к (t -\- At) — Л (/ 4- т) к_х и переходят к пределу At—<-0. При этом используется дифференциальное уравнение для вероятности перехода р (л,/Х) простого марковского процесса, называемое уравнением Фок-кера — Планка — Колмогорова I30J;

называются соответственно коэффициентами сноса и диффузии. При этом статистическое усреднение производится по л_т при к = const, например:

X р (Ах/Х) dki. В результате из (11.44) вытекает следующее уравнение оптимальной нелинейной фильтрации (по Стратоновичу):

Здесь введена функция (11.43) и ее статистическое среднее по финальной апостериорной плотности вероятностей

В качестве начального условия уравнения фильтрации используется априорная плотность вероятностей начального значения сообщения р (к, t 0) = р,„.\к (0)1 при / = 0.

Первые два слагаемых в (11.47), эквивалентные правой части уравнения Фоккера — Планка -— Колмогорова (11.45), обязаны своим происхождением априорным сведениям о вероятности переходов сообщения к (г). Они влияют на апостериорную плотность вероятностей W (к, t), приводя ее к расширению с течением времени (увеличению неопределенности). Последнее слагаемое действует в обратном направлении (приводит к уменьшению неопределенности) за счет вновь приходящей информации, заложенной в функции правдоподобия.

Уравнение фильтрации (П-47) решается в оптимальном приемнике схемы рис. 11.12.

Следует отметить, что конкретный вид коэффициентов сноса и диффузии '

(11.46), их линейный или нелинейный характер зависят от принятой модели сообщения X (г) [30].

В табл. 11.1 приведены некоторые частные случаи простых марковских процессов диффузионного типа и выписаны их коэффициенты сноса и диффузии. Все эти процессы формируются из белого шума и удовлетворяют определенным стохастическим дифференциальным уравнениям, которые можно также представить в виде соответствующих структурных схем.

Перейдем к алгоритмам квазиоптимальной фильтрации в гауссовом приближении. Для этого постулируем финальную апостериорную плотность вероятностей в виде закона нормального распределения:

(11.49)

Математическое ожидание Х₀ (/)

совпадает с оптимальной оценкой X (t)

в схеме рис. 11.12, а о'{ (t) = D (t) соответствует дисперсии этой оценки и характеризует потенциальную точность оптимальной нелинейной фильтрации.

Подставим (11.49) в уравнение (11.47) и пренебрежем высшими производными а<и> = d^(|i)<H к , t) ^ _ dk*

b(l, t) ₀ _

= ■-й-- при и > 2. Тогда полу-

дк»

чим два дифференциальных уравнения оптимальной нелинейной фильтрации для процессов k(t), D (t):

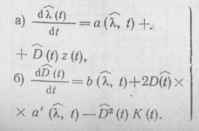
(11.50)

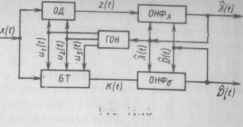
Рис. 11.13

Здесь а' (к, t) d а (X, t)/dk и введены две функции, связанные с функцией (19.43) соотношениями

Штрихи указывают номер произ-

водной функции u_c\t, к (:)] по X (/).

Уравнения оптимальной нелинейной фильтрации (11.50) реализуются с помощью структурной схемы рис. 11.13. Она состоит из пяти блоков.

Первый блок, который называют 113) оптимальным дискриминатором (ОД), в соответствии с алгоритмом (11.51) формирует выходной эффект г (г)- Структурная схема ОД показана на рис. 11.14. Входным напряжением является напряжение смеси х (/) = и_с I/, X (01 + и_ш (t). Для работы ОД требуются первые два из трех опорных напряжений:

Таблица 11.1

Тип марковского процесса Я (/)	Стохастическое дифференциальное уравнение	Схема формирования процесса	Коэффициент сноса а а. п	и диффузии Ь (Я.,о
Винеровский процесс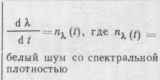
Нормальный процесс с экспоненциальной корреляцией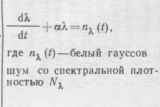
Обобщенный марковский диффузионный процессе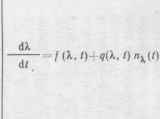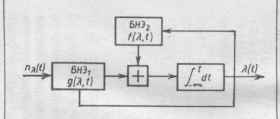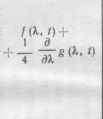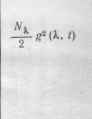
Рэлеевский марковский процесс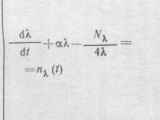

Рис. 11.14

вырабатываемых вторым блоком — генератором опорных напряжений (ГОН) на основе обратной связи по

оценке X (г).

Третий блок, называемый обычно блоком точности (БТ), формирует в качестве выходного эффекта функцию К (0> определяемую алгоритмом (11.52). Структурная схема БТ показана на рис. 11.15. Для его работы требуются три опорных напряжения (11.53).

Остальные два блока являются оптимальными нелинейными фильтрами. Первый из них (ОНФх) в соответствии с алгоритмом (11.50а) из входного напряжения г (t) и двух выходных эффектов X {t), D (г) формирует искомую оценку X (t). Структурная схема ОНФ*, показана на рис. 11.16. Нелинейность этого фильтра задается в общем случае нелинейной зависимостью а (X), реализуемой с помощью безынерционного нелинейного элемента (БНЭ): Лишь в частном случае (см. табл. 11.1, строка 2) гауссова марковского сообщения X (t) фильтр становится линейным. Второй оптимальный нелинейный фильтр (ОНФ„) в соответствии с алгоритмом (11.50 б) из входного напряжения К (t) и двух выход-

ных эффектов X (i), D (t) формир

выходной эффект D (t). Структур! схема ОНФ₀ несколько сложнее с мы ОНФ), (см. рис. 11.16).

Конкретный вид опорных нап жений (11.53) существенно влияет структуру ОД и БТ и определяе видом модуляции. В табл. 11.2 п ведены опорные напряжения для р личных видов модуляции. Структ; ОНФх, ОНФ₀ зависит в основном статистической структуры сооб: ния X (г), т. е. от вида коэффицен сноса и диффузии, приведенных табл. 11.1.

Конкретные примеры ОНФ, текающих из марковской теории тимальной нелинейной фильтраи приведены в гл. 15.

Гауссова теория оптимальной линейной фильтрации стеку! оценкой.Если в смеси х (г) = и х|г, X (г)] + и_шЦ) сигнала с бе. гауссовым шумом сделать допущет что сообщение X(t) является гау< вым с нулевым математическим о; данием < X (/) > = 0 и задан корреляционной функцией R%. (t, 1 = < X (t) X (т) >, то многомер; апостериорный закон распределе (11. 37) можно записать в явном bi используя по-прежнему функ: правдоподобия (11.42). Найдя в ном виде плотности вероятно» (11.37), (11.38) и оценку (11. Большакову и Репину уда; получить рекуррентное уравне]

^—-

связывающее оценки Х_г+1 в со ние моменты времени. В резулк предельного перехода t\t -*■ 0б

Таблица 11.2

получено уравнение оптимальной нелинейной фильтрации:

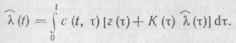
(11.54)

Здесь функции z (t), К (t) по-прежнему определены формулами (11.51), (11.52), а функция с (/, т) является решением интегрального уравнения