Анализ точности в установившемся режиме

Пусть система описывается дифференциальным уравнением .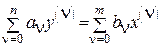

В момент времени 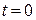на вход системы поступает воздействие x(t) и система при этом в момент времени 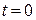имеет ненулевые начальные условия (наличие в системе запасенной энергии, порожденной действием предыдущего сигнала, поступившего на систему до t = 0). Введем новые понятия.

Сигнал 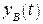, порожденный входным воздействием 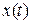, поступившим на систему в момент 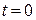, называется вынужденным движением (вынужденными колебаниями) системы;

Сигнал 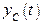, порожденный ненулевыми начальными условиями, называется свободным движением (свободными колебаниями) системы.

Выходной сигнал системы будет иметь вид: .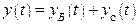

Изображение выходного сигнала с учётом правила дифференцирования оригинала при ненулевых начальных условиях будет иметь следующий вид:

.

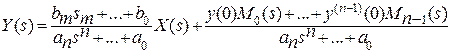Первое слагаемое учитывает влияние внешнего воздействия, второе слагаемое - эффект действия ненулевых начальных условий.

Рассмотрим вынужденный сигнал при нулевых начальных условиях и 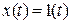. Изображение выходного сигнала имеет вид:

.

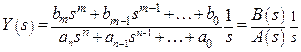Выходной сигнал, соответствующий 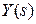, имеет вид:

,

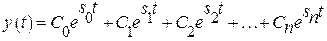где 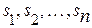– корни уравнения А(s) = 0 (полюса системы);

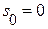– нулевой корень, порожденный воздействием .

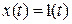Введем понятия установившегося (статического) и неустановившегося (динамического) режимов работы системы.

Составляющая 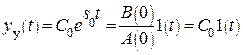порождена полюсом воздействия х(t)=1(t) и называется установившимся сигналом.

Составляющая 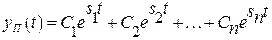порождена полюсами передаточной функции и называется переходным сигналом.

Эта составляющая определяет динамические свойства системы, т.к. с физической точки зрения порождена инерционностью системы.

Формулы для расчета 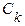имеют вид: , .

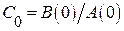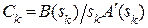
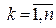Т.о., вынужденный сигнал состоит из двух составляющих .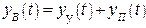

Режим, при котором составляющая 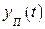отлична от нуля, называется неустановившимся или переходным(динамическим).

Режим, при котором 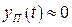, называется установившимся или статическим.

Т.о., выходной сигнал может быть записан 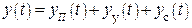, где

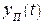– сигнал, порожденный полюсами передаточной функции системы;

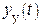– сигнал, порожденный полюсами входного воздействия;

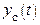– сигнал, порожденный ненулевыми начальными условиями.

Рис. 7. Выходной сигнал системы при x(t) = 1(t)

Разностьмежду входным и выходным сигналом называется ошибкой системы, т.е. .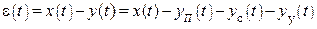

Ошибка системы при условии, что 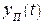и 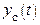отличны от нуля, называется переходной или динамической.

Ошибка системы, определяемая формулой 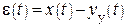, при условии, что 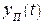и 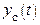стремятся к нулю, называется установившейся или статической.

Разность между максимальным отклонением при 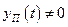и статическим отклонением представляет собой динамическое отклонение.

Для определения ошибки в установившемся режиме необходимо уметь вычислять передаточные функции системы при поступлении на неё воздействий, разных по виду и месту воздействия.

Рассмотрим типовую одноконтурную систему управления, на которую поступает 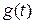задающее воздействие, содержащее цель управления, и возмущение :

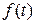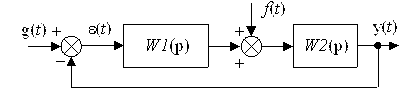
Определим передаточные функции системы для разных воздействий и приведём формулы упрощённого вычисления передаточных функций.

Передаточная функция прямой цепи по задающему воздействию 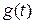при ( ).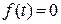

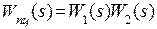
1. Передаточная функция разомкнутой системы по 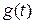при ( ).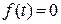

,

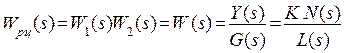где 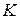- общий коэффициент усиления,

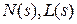- многочлены с единичными коэффициентами при младших членах.

2. Передаточная функция замкнутой системы по 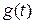при ( ).

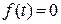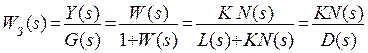, где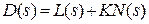

3. Передаточная функция замкнутой системы по ошибке 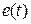по задающему воздействию при ( ).

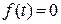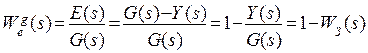
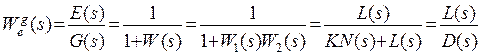
Передаточная функция прямой цепи по возмущению 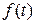при ( )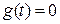

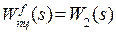
4. Передаточная функция разомкнутой системы по возмущению 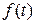при ( )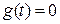

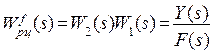
5. Передаточная функция замкнутой системы по возмущению 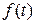при ( )

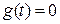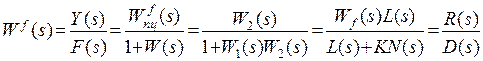, где 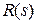- многочлен зависит от места приложения возмущающего воздействия.

6. Передаточная функция замкнутой системы по ошибке 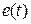по возмущению при ( ).

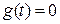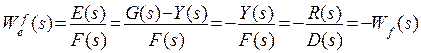
Для замкнутой системы изображение выходного сигнала имеет вид:

.

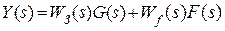
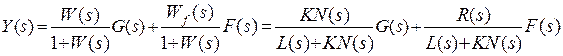Приближённое исследование точности системы в установившемся режиме

Определение установившейся ошибки может быть произведено разными способами.

Первый способ, наиболее простой, позволяет оценить ошибку системы без сложных вычислений. Он основан на использовании передаточных функций системы по ошибке и теоремы о конечном значении функции.

Пусть задана передаточная функция разомкнутой системы в виде 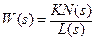. На вход системы поступают задающее воздействие 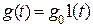и возмущение f(t). Для определения ошибки в замкнутой системе необходимо найти передаточную функцию по ошибке для соответствующего воздействия:

.

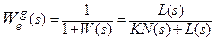
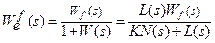Определим точность системы при отработке задающего воздействия, для чего используем теорему о конечном значении, т.е. .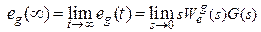

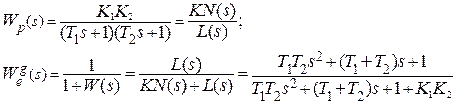
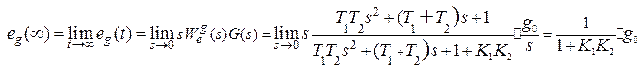
Второй способ применяется для случая детерминированных медленно меняющихся воздействий.

Разложим передаточную функцию замкнутой системы по ошибке по возрастающим степеням комплексной переменной в ряд, сходящийся при малых s

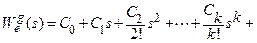
Изображение ошибки будет иметь вид:

.

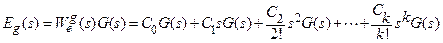Если передаточная функция является дробно-рациональной, то разложение в ряд можно осуществить простым делением числителя на знаменатель, располагая члены полиномов в порядке возрастания степеней.

Если воздействие дифференцируемо на всем интервале от 0 до 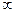, то ошибка системы может быть представлена в виде ряда

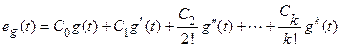или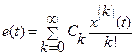

Коэффициенты 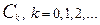называются коэффициентами ошибок системы.

Коэффициенты ошибок могут быть также определены по формулам разложения передаточной функции по ошибке в ряд Тейлора:

.

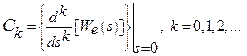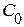- коэффициент статической или позиционной ошибки, 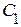– коэффициент скоростной ошибки, 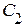– коэффициент ошибки от ускорения.

В статических системах все коэффициенты ошибок не равны нулю.

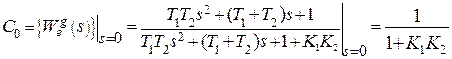
В системах с астатизмом 1 порядка – .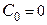

.

.

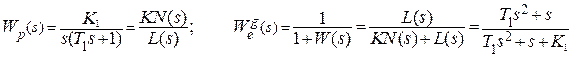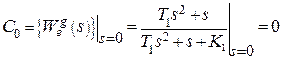Коэффициенты ошибок позволяют определить как будет изменяться ошибка системы при подаче на вход различных видов воздействий, а также зависимость установившейся ошибки от структуры системы и ее параметров.

Практическая часть.

Для заданной системы провести анализ качества процессов управления, если

.

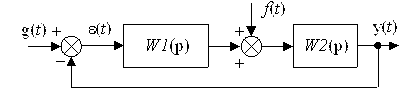
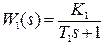
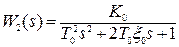
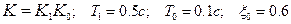С учётом заданных параметров передаточная функция прямой цепи:

.

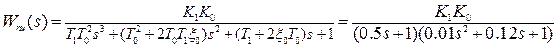Передаточная функция замкнутой системы .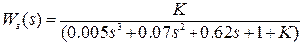

Рассмотрим вариант, если .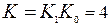

Поведем анализ качества заданной системы.

1. Анализ устойчивости.

1.1. необходимое условие устойчивости.

Рассмотрим характеристический полином замкнутой системы

.

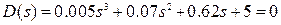Коэффициенты характеристического полинома вещественные и положительные, необходимое условие устойчивости выполняется.

1.2. оценка устойчивости по кривой переходного процесса.

Привести график переходной характеристики из домашнего задания № 1.

Определим конечное значение переходной функции (вычисляется только для устойчивых систем).

Если система устойчива, то переходная функция системы должна стремиться к установившемуся значению, т.е

.

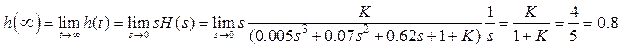h(t)=0.8-0.407exp(-10.994t)-0.393exp(-1.5028t)Сos9.4179t-0.5378exp(-1.5028t) Sin9.4179t.

1.3. оценка устойчивости по корням характеристического уравнения.

Корни характеристического уравнения .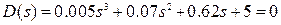

; ; .

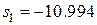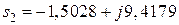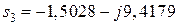Действительные части корней являются отрицательными, следовательно, корни располагаются в левой полуплоскости и заданная система устойчива.

1.4. по критерию устойчивости Гурвица.

Составим определители Гурвица для системы третьего порядка. Номер определителя определяется номером коэффициента, для которого составляется определитель.

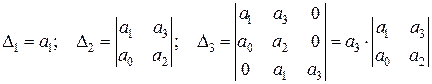
Критерий Гурвица. Для того чтобы система была устойчива, необходимо и достаточно, чтобы все определители данной системы были положительными при 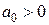, т.е. .

.

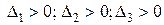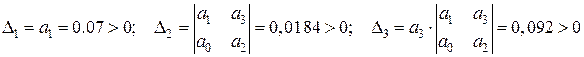Условие устойчивости для системы третьего порядка: .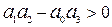

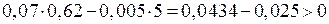. – система устойчива.

Определим значение критического коэффициента устойчивости:

.

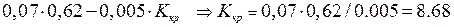1.5. по критерию устойчивости Михайлова.

Рассмотрим характеристический полином замкнутой системы

.

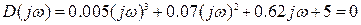Выделим действительную 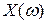и мнимую 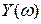части полинома :

;

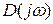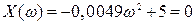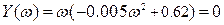
Построим кривую Михайлова.

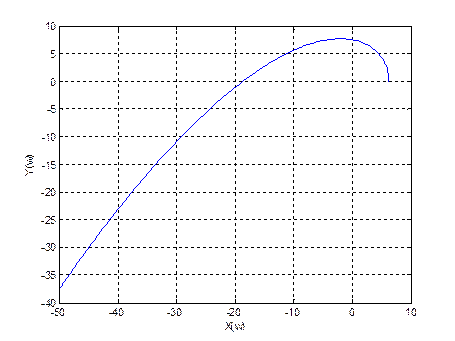
Рис. 8. График кривой Михайлова

(При построении кривой Михайлова брать диапазон частот чуть больший, чем последняя частота )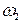

Кривая Михайлова, начинаясь на вещественной положительной полуоси, огибает начало координат в направлении против часовой стрелки и проходит последовательно три квадранта, следовательно, система устойчива.

Проверим устойчивость по правилу чередования частот:

Определим точки пересечения с вещественной и мнимой осями

.

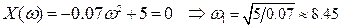
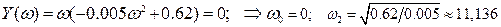
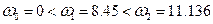Система устойчива, т.к. выполняется условие чередования частот.

1.6. по критерию устойчивости Найквиста.

Оценка устойчивости проводится по АФЧХ разомкнутой системы.

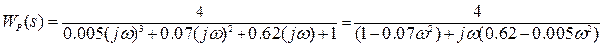
Для построения характеристики выделим действительную и мнимую частотные характеристики

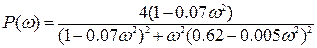
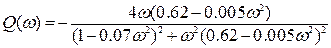
На полученном графике необходимо отметить критическую точку (-1, j0), начало функции при 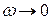, число правых корней .

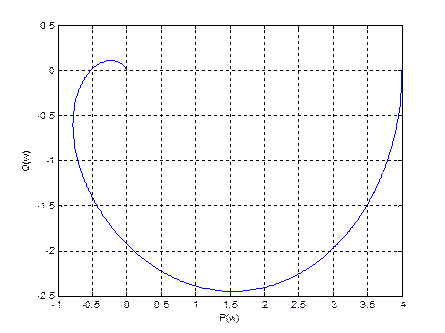
Рис.9 АФЧХ разомкнутой системы.

Замечание. Если АФЧХ разомкнутой системы начинается в бесконечности, то при построении характеристики интервал частот надо выбирать не с нуля.

По графику АФЧХ разомкнутой системы можно сделать заключение: годограф 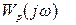при изменении частоты не охватывает критическую точку (-1, j0), т.к. система в разомкнутом состоянии устойчива, то замкнутая система устойчива.

Проверим правильность построения функции по контрольным точкам пересечения с осями: .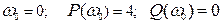

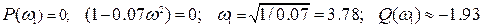
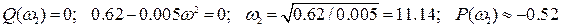
Точка пересечения годографа с вещественной осью равна -0.52, что меньше единицы. Полученные расчётные данные совпадают с графическими.

2. Анализ качества переходного процесса

2.1. Построение переходной характеристики замкнутой системы 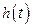и определение по ней прямых показателей качества.

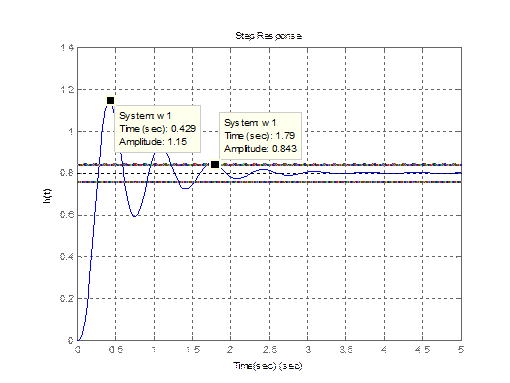
Рис. 10. Переходная функция замкнутой системы.

Для определения по кривой переходного процесса времени управления на графике строятся линии, соответствующие значениям 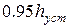и 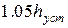. Время, по истечении которого кривая переходного процесса входит в 5% трубку, является временем управления .

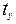1. По графику время управления ;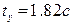

Для определения по кривой переходного процесса перерегулирования системы необходимо на графике определить установившееся значение и максимальное значение функции и рассчитать перерегулирование по формуле.

2.

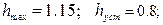
Перерегулирование: ;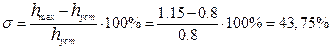

3. Период колебаний по кривой переходного процесса - .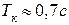

4. Частота колебаний - .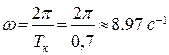

5. Время нарастания - .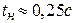

6. Время достижения первого максимума - .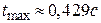

7. Число колебаний: n=3;

2.2 Корневые показатели качества:

Корни: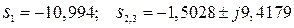

Степень устойчивости: .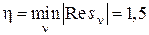

Степень устойчивости позволяет оценить инерционные свойства системы, т.е. время переходного процесса

.

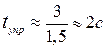Степень колебательности: ; .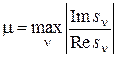

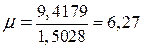Степень колебательности позволяет оценить колебательные свойства системы, т.е. перерегулирование

.

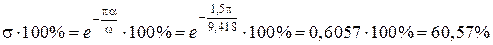Период колебаний - 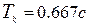, число колебаний - .

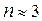2.2. Анализ заданной системы с использованием частотных показателей качества, для этого

· построить график амплитудно-частотной характеристики замкнутой системы 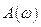. По графику определить частотные показатели качества (см. лабораторную работу, эксперимент 2);

· оценить быстродействие и колебательные свойства системы по частотным показателям качества;

· построить график логарифмической амплитудно-частотной характеристики ЛАЧХ разомкнутой системы по выходному сигналу, логарифмической фазочастотной характеристики ЛФЧХ.

Определить время управления и колебательность замкнутой системы, запасы устойчивости по фазе и амплитуде.

Частотные показатели определяются по амплитудно-частотной характеристике замкнутой системы.

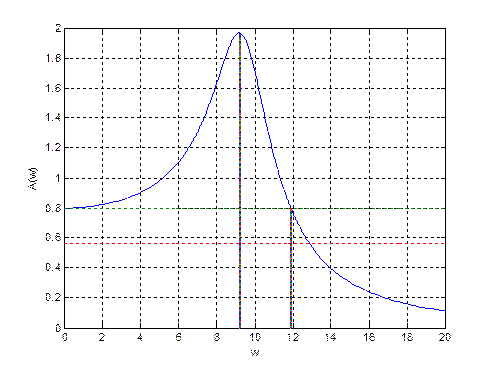
Амплитудно-частотная характеристика замкнутой системы

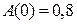– начальное значение амплитудной характеристики;

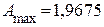– максимальное значение амплитудной характеристики;

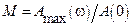=2,4594 – показатель колебательности;

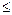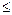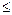Показатель колебательности М характеризует склонность системы к колебаниям. При М 1 переходный процесс не колебательный, при 1,1 М 1,5 переходный процесс соответствует хорошо демпфированной системе ( 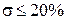), при М 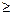1,5 переходный процесс имеет ярко выраженный колебательный характер ( ).

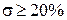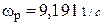- резонансная частота;

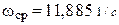- частота среза;

Полоса пропускания системы от 0 до .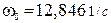

Определение динамических свойств системы:

Инерционные свойства системы можно оценить по частоте среза, выбор числа колебаний за время переходного периода определяется величиной показателя колебательности 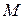. Чем больше показатель, тем выше колебательные свойства системы, поэтому в данном случае можно взять число колебаний в пределах от 3 до 4.

·

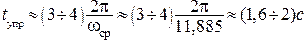
Величина показателя колебательности предполагает перерегулирование в пределах 50-60%.

Оценка точности в установившемся режиме: 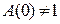, это свидетельствует о том, что коэффициенты передаточной функци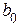и и 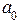не равны, ошибка системы по задающему воздействию равна .

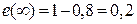Определение запасов устойчивости по фазе 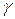и амплитуде 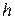можно провести по логарифмическим амплитудно-частотной и фазочастотным характеристикам.

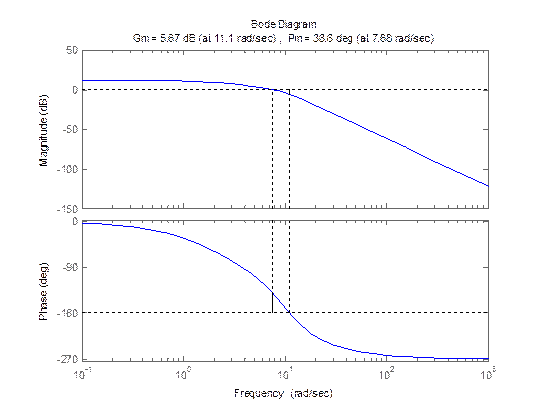
ЛАЧХ и ЛФЧХ разомкнутой системы

3. Анализ точности в установившемся режиме при отработке воздействий

Для анализа точности системы необходимо определить передаточные функции системы по воздействиям, приходящим на систему. Количественно точность определяется величиной ошибки.

Определим по правилам быстрого вычисления (стр.13-14 ) передаточную функцию заданной системы по ошибке по входному воздействию. Для этого воспользуемся передаточной функцией разомкнутой системы

Точность системы в установившемся режиме при отработке типовых воздействий определяется величиной ошибки по соответствующему воздействию. Для вычисления ошибки необходимо определить передаточные функции по ошибке и числовые показатели качества в установившемся режиме – коэффициенты ошибок. Для заданной системы определим передаточные функции по ошибке по входному воздействию и возмущению с учётом формул быстрого вычисления.

.

.

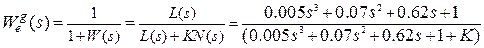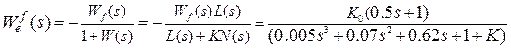Определим коэффициенты 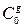и :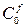

;

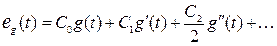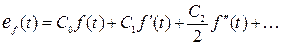
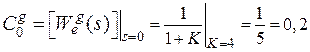
Вычисление коэффициентов ошибок путём деления полинома числителя на полином знаменателя.

Коэффициенты ошибок передаточной функции замкнутой системы по ошибке по задающему воздействию.

; ;

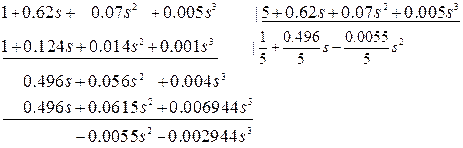
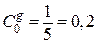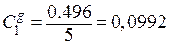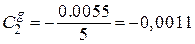
Коэффициенты ошибок передаточной функции замкнутой системы по ошибке по возмущению.

; ; .

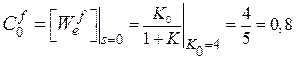
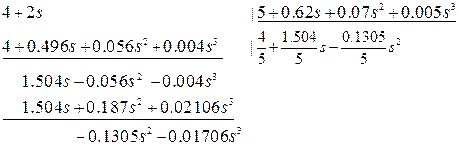
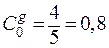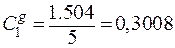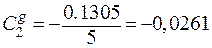Графики функци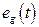й и 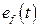, построенные с использованием стандартной функции пакета Matlab «step».

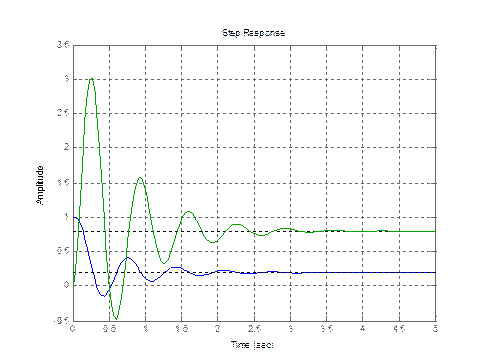
Определить величину ошибки системы при заданных преподавателем входных сигналах.

Для выполнении этого пункта необходимо получить индивидуальное задание у преподавателя, определяющего место приложения возмущения и вид функций.

Приложение.

1. Анализ устойчивости:

П остроение кривой Михайлова:

>> w=[0:0.01:30];

>>s=i.*w;

>> D=0.005.*s.^3+0.07.*s.^2+0.62.*s+5;

>> DR=real(D); DI=imag(D);

>> plot(DR,DI);grid on;xlabel('X(w)'),ylabel('Y(w)')

Построение годографа разомкнутой системы:

>>w=[0:0.001:500];

>> W=4./(0.005.*s.^3+0.07.*s.^2+0.62.*s+1);

>> WR=real(W);WI=imag(W);

>> plot(WR,WI);grid on;xlabel('P(w)'),ylabel('Q(w)')

2. Построение переходной функции и определение по ней прямых показателей качества

2.1 Построение переходной функции с использованием стандартной функции «step» и 5-ти % трубки:

>>K=4;p=[0.005 0.07 0.62 1+K];q=[K];

>> w1=tf(q,p);

>> step(w1,5); grid on;xlabel('Time(sec)'), ylabel('h(t)') % построение переходной функции

>> hold on % сохранение текущего графика на экране

>> hyct=K./(1+K) % задание установившегося значения

hyct = 0.8000

>> delta=0.05;d=delta.*hyct;

d = 0.0400

>> h1=hyct-d % нижняя граница 5-ти % трубки:

h1 = 0.7600

>> h2=hyct+d % верхняя граница 5-ти % трубки

h2 = 0.8400

>> t=[0:0.01:5];

>> plot(t,h,t,h1,':',t,h2,':');grid on; xlabel('Time(sec)'), ylabel('h(t)') % построение линий на графике.

2.2 Вычисление 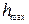переходной характеристики и перерегулирования:

(использовать переходную функцию, полученную в домашнем задании № 1)

>>h=0.8-0.407.*exp(-10.994.*t)-0.393.*exp(-1.5028.*t).*Сos(9.4179.*t)-0.5378.*exp(-1.5028.*t).*

Sin(9.4179.*t).

>>hmax=max(h)

hmax = 1.1475

>>sigma1=100.*(hmax - hyct)/ hyct % перерегулирование, рассчитанное по h(t)

sigma1 = 43.4375

2.3. Вычисление показателей качества переходного процесса по корням:

>>mu=9.4179/1.5028 % степень колебательности

mu = 6.2669

>> sigma2=100.*exp(-pi/mu) % перерегулирование, рассчитанное по корням

sigma2 = 60.5743

>> Tk=2*pi/9.4179

Tk = 0.6672 % период колебаний

>> tp=3/1.5028

tp = 1.9963 % время управления

>> n=tp/Tk

n = 2.9922 % число колебаний

2.4.Определение показателей качества по АЧХ замкнутой системы

>> K=4;p=[0.005 0.07 0.62 1+K];q=[K];

>>bode(q,p); grid on

Для снятия значений частот при получении характеристики правой кнопкой мыши открыть свойства функции и изменить настройки, а именно, в «units» установить вместо логарифмической шкалы установить скалярную, а шкалу измерения амплитуды с dB на absolute. При установке курсора на какую-либо точку графика будет указываться значение амплитуды и частоты.

2.5. Определение запасов устойчивости по амплитуде и фазе по ЛАЧХ и ЛФЧХ разомкнутой системы

>> K=4;p=[0.005 0.07 0.62 1];q=[K];

>> sys=tf(q,p); % передаточная функция разомкнутой системы

>> [Gm,Pm,Wq,Wp]=margin(sys) -

Gm = 1.9207 % запас устойчивости по амплитуде

Pm = 38.6416 % запас устойчивости по фазе в градусах

Wq = 11.1374 % частота измерения запаса устойчивости по амплитуде ( )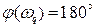

Wp = 7.6758 % частота среза ( )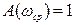

>>Gm_dB=20*log10(Gm)

Gm_dB = 5.6693 % запас устойчивости по амплитуде в децибелах

>> margin(sys) % построение ЛАЧХ и ЛФЧХ разомкнутой системы

3. Построение функций 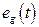и с использованием стандартной функции пакета Matlab «step».

>>qe=[0.005 0.07 0.62 1];p=[0.005 0.07 0.62 1+K];

>> syseg=tf(qe,p); % передаточная функция замкнутой системы по ошибке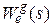

>> step(syseg,5); grid on

>> qf=[2 4];p=[0.005 0.07 0.62 5];

>> sysef=tf(qf,p); % передаточная функция замкнутой системы по ошибке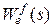

>> hold on

>> step(sysef,5)