Оценка плотности вероятностей и функции распределения

Построение эмпирических распределений.

Просматривая результаты наблюдений (измерений) трудно заметить какую-либо закономерность в их изменении. Выявить такие закономерности позволяют статистические методы.

Предварительная статистическая обработка опытных данных начинается обычно с того, что их располагают в порядке возрастания (точнее, неубывания). Упорядоченная таким образом выборка называется вариационным рядом, а сама процедура упорядочения – ранжированием (или сортировкой) опытных данных.

Наглядной формой графического представления эмпирических данных является гистограмма, полигон, эмпирическая функция распределения и полигон накопленных частот. При этом гистограмма и полигон относительных частот аппроксимируют неизвестную плотность распределения, а эмпирическая функция распределения и полигон накопленных относительных частот – интегральную функцию распределения генеральной совокупности. Построение гистограммы (полигона) позволяет обоснованно выдвигать гипотезы о законе распределения обрабатываемых экспериментальных данных. Зная закон распределения наблюдаемой случайной величины можно решать многие практические задачи, связанные с обработкой результатов измерений, контролем качества продукции, оценкой эффективности и стабильности технологических процессов.

При непрерывном распределении случайной величины 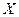эмпирическая плотность распределения вероятностей может быть изображена в виде гистограммы или полигона относительных частот. Для этого должна быть выполнена группировка значений выборки, которая состоит в следующем.

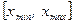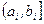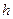Весь интервал , в котором заключены элементы выборки, разбивается на ряд частичных непересекающихся интервалов (разрядов) длины и подсчитывается число элементов выборки 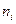, попавших в 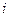-й интервал 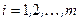. Параллельно вычисляется и относительная частота 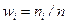. При графическом изображении гистограммы и полигона каждый интервал удобнее представлять не двумя границам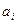и и 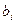, а одним значением 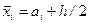- серединой интервала.

Гистограммой частот называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длины 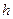, а высоты равны отношению 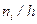(плотность частоты). Площадь частичного 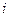-го прямоугольника равна 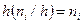- числу выборочных элементов, попавших в 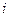-й интервал. Площадь гистограммы частот равна объему выборки .

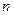Полигон частот – это ломаная линия, получающаяся при соединении точек с координатами 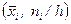, т.е. соединяются середины верхних сторон прямоугольников гистограммы.

Аналогично определяется гистограмма и полигон относительных частот.

Для гистограммы относительных частот площадь частичного 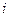-го прямоугольника равна 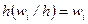-относительной частоте элементов, попавших в 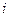-й интервал. Площадь гистограммы относительных частот равна сумме всех относительных частот, т. е. единице. При достаточно большом объеме выборки высоты построенных прямоугольников дают приближенные значения плотности распределения 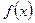в средних точках 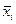интервалов 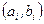. Гистограмма – кусочно-постоянная аппроксимация (неизвестной) плотности распределения генеральной совокупности.

Полигон относительных частот – это ломаная линия, соединяющая точки 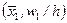, ,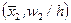…, , 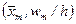где 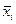- середины интервалов группирования, 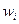- соответствующие им относительные частоты. Полигон – кусочно-линейная аппроксимация плотности распределения генеральной совокупности.

Наглядное представление об интегральной функции распределения дают эмпирическая функция распределения и полигон накопленных относительных частот.

Эмпирической (выборочной) функцией распределения называется функция 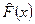, определяющая для каждого значения 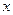относительную частоту события 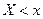. Строится она так. Для данного числа 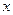подсчитывается число элементов вариационного ряда 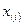, меньших 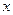и делится на объем выборки:

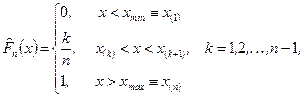
Используя функцию единичного скачка

,

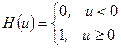формулу для эмпирической функции распределения можно записать более компактно

.

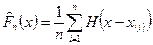Полигон накопленных частот – это график ломаной линии, соединяющей точки

, , … , , … , ,

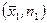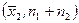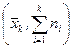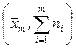c абсциссами, равными правым границам интервалов группирования, и ординатами, равными накопленным частотам.

Аналогично, полигон накопленных относительных частот – это ломаная линия, получающаяся соединением точек с координатами

, , … , , … , .

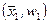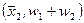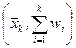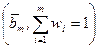В математической статистике доказывается, что гистограмма и полигон относительных частот являются состоятельными оценками плотности распределения, а полигон накопленных относительных частот (или эмпирическая функция распределения) – состоятельной оценкой истинной функции распределения генеральной совокупности. При этом, чем больше объем выборки, тем мельче можно взять интервалы разбиения 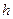и тем точнее гистограмма и эмпирическая функция распределения будут аппроксимировать соответствующие теоретические распределения.

Число интервалов группирования эмпирических данных 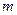существенно влияет на вид гистограммы. Четких рекомендаций на этот счет не существует, ясно лишь то, что это число не должно быть «очень малым» или «очень большим». Для выборок среднего объема (несколько сотен элементов) число интервалов обычно выбирают в диапазоне 8 – 12. Согласно рекомендации ВНИИ Метрологии им. Д.И. Менделеева в зависимости от объема выборки 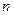число интервалов группирования 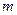следует выбирать согласно таблице

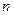	40 – 100	100 – 500	500 – 1000	1000 – 10000
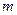	7 – 9	8 – 12	10 – 16	12 – 22

Часто в литературе по математической статистике для выбора оптимального значения 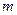рекомендуется формула

,

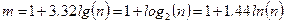записанная с использованием десятичного, двоичного или натурального логарифма; или формула

,

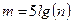где 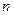- объем выборки. Существуют и иные рекомендации. Однако все рекомендуемые формулы не имеют строгого обоснования и дают лишь ориентировочное количество интервалов 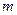, которое при желании может быть изменено в ту или другую сторону.

При определении диапазона возможных значений параметра 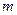можно ориентироваться на формулы

, ,

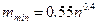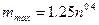дающие оценки минимального и максимального значения данного параметра. В качестве оптимального значения 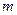рекомендуется выбирать целое число из интервала 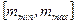. Обычно в этот интервал попадает несколько целых чисел; после построения гистограмм для каждого из этих чисел, «оптимальное» значение параметра 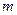определяется визуально. Для симметричных распределений в качестве значения 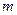рекомендуется выбирать нечетное целое число из интервала .

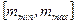После определения 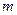вычисляется длина интервалов группирования

,

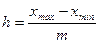и производятся все дальнейшие вычисления, необходимые для построения гистограммы, полигона и эмпирической функции распределения.

Доверительная область для функции распределения, соответствующая уровню доверия 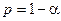, определяется неравенствами

.

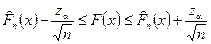Эти неравенства выполняются сразу для всех значений 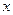с вероятностью, близкой к 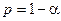. Данный результат следует из теоремы Колмогорова А.Н., доказываемой в курсе теории вероятностей. Здесь 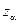- корень уравнения (квантиль функции распределения Колмогорова)

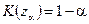, (1)

а 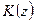- функция (распределения) Колмогорова, определяемая абсолютно сходящимся функциональным рядом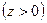

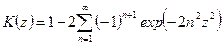. (2)

Этот ряд сходится крайне неравномерно, поэтому для достижения одной и той же точности при различных значениях 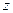приходится сохранять различное количество членов ряда (2). Оценки показывают следующее. Чтобы обеспечить точность вычисления функции 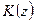порядка 10^-6 в окрестности точки 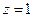достаточно сохранить три члена ряда, при 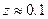уже около 30 членов, а при 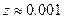около 2700 членов ряда. Таким образом, когда 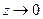, количество членов ряда растет пропорционально 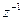. Но поскольку нас интересует только решение уравнения (1) при малых значениях 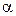, когда 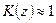и 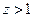, функцию (2) для наших целей можно записать в виде

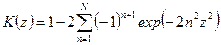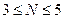, , (3)

сохранив в сумме всего три – пять слагаемых.

Когда вероятность 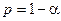близка к единице, квантиль функции распределения Колмогорова можно определить, не решая уравнение 1, по следующей приближенной формуле:

.
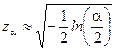