Согласование результатов испытаний на различных этапах ЭО
Подход, рассмотренный выше, предполагал, что в процессе проведения испытаний используется статистическая информация о времени работы системы до отказа, оцениваемая на различных этапах ЭО с различным уровнем достоверности. В то же время при проведении ЭО могут встретится ситуации, когда измерения действующих и допустимых значений параметров происходит на различных этапах испытаний, в частности, на этапе стендовой отработки оцениваются допустимые параметры работоспособности системы, а на завершающем этапе испытаний измеряются действующие значения параметров. В этом случае стендовые испытания дают представление о ресурсах конкретных систем. Например, проводятся разрушающие испытания отсеков конструкции изделия, граничные испытания элементов системы управления на определение областей работоспособности систем и др. При этом случайный характер внешних воздействий может быть учтен только на завершающем этапе испытаний.
В дальнейшем допустим, что работоспособность системы определяется параметром 
. Причем на этапе стендовых испытаний оцениваются допустимые значения параметров 
, а на завершающем этапе испытаний – действующие значения 
. По результатам испытаний можно получить точечные оценки математических ожиданий этих параметров 
и 
. Соответственно точечная оценка коэффициента запаса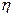 
будет равна
.
В дальнейшем предположим, что работоспособность устройства обеспечивается при выполнении неравенства 
. Тогда, в случае нормального закона распределения параметра 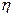, нижняя граница надежности 
, подтверждаемая при завершении ЭО, может быть оценена по соотношению
,
где 
; 
нижняя граница одностороннего доверительного интервала оценки математического ожидания коэффициента запаса ;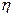 
коэффициенты вариации соответственно допустимых и действующих значений параметров;
число испытаний соответственно при проведении измерений допустимых и действующих значений параметров ; 
принятый уровень доверительной вероятности ; 
.
При планировании количества испытаний на различных этапах ЭО воспользуемся оценкой прогнозируемого уровня математического ожидания коэффициента запаса, потребного для обеспечения заданных требований 
к надежности устройства
, (2.55 )
где 
.
Как видно из соотношения ( 2.55 ) заданный уровень надежности может быть обеспечен при различных комбинациях значений коэффициента запаса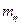 
и количества испытаний 
и 
. Очевидно эти параметры целесообразно задавать такими, чтобы соотношение ( 2.20 ) выполнялось при минимальных затратах средств. В общем случае суммарные затраты на реализацию целевой программы можно представить в виде
, ( 2.56 )
где 
стоимости проведения одного испытания соответственно при проведении стендовых и завершающих испытаний ; 
затраты на производство и эксплуатацию изделия при выполнении целевой программы; 
функция потерь при отказах; 
ущерб при отказе системы на завершающем этапе испытаний; 
среднее число отказов на завершающем этапе испытаний.
Очевидно стоимость 
будет зависеть от уровня избыточности системы по определяющему параметру 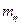, величина которого закладывается на этапе проектной разработки. При заданном уровне 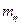дисциплинирующее условие ( 2.55 ) можно представить в виде
В рассматриваемом случае функция Лагранжа будет равна
Таким образом оптимальные значения искомых параметров будут удовлетворять системе алгебраических уравнений
Раскрывая выражения для производных, получим
После преобразований, получим
, ( 2 57 )
где 
Таким образом оптимальное соотношение объемов испытаний на различных этапах ЭО не зависит от требований, предъявляемых к надежности
устройства , а так же не зависит от уровня его параметрической избыточности 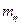. С учетом соотношения ( 2.57 ) суммарные затраты будут равны
,
где 
.
Дисциплинирующее условие ( 2.55 ) в дальнейшем представим в виде
,
где 
.
Подставляя выражение для из соотношения ( 2.57 ), получим
, ( 2.58 )
где 
При оптимизации объема испытаний воспользуемся выражением для эксплуатационных затрат
, где 
.
В рассматриваемом случае условие оптимальности примет вид 
.
Раскрывая выражение для производной, получим
.
Разрешая уравнение относительно , найдем оптимальный объем стендовых испытаний
. ( 2.59 )
Знание позволяет оценить параметр 
и соответствующий ему уровень избыточности системы
, где 
.
При проведении расчетов первого приближения значения производных 
принимаются равными нулю. В этом случае можно принять 
.
В дальнейшем по соотношениям ( 2.57 – 2.59 ) оцениваются оптимальные значения параметров 
первого приближения. В окрестности полученного квазиоптимального решения рассчитываются значения функции 
,
где 
вероятнть отказа при проведении первого испытания на завершающем этапе отработки; 
.
Оценка производных 
могут быть получены численно либо графически.
В дальнейшем проводится итерационное уточнение квазиоптимального решения с учетом полученных значений производных.
Пример. Для иллюстрации предлагаемого подхода рассмотрим модельный пример. При проведении расчетов примем следующие исходные данные : 
При расчете первого приближения были получены следующие результаты:
Зависимость функции потерь при отказах 
от числа испытаний 
рассчитывалась по соотношению
, где 
.
Результаты расчетов представлены на графиках ( рис. 2.20 и рис. 2 21 ).
Рис. 2.20 Зависимость функции потерь от числа испытаний
для различных значений .
Рис. 2 21 Зависимость функции потерь от числа испытаний
для различных значений .
С помощью графиков искомые производные оценивались в окрестности квазиоптимального решения по приближенным соотношениям
Отсюда
Соответственно для остальных параметров получим
Таким образом окончательно можно принять: 