Основные кинематические характеристики механизмов
ЛЕКЦИЯ № 3
Анализ и синтез рычажных механизмов
Структурный анализ
По классификации Л.В.Ассура* - И.И.Артоболевского стойка и звено, образующие одноподвижную кинематическую пару Р1 – вращательную или поступательную, условно называют начальным механизмом 1 класса (рисунок 2.1).
Рисунок 2.1а – первая модификация – I1
Рисунок 2.1б – вторая модификация – I2
К I классу относятся простейшие механизмы электродвигатели, вентиляторы.
Степень подвижности: W = 3n-2Р1-Р2 = 3х1 – 2х1 – 0 = 1.
| а) |
| б) |
| О |
| О1 |
| О |
| О |
Рисунок 2.1
Более сложный механизм образуется присоединением к механизму I класса структурных групп с нулевой степенью подвижности, которые называются группы Ассура, т.е. W = 3n-2Р1 = 0.
Откуда 3n = 2Р1 и Р1 = (3/2)n.
Так как число кинематических пар не может быть дробным, то число звеньев групп Ассура должно быть четным, тогда число кинематических пар будет кратно 3 (таблица 2.1)
Таблица 2.1
| n | … | |||
| Р1 | … |
Первое сочетание чисел n = 2, Р1 = 3. Группа, имеющая 2 звена и 3 одноподвижные кинематические пары – Р1, называется группой II класса, второго порядка или двухповодковой группой (диада), т.к. присоединение этой группы к другим группам (или стойкам) производится двумя поводками. Если все 3 кинематические пары вращательные, то двухповодковая группа будет первой модификации (рисунок 2.2а).
| а) II класс 2 порядок 1 вид |
| б) II класс 2 порядок 2 вид |
| в) II класс 2 порядок 3 вид |
| г) II класс 2 порядок 4 вид |
| д) II класс 2 порядок 5 вид |
| ВПП |
| ПВП |
| ВВВ |
| ВВП |
| ВПВ |
Рисунок 2.2 -Группы Ассура 2-го класса
Все последующие модификации получены путем замены отдельных вращательных пар поступательными (рисунки 2.2б-д).
Степень подвижности: W = 3n-2Р1 = 3х2 – 2х3 = 0.
Присоединение диады 1-й модификации к начальному механизму I класса образует шарнирный четырехзвенник (кривошипно-коромысловый механизм) (рисунок 2.3 а).
Присоединение диады 2 модификации к механизму I кл. образует кривошипно-ползунный механизм (рисунок 2.3 б).
Диады остальных модификаций с тем или иным начальным звеном образуют кулисные механизмы (рисунок 2.3 в,г).
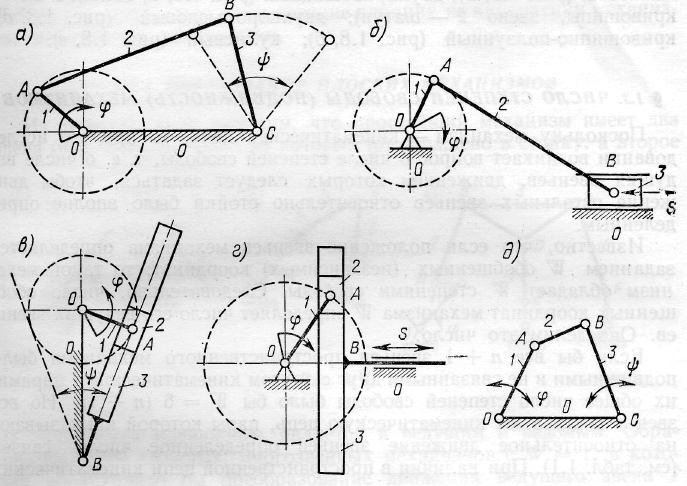
Рисунок 2.3
Следующее сочетание n = 4, Р1 = 6. Незамкнутая цепь из 4-х звеньев и шести одноподвижных кинематических пар – Р1, является группой III класса, 3 порядка или трехповодковой группой (триада) (рисунок 2.4).
Степень подвижности: W = 3n-2Р1 = 3х4 – 2х6 = 0.
Рисунок 2.4 -Группа Ассура 3-го класса
Отличительным признаком является треугольное звено 2, которое называется базисным. Различные модификации этих групп можно получить, если вращательные пары сочетать с поступательными.
Структурные группы более высоких классов в существующих механизмах находят весьма ограниченное применение.
Итак, структурные группы с W = 0 (группы Ассура) подразделяется на классы и порядки. Класс группы (с n > 2 и Р1 > 3) равен числу кинематических пар, входящих в наиболее сложный замкнутый контур.
Порядок группы равен числу внешних, свободных кинематических пар, с помощью которых группу можно присоединить к другим звеньям.
Если в состав механизма входят группы различных классов, то класс механизма определяется наивысшим классом входящей в него группы.
Структурный анализзаключается в разложении механизма на структурные группы и начальные звенья.
Цель: определить число и название звеньев, число и класс кинематических пар, степень подвижности, класс и порядок структурных групп, класс механизма в целом, формулу строения (порядок сборки).
Основой служит структурная схема механизма.
При проведении структурного анализа рекомендуется:
- отсоединять структурные группы начинать с наиболее удаленных от ведущего звена;
- отделять наиболее простые группы II кл. (диады – 2 звена и 3 кинематические пары);
- следить за тем, чтобы степень подвижности механизма до и после отделения каждой структурной группы оставалась неизменной;
- помнить, что каждое звено и каждая кинематическая пара может входить только в одну структурную группу.
Например, от шестизвенного механизма (рисунок 2.5а), имеющего одну степень подвижности (W = 3n-2Р1 = 3х5 – 2х7 = 1), отделяем наиболее удаленную от входного звена структурную группу Ассура II класса, состоящую из звеньев 4 и 5 и трех кинематических пар О3, Д, С (рисунок 2.5в). Степень подвижности этой группы W = 3n-2Р1 = 3х2 – 2х3 = 0. Это группа II кл. 2 пор. 2 мод. (II2 (4-5).
Степень подвижности оставшегося 4-х звенного механизма не изменилась
W = 3n-2Р1 = 3х3 – 2х4 = 1 (рисунок 2.5б).
Отсоединим следующую группу звеньев 2-3 и кинематические пары О₂, В, А (рисунок 2.5д). Это группа II кл. 2 пор. 1 мод. (II1(2-3).
W = 3n-2Р1 = 3х2 – 2х3 = 0
Остается входное звено, шарнирно соединенное со стойкой, являющееся механизмом I класса I вида W = 3n-2Р1 = 3х1 – 2х1 = 1 (рисунок 2.5г).
Класс механизма в целом – II. Формула строения (порядок сборки).
I1(1) ® II1(2-3) ® II2(4-5).
Класс, порядок и вид групп Ассура и механизма в целом зависит не только от самого механизма, но и от того, какое звено является ведущим.
Если в плоском механизме имеются высшие кинематические пары, то их следует заменять низшими. При замене высших пар низшими должно быть соблюдено условие структурной эквивалентности – число условий связи заменяющей кинематической цепи должно равняться числу связей заменяемой высшей пары. С этой точки зрения каждая высшая пара эквивалентна одному звену, входящему в две низшие пары. Ведомое звено заменяющего механизма должно иметь те же перемещения, скорости и ускорения, что и реальный механизм с высшей кинематической парой. Например, кулачковый механизм (рисунок 2.7а) с высшей парой Р2 может быть заменен кривошипно-ползунным (рисунок 2.7б).
Центры шарниров А и В совпадают с центрами кривизны элементов высшей пары. Высшая пара заменена звеном 2 и двумя низшими парами
А и В.
| W = 3n - 2P1 = 3·1 - 2·1 = 1 |
| W = 1 |
| W = 3n - 2P1 = 3·2 - 2·3 = 0 |
| б) |
| д) |
| г) |
| О2 |
| В |
| А |
| О1 |
| 𝜔1 |
| О1 |
| 𝜔1 |
| = |
| + |
| О2 |
| В |
| А |
| W = 3n - 2P1 = 3·5 - 2·7 = 1 |
| W = 3n - 2P1 = 3·3 - 2·4 = 1 |
| W = 3n - 2P1=3·2 - 2·3 = 0 |
| а) |
| б) |
| А |
| О1 |
| 𝜔1 |
| О3 |
| Д |
| + |
| = |
| С |
| А |
| О1 |
| О2 |
| В |
| 𝜔1 |
| С |
| Д |
| С |
| О2 |
| В |
| в) |
Рисунок 2.4 – Разделение механизма на группы Ассура
| Р2 |
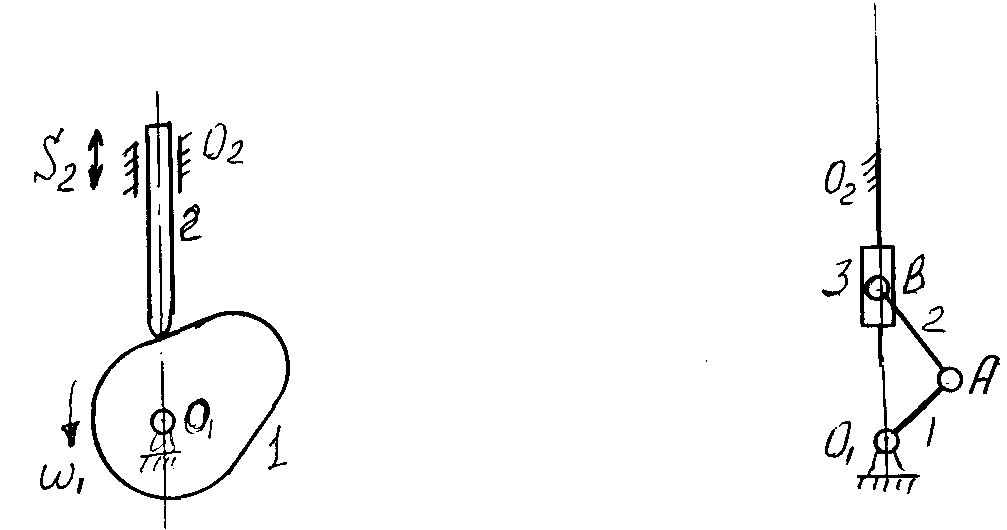
А) б)
Рисунок 2.5
Кинематический анализ
Основные кинематические характеристики механизмов
Движение звеньев любого механизма характеризуется (рисунок 2.6):
а) видом движения:
1) вращательное (кривошип);
2) 
поступательное (ползун в направляющих);
3) плоскопараллельное (шатун);
4) пространственное;
б) перемещением и траекторией;
1) угловые, j рад, - траектория - окружность;
2) линейные, S м,- траектория - линия;
в) скоростью, т.е. быстротой изменения перемещения во времени;
1) угловой,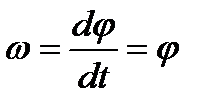 
, рад/с = 1/с = с-1
2) линейной,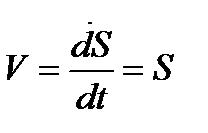 
, м/с;
г) ускорением, т.е. быстротой изменения скорости во времени;
1) угловым,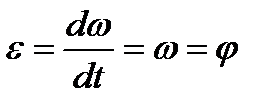 
, рад/с2 = 1/с2 = с-2;
2) линейным,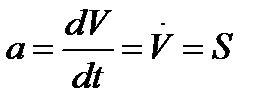 
, м/с2.
Если движение звена 1 принять за абсолютное движение вокруг неподвижной оси 01, то центр вращения будет называться мгновенным центром вращения в абсолютном движении рассматриваемого звена рю (рисунок 2.6).
 |
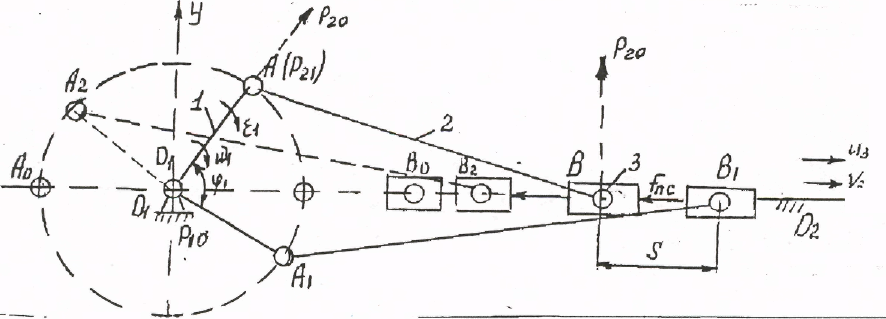Рисунок 2.6
Мгновенный центр вращения звена 2 относительно звена 1 будет в точке Аи будет обозначаться Р21. Геометрическое место мгновенных центров вращения образуют так называемую центроиду. Центроида мгновенного центра вращения Р21 будет представлять собой окружность с радиусом R=l1..
Движение любого механизма может быть периодическим и апериодическим. Периодическое движение характеризуются периодом (циклом), т.е. временем по истечении которого все звенья механизма возвращаются в первоначальное положение. Время цикла Т = 60/n = 2p/w, с, где n - частота вращения кривошипа, об/мин; w - угловая скорость, 1/с.