Використання співвідношень між елементами геометричних фігур
В окремих випадках при доведенні нерівностей можна використовувати певні відомі співвідношення між геометричними фігурами. Мова іде про те, що додатним значенням змінних, що фігурують у нерівності присвоюються деякі кількісні характеристики геометричних фігур (довжини відрізків, площі, об’єми), після чого чисто геометричними методами встановлюються необхідні співвідношення: спочатку між геометричними величинами, а потім роблять відповідні висновки про саму алгебраїчну нерівність.
Задача 4.2.1. Довести, що при довільних додатних чисел 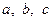 виконується нерівність
виконується нерівність
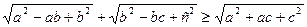 .
.
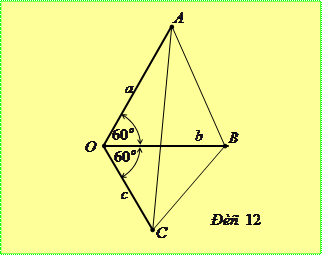
Доведення. Розглянемо відрізки 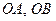 і
і 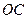 такі, що
такі, що 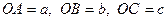 і
і 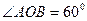 ,
, 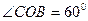 (рис. 12). Маємо
(рис. 12). Маємо 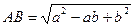 ,
, 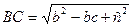 ,
, 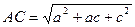 і оскільки
і оскільки 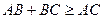 , то нерівність доведено.
, то нерівність доведено.
Задача 4.2.2. При яких значеннях параметра 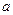 відстань між коренями рівняння
відстань між коренями рівняння
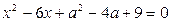
приймає найбільше значення?
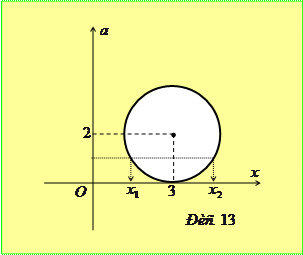 Розв’язання. Перепишемо задане в умові рівняння у виді
Розв’язання. Перепишемо задане в умові рівняння у виді 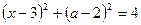 та побудуємо графік одержаної залежності у системі координат
та побудуємо графік одержаної залежності у системі координат 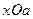 (рис. 13). Очевидно, що при перетині кола прямою
(рис. 13). Очевидно, що при перетині кола прямою 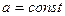 коренями рівняння будуть абсциси точок перетину. Очевидно, що найбільша відстань між коренями рівняння буде дорівнювати діаметру кола, тобто 2 при
коренями рівняння будуть абсциси точок перетину. Очевидно, що найбільша відстань між коренями рівняння буде дорівнювати діаметру кола, тобто 2 при 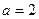 .
.
Задача 4.2.3. Знайти найменше значення виразу
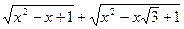 .
.
Розв’язання. Введемо в розгляд функцію
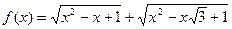 .
.
Насамперед зауважимо, що для всіх 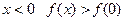 . Тепер зрозуміло, що точку, в якій функція досягає свого найменшого значення, потрібно шукати серед невід’ємних значень змінної.
. Тепер зрозуміло, що точку, в якій функція досягає свого найменшого значення, потрібно шукати серед невід’ємних значень змінної.
Розглянемо випадок, коли 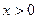 . Тоді можлива наступна геометрична конструкція. Відкладемо два перпендикулярних відрізки
. Тоді можлива наступна геометрична конструкція. Відкладемо два перпендикулярних відрізки 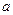 та
та 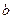 , а також відрізок
, а також відрізок 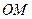 так, що
так, що 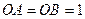 ,
, 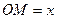 ,
, 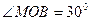 ,
, 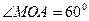 (рис. 14). За теоремою косинусів із трикутників
(рис. 14). За теоремою косинусів із трикутників 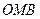 та
та 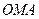 отримуємо
отримуємо
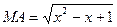 ,
, 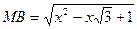 .
.
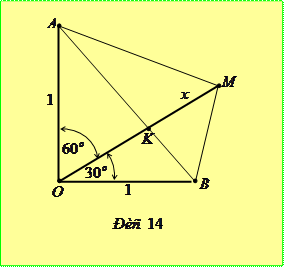 Крім цього бачимо, що
Крім цього бачимо, що 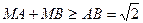 . Рівність досягається тільки у тому випадку, коли точка
. Рівність досягається тільки у тому випадку, коли точка 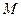 співпадає з точкою
співпадає з точкою 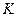 , в якій перетинаються відрізок
, в якій перетинаються відрізок 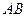 та промінь
та промінь 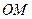 , тобто при
, тобто при 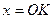 . Довжину відрізка
. Довжину відрізка 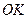 знайдемо із
знайдемо із 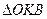 з стороною
з стороною 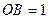 та кутами
та кутами 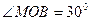 та
та 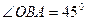 . За теоремою синусів маємо
. За теоремою синусів маємо
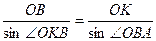 або
або 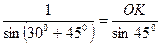 ,
,
звідки 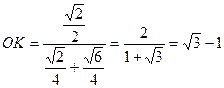 .
.
У випадку 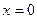 отримуємо
отримуємо 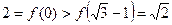 .
.
Отже, найменше значення виразу дорівнює 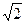 .
.
Задача 4.2.4. Довести нерівність 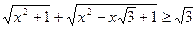 .
.
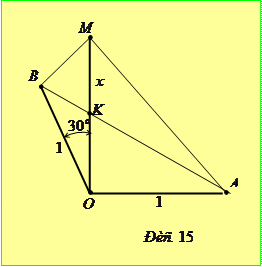 Доведення. Спочатку розглянемо випадок, коли
Доведення. Спочатку розглянемо випадок, коли 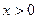 . Тут можлива наступна геометрична конструкція. Відкладемо відрізки
. Тут можлива наступна геометрична конструкція. Відкладемо відрізки 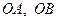 та відрізок
та відрізок 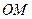 так, що
так, що 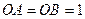 ,
, 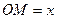 ,
, 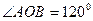 ,
, 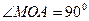 та
та 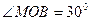 (рис. 15). Тоді
(рис. 15). Тоді 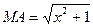 ,
, 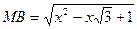 . Тому
. Тому
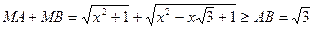 .
.
У випадку, коли 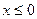 , позначимо
, позначимо 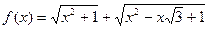 . Тоді для всіх
. Тоді для всіх 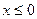 маємо
маємо 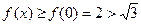 . Тепер можна зробити висновок про те, що задана нерівність виконується при довільних значеннях
. Тепер можна зробити висновок про те, що задана нерівність виконується при довільних значеннях 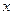 .
.
Задача 4.2.5. Довести, що для довільних значень змінних 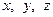 виконується нерівність
виконується нерівність
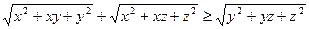 .
.
Доведення. Спочатку розглянемо випадок, коли 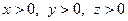 . Відкладемо відрізки
. Відкладемо відрізки 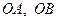 та
та 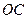 під кутом
під кутом 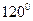 так, щоб
так, щоб 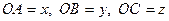 (рис. 16). Зауваживши, що
(рис. 16). Зауваживши, що
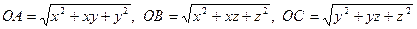
з нерівності трикутника робимо висновок, що задане співвідношення вірне.
Ще дві аналогічні до заданої нерівності отримаємо, зробивши у ній циклічну перестановку змінних 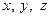 . Мова іде про нерівності
. Мова іде про нерівності
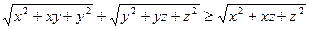 ,
,
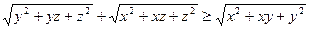 .
.
Розглянемо випадок, коли дві змінні приймають від’ємні, а третя додатне значення (наприклад, 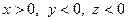 ). Перепозначивши
). Перепозначивши 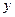 на
на 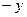 та
та 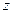 на
на 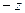 , отримаємо доведену у прикладі 4.2.1 нерівність.
, отримаємо доведену у прикладі 4.2.1 нерівність.
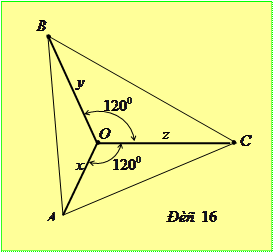 Якщо дві змінні приймають додатні значення, а третя від’ємні (наприклад,
Якщо дві змінні приймають додатні значення, а третя від’ємні (наприклад, 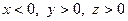 ), то нерівністю у прикладі 4.2.1 можна скористатися, перепозначивши
), то нерівністю у прикладі 4.2.1 можна скористатися, перепозначивши 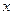 на
на 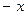 .
.
Випадок, коли всі три змінні приймають від’ємні значення зводиться до початкового доведення шляхом перепозначення 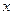 на
на 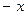 ,
, 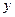 на
на 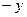 та
та 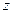 на
на 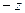 .
.
Доведення нерівності, коли одна, дві або всі три змінні приймають значення 0, очевидні.
Інше доведення даної нерівності, яке використовує ідеї координатного методу, нами було наведено у попередньому розділі (задача 3.1.2).
Задача 4.2.6. Довести нерівність
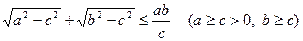 .
.
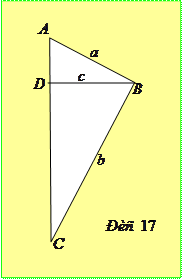 Доведення. При
Доведення. При 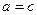 або
або 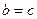 нерівність очевидна. Розглянемо випадок, коли
нерівність очевидна. Розглянемо випадок, коли 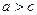 і
і 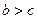 . Перепишемо нерівність у виді
. Перепишемо нерівність у виді 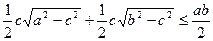 та побудуємо два прямокутні трикутники з спільним катетом
та побудуємо два прямокутні трикутники з спільним катетом 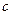 , гіпотенузи яких дорівнюють
, гіпотенузи яких дорівнюють 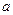 та
та 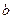 (рис. 17). Тепер ліва частина перетвореної нерівності визначатиме суму площ трикутників
(рис. 17). Тепер ліва частина перетвореної нерівності визначатиме суму площ трикутників 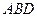 і
і 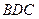 , тобто площу
, тобто площу 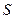 трикутника
трикутника 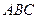 . Оскільки
. Оскільки 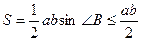 , то нерівність доведена.
, то нерівність доведена.
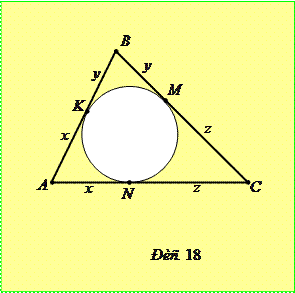
Задача 4.2.7. Довести, що 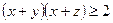 , якщо
, якщо 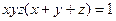 і
і 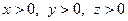 .
.
Доведення. Очевидно, що при 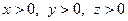 існує трикутник
існує трикутник 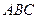 такий, що
такий, що 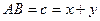 ,
, 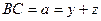 ,
, 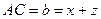 (рис. 18). Нехай точки
(рис. 18). Нехай точки 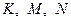 - точки дотику вписаного кола із сторонами
- точки дотику вписаного кола із сторонами 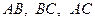 відповідно. Маємо
відповідно. Маємо 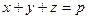 , де
, де 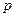 - півпериметр трикутника. Крім того,
- півпериметр трикутника. Крім того,
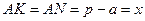 ,
, 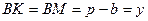 ,
, 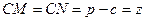 .
.
Але за умовою задачі 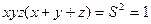 , звідки
, звідки 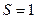 . (
. ( 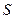 - площа трикутника
- площа трикутника 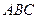 ). З іншого боку,
). З іншого боку, 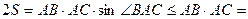
 . Тоді
. Тоді 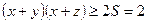 .
.
Задача 4.2.8. Довести нерівність
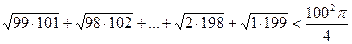 .
.
Доведення. Розглянемо четвертину круга з радіусом 100. Впишемо у нього ступінчату фігуру, яка складається з 99 прямокутників з нижньою основою, що дорівнює 1 (рис. 19). Площа першого прямокутника дорівнює
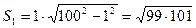 .
.
Для другого прямокутника маємо
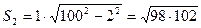 , …,
, …,
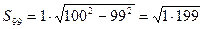 .
.
Площа ступінчатої фігури менша від площі чверті круга, тому
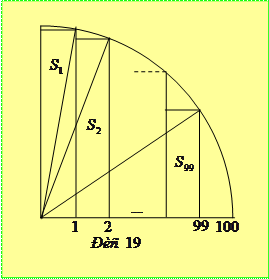
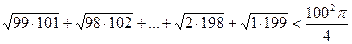 .
.
Розділ 5. Нерівності в геометрії
Геометричні фігури крім притаманних їм чисто геометричних властивостей, описуються також своїми кількісними характеристиками, зокрема довжинами відрізків, величинами кутів, площами, об’ємами, тощо. У практичній діяльності такі величини часто доводиться порівнювати, оцінювати ті межі, в яких вони змінюються (тобто аналізувати числові величини, які вони не можуть перевищувати, або не бути меншими). У результаті виникає ряд геометричних задач, пов’язаних із необхідністю оцінки геометричних величин та доведенням нерівностей, що появляються при цьому.
Окремі міркування, що стосуються певної класифікації методів доведення таких нерівностей, ми розглянемо у вигляді наступних задач.
Нерівність трикутника
Добре відомо, що для трьох довільних точок 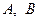 та
та 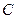 виконується нерівність
виконується нерівність 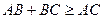 (нерівність буде строгою, якщо точка
(нерівність буде строгою, якщо точка 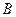 не лежать між двома іншими точками). Звідси отримуємо, що довжина ламаної не більша за відстань між її кінцями. Ці елементарні міркування часто є ключовими при доведенні нерівностей для відстаней.
не лежать між двома іншими точками). Звідси отримуємо, що довжина ламаної не більша за відстань між її кінцями. Ці елементарні міркування часто є ключовими при доведенні нерівностей для відстаней.
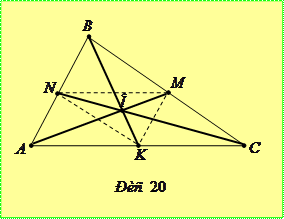 Задача 5.1.1. Довести, що довжини медіан
Задача 5.1.1. Довести, що довжини медіан 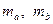 і
і 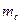 та його периметр
та його периметр 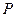 задовольняють нерівності
задовольняють нерівності
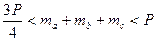 .
.
Доведення. Нехай у трикутнику 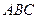
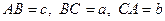 ;
; 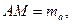
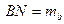 ,
, 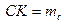 - медіани (рис. 20). Із
- медіани (рис. 20). Із 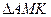 маємо
маємо
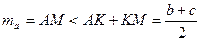 .
.
Аналогічно отримуємо нерівності 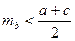 та
та 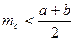 . Додаючи одержані співвідношення, отримуємо праву частину нерівності, що доводиться. Із
. Додаючи одержані співвідношення, отримуємо праву частину нерівності, що доводиться. Із  маємо
маємо
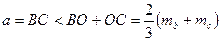 .
.
Таким же чином дістаємо нерівності 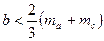 ,
, 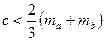 , додаючи які та попередню, отримуємо ліву частину співвідношення, що доводиться.
, додаючи які та попередню, отримуємо ліву частину співвідношення, що доводиться.
Згадуючи співвідношення, які виражають довжини медіан через сторони трикутника, зокрема 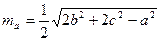 , на основі доведеного твердження можна говорити, що нами реалізовано геометричне доведення алгебраїчної нерівності
, на основі доведеного твердження можна говорити, що нами реалізовано геометричне доведення алгебраїчної нерівності
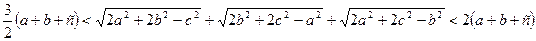 ,
,
де числа 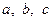 додатні і такі, що сума двох із них більша від третього.
додатні і такі, що сума двох із них більша від третього.
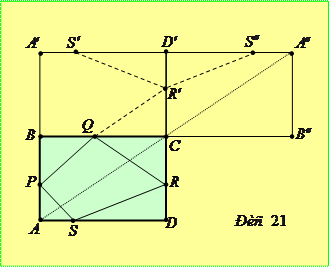
Задача 5.1.2. У прямокутнику 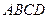 на сторонах
на сторонах 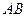 ,
, 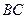 ,
, 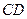 та
та 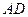 вибрано точки
вибрано точки 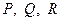 та
та 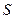 (по одній на кожній стороні). Довести, що периметр одержаного чотирикутника не менший
(по одній на кожній стороні). Довести, що периметр одержаного чотирикутника не менший 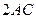 .
.
Доведення. Симетризуємо прямокутник 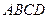 відносно сторони
відносно сторони 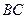 , а потім – відносно прямої
, а потім – відносно прямої 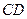 . При цьому утворяться нові прямокутники
. При цьому утворяться нові прямокутники 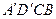 та
та 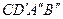 (рис. 21). Очевидно, що периметр чотирикутника
(рис. 21). Очевидно, що периметр чотирикутника 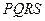 буде дорівнювати
буде дорівнювати
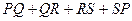 =
= 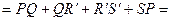
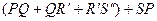
і оскільки 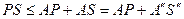 , то він не буде перевищувати довжини ламаної
, то він не буде перевищувати довжини ламаної 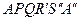 , яка в свою чергу не перевищує довжини відрізка
, яка в свою чергу не перевищує довжини відрізка 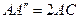 .
.
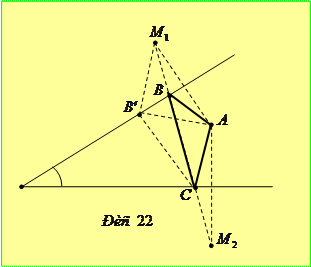
Задача 5.1.3. Дано гострий кут і точку 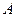 всередині нього. Знайти на сторонах кута такі точки
всередині нього. Знайти на сторонах кута такі точки 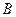 та
та 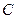 , щоб периметр трикутника
, щоб периметр трикутника 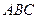 був мінімальним.
був мінімальним.
Розв’язання. Нехай задана точка 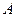 всередині кута
всередині кута 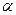 . Симетризуючи її відносно сторін кута, отримаємо точки
. Симетризуючи її відносно сторін кута, отримаємо точки 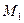 та
та 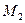 . Проведемо пряму
. Проведемо пряму 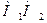 , яка перетне сторони кута у деяких точках
, яка перетне сторони кута у деяких точках 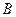 та
та 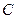 (рис. 22). Покажемо, що трикутник
(рис. 22). Покажемо, що трикутник 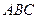 - шуканий.
- шуканий.
Насамперед, зауваживши, що симетричні відносно прямої відрізки рівні, отримуємо 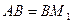 та
та 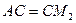 . Тому периметр
. Тому периметр
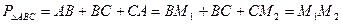 .
.
Для іншого положення точки 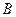 на стороні кута (наприклад, для точки
на стороні кута (наприклад, для точки 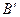 ) дістаємо
) дістаємо
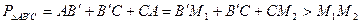 .
.
Аналогічно збільшується периметр трикутника 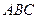 при зміні положення точки
при зміні положення точки 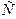 на другій стороні кута. Таким чином, точки
на другій стороні кута. Таким чином, точки 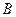 та
та 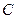 - шукані.
- шукані.
Очевидно, що якщо заданий кут гострий, то пряма 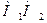 завжди перетне сторони кута, тому поставлена задача матиме єдиний розв’язок.
завжди перетне сторони кута, тому поставлена задача матиме єдиний розв’язок.
Застосування векторів
Інколи обґрунтування нерівності для відстаней зручно проводити, використовуючи вектори. При цьому може застосовуватися векторний аналог нерівності трикутника: 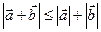 . У задачах, зв’язаних з центром ваги трикутника, використовується рівність
. У задачах, зв’язаних з центром ваги трикутника, використовується рівність 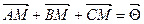 , де
, де 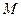 - точка перетину медіан,
- точка перетину медіан, 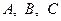 - вершини трикутника.
- вершини трикутника.
Задача 5.2.1. На площині задано два відрізки 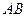 і
і 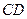 . Довести, що довжина відрізка, що сполучає їх середини, не більша за півсуму відрізків
. Довести, що довжина відрізка, що сполучає їх середини, не більша за півсуму відрізків 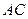 та
та 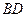 .
.
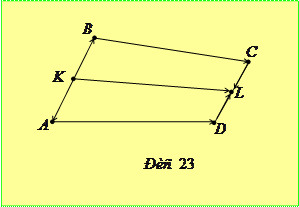 Доведення. Нехай точки
Доведення. Нехай точки 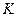 та
та 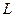 - середини відрізків
- середини відрізків 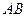 і
і 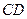 відповідно (рис. 23). Очевидно, що виконуються векторні рівності
відповідно (рис. 23). Очевидно, що виконуються векторні рівності 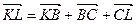 та
та 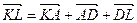 . Додаючи їх, отримуємо рівність
. Додаючи їх, отримуємо рівність 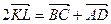 , з якої, переходячи до довжин векторів, дістаємо
, з якої, переходячи до довжин векторів, дістаємо 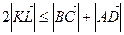 , що доводить висловлене в умові твердження. Знак рівності можливий при умові
, що доводить висловлене в умові твердження. Знак рівності можливий при умові 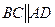 , тобто, коли заданий чотирикутник є трапецією або паралелограмом.
, тобто, коли заданий чотирикутник є трапецією або паралелограмом.
Задача 5.2.2. У чотирикутнику 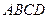 кут
кут 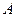 тупий,
тупий, 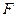 - середина сторони
- середина сторони 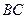 . Довести, що
. Довести, що 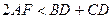 .
.
Доведення. Нехай точка 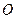 є серединою відрізка
є серединою відрізка 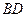 . Очевидно, що точка
. Очевидно, що точка 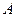 розташована всередині кола з діаметром
розташована всередині кола з діаметром 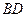 , тому
, тому 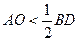 (
( 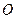 - центр кола). Оскільки
- центр кола). Оскільки 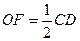 , як середня лінія трикутника
, як середня лінія трикутника 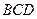 , то
, то 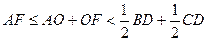 , що потрібно було довести.
, що потрібно було довести.
Задача 5.2.3. На площині задані два трикутники 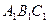 та
та 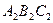 . Нехай
. Нехай 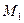 та
та 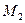 - точки перетину їхніх медіан. Довести, що
- точки перетину їхніх медіан. Довести, що 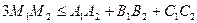 .
.
Доведення. Очевидно, що виконуються векторні рівності 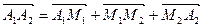 ,
,
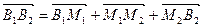 ,
,
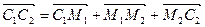 .
.
Додаючи їх, отримуємо 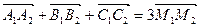 , звідки випливає нерівність, яку ми доводимо.
, звідки випливає нерівність, яку ми доводимо.
Задача 5.2.4. У піраміді 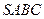 вершину
вершину 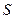 сполучили з точкою
сполучили з точкою 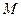 - центром ваги трикутника
- центром ваги трикутника 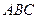 . Довести, що
. Довести, що 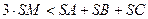 .
.
Доведення. Очевидно, що виконуються векторні рівності 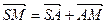 ,
, 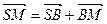 ,
, 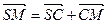 . Додаючи їх та враховуючи, що
. Додаючи їх та враховуючи, що 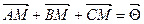 , отримуємо співвідношення
, отримуємо співвідношення 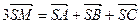 , з якого випливає задана нерівність. Знак рівності у ній неможливий, оскільки вектори
, з якого випливає задана нерівність. Знак рівності у ній неможливий, оскільки вектори 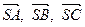 не колінеарні, тому
не колінеарні, тому 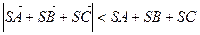 .
.
Оцінка площі
Нам відомо, що площа трикутника не перевищує половини добутку довільних двох його сторін, а площа опуклого чотирикутника - половини добутку його діагоналей. Ці факти ефективно можна використовувати при розв’язуванні окремих задач. Наведемо приклади.
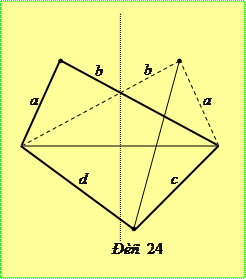 Задача 5.3.1.Нехай
Задача 5.3.1.Нехай 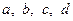 - довжини сторін опуклого чотирикутника. Довести, що його площа не перевищує
- довжини сторін опуклого чотирикутника. Довести, що його площа не перевищує 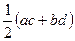 .
.
Розв’язання. Проведемо діагональ чотирикутника так, щоб по одну сторону від неї були сторони з довжинами 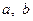 . Симетризуємо ці сторони відносно серединного перпендикуляра до проведеної діагоналі (рис. 24). Утвориться новий чотирикутник тієї ж площі, що заданий, та з довжинами послідовних сторін
. Симетризуємо ці сторони відносно серединного перпендикуляра до проведеної діагоналі (рис. 24). Утвориться новий чотирикутник тієї ж площі, що заданий, та з довжинами послідовних сторін 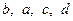 . Провівши у ньому другу діагональ, отримаємо два трикутники, площі яких не перевищують
. Провівши у ньому другу діагональ, отримаємо два трикутники, площі яких не перевищують 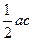 та
та 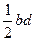 .
.
Задача 5.3.2. Периметр опуклого чотирикутника дорівнює 4. Довести, що його площа не перевищує 1.
Розв’язання. Позначимо сторони чотирикутника через 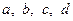 , а його площу через
, а його площу через 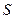 . Тоді
. Тоді 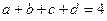 . З попередньої задачі маємо
. З попередньої задачі маємо 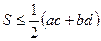 . Легко бачити, що виконується також нерівність
. Легко бачити, що виконується також нерівність 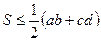 . Тоді
. Тоді
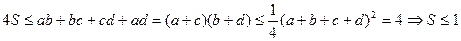 .
.
Цим самим фактично доведено, що з усіх опуклих чотирикутників із фіксованим периметром найбільшу площу має квадрат.
Задача 5.3.3. Довжини двох сторін трикутника 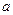 та
та 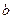 задовольняють умову
задовольняють умову 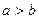 , а довжини відповідних їм висот дорівнюють
, а довжини відповідних їм висот дорівнюють 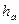 та
та 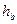 . Довести нерівність
. Довести нерівність 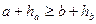 та встановити, коли досягається рівність.
та встановити, коли досягається рівність.
Доведення. Площа 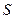 трикутника АВС дорівнює
трикутника АВС дорівнює 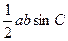 , звідки
, звідки 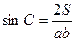 . Крім цього
. Крім цього 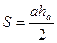 , звідки
, звідки 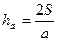 і
і 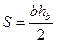 , звідки
, звідки 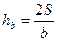 . Перетворимо нерівність, яку ми доводимо, наступним чином:
. Перетворимо нерівність, яку ми доводимо, наступним чином:
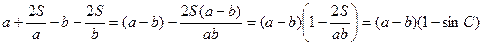 .
.
Очевидно, що, відповідно до умови задачі, одержаний вираз не може бути від’ємним. Легко бачити, що рівність досягається при 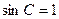 , тобто у випадку, коли трикутник прямокутний.
, тобто у випадку, коли трикутник прямокутний.
