Случайная природа действующих нагрузок

Случайная природа нагрузки обычно связана со следующими факторами.

Для технологических машин:

- рассеяние объектов производства в пределах универсальности машин и иногда вынужденное расширение регламентированного диапазона использования;

- использование машин в разных видов мелкосерийного, серийного, крупносерийного и массового производства;

- технологическое рассеяние свойств заготовок (припусков, правильности форм, твердости);

- рассеяние состояния инструмента (углов резания, затупления и др.);

- вариации технологических процессов;

- ненормальности эксплуатации. В том числе недопустимое форсирование режимов, поломка инструмента, глубокое врезание в заготовку, переохлаждение заготовки при горячей обработке.

Внутренняя динамика машин. Динамические нагрузки, возникающие:

- от работы зубчатых передач и других передач и механизмов;

- от неуравновешенности;

- от пусков;

- от остановок;

- от переключения скоростей;

перераспределения нагрузок в двух и много контактных передачах и соединениях.

Спектры нагрузок машин и отдельных деталей могут быть дискретными или непрерывными.

Дискретные спектры (смотри рисунок) представляют в координатах:

- нагрузка 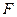– относительная продолжительность 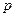ее действия (рисунок 1.22 а);

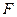- суммарная продолжительность действия нагрузки – нагрузка (рисунок 1.22 б) в порядке убывания (ранжированный спектр).

Рисунок 1.22 - Дифференциальная (а) и интегральная

(б) формы дискретного спектра нагрузок

Первая форма может рассматриваться как дифференциальная, вторая как интегральная.

Для непрерывного спектра нагрузок задают функцию плотности распределения (рисунок а) или интегральную функцию

.

Последняя физически означает долю продолжительности действия нагрузки меньше данной величины или соответствующую вероятность, что нагрузка меньше данной величины.

Практически чаще пользуются интегральными графиками непрерывных распределений (рисунок 1.23 б) в координатах ранжированного спектра, т. е. нагрузка откладывается по оси ординат, а соответственно по оси абсцисс – функция , которая означает долю продолжительности действия нагрузки больше данной величины или соответствующую вероятность.

Использование непрерывного плавного спектра в расчетах не всегда удобно, поэтому в целях упрощения функции и могут быть заменены ступенчатыми кривыми. Для этого интервал возможных нагрузок разбивают на равномерные участки . Среднее значение нагрузки 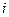-го участка обозначают через 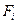. Тогда относительная продолжительность действия нагрузки 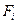равна .

Рисунок 1.23 - Дифференциальная (а) и интегральная

(б) формы непрерывного спектра нагрузок

Статистический анализ нагруженности машин различных типов показал, что при всем многообразии спектров нагрузок их можно свести к нескольким типовым. Это становится очевидным при представлении нагруженности в виде спектра относительных нагрузок, обычно выраженных в долях от максимальной нагрузки.

Функции плотности и интегральные функции спектров относительных нагрузок для типовых режимов нагружений приведены на рисунке. Для описания спектров нагрузок тяжелого (кривая 1), легкого (кривая 4) и особо легкого (кривая 5) режимов используются функции бета-распределения. Для среднего равновероятного режима (кривая 2) – функция равновероятного распределения; для среднего нормального (кривая 3) – функция нормального распределения.

Начальные моменты 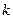-то порядка определяют по формулам:

для дискретных спектров нагрузок

,

для непрерывных спектров нагрузок

.

Начальные моменты отражают основные свойства спектра:

- начальный момент первого порядка равен среднему значению и характеризует центр группирования нагрузок спектра;

- первый и второй начальные моменты – рассеяние (дисперсию) нагрузки относительно центра группирования;

- первые три начальных момента характерезуют асимметрию распределения нагрузок.

Рисунок 1.24 - Функция плотности (а) и интегральные (б) функции спектра относительных нагрузок типовых режимов нагружения

Режимы, спектров нагрузок удобно задавать начальными моментами 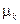. Индекс 1, 2, 3 ... в обозначении соответствует порядку начального момента.

В расчетах деталей машин на сопротивление усталости базируются на гипотезе линейного суммирования повреждений. Уточнения этой гипотезы не рассматриваются. При определении эквивалентного числа циклов перемены напряжений используют коэффициент эквивалентности циклов , равный начальному моменту 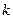- го порядка 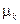, т. е. .

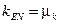При определении эквивалентной нагрузки используют коэффициент эквивалентности режима нагружений , где порядок начального момента совпадает с показателем степени 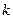, и выбирается в зависимости от показателя степени 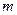кривой усталости.

Кривая усталости (кривая Велела) строится в координатах напряжение – число циклов перемен напряжений. При напряжениях, пропорциональных нагрузке, . При контактных напряжениях, пропорциональных корню квадратному из нагрузки, порядок начального момента .

Значения начальных моментов 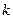-го порядка для спектров относительных нагрузок типовых режимов нагружений приведены в соответствующей литературе.

Для расчетов на прочность нагруженность может быть задана максимальной нагрузкой и соответствующим начальным моментом 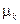спектра относительных нагрузок. Учитывая случайный характер нагрузок, обе величины должны рассматриваться в вероятностном аспекте.

Числовые значения коэффициентов вариации нагрузки должны устанавливаться применительно к отдельным отраслям машиностроения и соответствующими специалистами или организациями.

В среднем коэффициент вариации 0,1...0,15 (большие значения соответствуют машинам, рассчитанным на неопределенного потребителя).

В расчетах на сопротивление усталости коэффициент вариации нагрузки соответствует коэффициенту вариации эквивалентной нагрузки 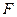, т. е. нагрузки постоянного режима нагружений эквивалентного по усталостному воздействию, рассматриваемому переменному режиму:

где – максимальная нагрузка спектра; – суммарное число циклов перемен напряжений за весь срок службы; – число циклов до перелома кривой усталости; – коэффициент эквивалентности режима нагружений; 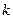– показатель степени.

Коэффициент вариации эквивалентной нагрузки 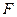, как произведение двух случайных независимых величин и , равен квадратичной сумме коэффициентов вариации максимальной нагрузки спектра и коэффициента режима :

.

Диапазон рассеяния коэффициентов эквивалентности режимов нагружения можно оценивать отношением эквивалентных нагрузок для двух смежных или ближайших несмежных типовых режимов.

Второй расчетный случай относится к универсальным машинам и к технологическим машинам, которые в связи с недостаточной нагрузкой устанавливают на заводах по выборочному размерному ряду.

Соответственно коэффициенты вариации коэффициента эквивалентности режима выбирают в пределах 0,04... 0,06 или 0,07...0,1.

Характеристику нагруженности отдельных деталей машин определяют путем пересчетов спектра нагрузок, полученного в результате измерений нагрузок на валу двигателя. Точность пересчета не всегда удовлетворительная (обычно вследствие неопределенности динамики привода), что приводит к необходимости в наиболее ответственных случаях непосредственно измерять действующие напряжения для рассчитываемой детали.

Осциллограмму с записанным изменением напряжений во времени подвергают статистической обработке с целью замены реального нагружений эквивалентным по усталостному воздействию переменным режимом с синусоидальной формой цикла напряжений.

Эквивалентную нагрузку представляют спектром относительных напряжений, т. е. расчетных напряжений 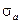, отнесенных к максимальному напряжению спектра. Способ задания относительного спектра напряжений такой же, как и для нагрузок.