Жылдамдықтарды қосу туралы теорема

Айталық, кез келген і уақыт кезеңіндегі күрделі қозғалыстағы нүкте кеңістіктін М ңүкгесінде болсын (8.1 - сурет).

Осы нүктенің абсолют жылдамдығын анықтауьш мына теорема мүмкіншілік береді.

Теорема.Күрделі қозғалыстағы нүктенің абсолют жылдамдығы оның салыстырмалы және тасымал жылдамдыктарының геометриялық косындысына тең.

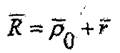Дәлелдеу.Шынында, кез келген уақыт кезеңіндегі қозғалушы нүктенің кеңістіктегі орны

(8.1)

радиус - вектормен анықталады (8.1 - суретті қара).

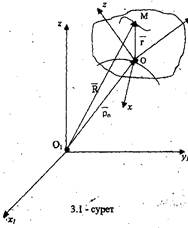8.1 - сурет

Бүл теңдіктің еркін қатты дененің козғалысындағы сөйкес теңдіктен айырлымашьшығы мүнда Ү - радиус-векторы қозғалыс кезінде бағыты мен қбса шамасын да өзгертеді.

Қозғалмайтын деп есептейтің Охуг жүйесіне қатысты М нүктесінің қозғалысы әдеттегі түрақты кеңістіктегі нүктенщ қараиайым қозғалысы болады. Демек R радиус-векторынын «қозғалмайтын» О₁ x₁ y₁ z_1, жүйесіне қатысты өзгеруі М нүктенің салыстырмаяы қозғалысын сипаттаиды, яғни нүктенің салыстырмалы жылдамдығы

, .

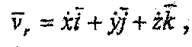(8.2)

болады. Мүнда 'і,],к - бірлік векторлар, әрине (8.2) ніамасы г радиус-векторъшың, козғалыс кезіндегі толық өзгеруі емес, ейткені rрадиус-векторы Охуz жүйесінің О нүктесін айнала қозғалуынан да өзгереді.

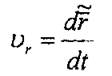Сондықтан, М нүктенің салыстырмалы қозғалысының жылдамдығы г радиус-векторының уақыт бойынша Охуг жүйесіне қатысты локалъдык немесе салыстырмалы туындысы деп аталады:

(8.3)

(8.1) векторлық теңдеудің екі жағынан да уақыт бойынша туынды алайық:

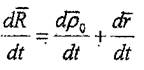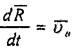(8.4)

Мұнда М нүктесінің абсолют жылдамдығы.

Бурдың формуласы бойынша

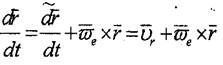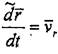(8.5)

Мұнда локальдық туынды М нүктесінің салыстырмалы жылдамдығы болып табылады.

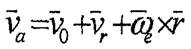Сондықтан,

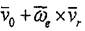(8.6)

Бірақ, нүктесінің тасымал жылдамдығы болғандықтан, соңғы теңдікті былай жаза аламыз:

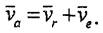. (8.7)

Сонымен теорема дәлелденді.

Абсолют жылдамдығының модулі проекциялар әдісі арқылы табылды. Ол үшін (8.4) векторлык теңдеуді қозғалмайтын О₁ x₁ y₁ z₁, санақ жүйесі өстеріне проекциялау керек:

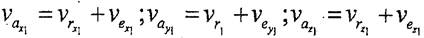(8.8)

және 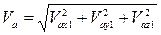(8.9)

8.1 мысал. М нүктесі үшбұрыштың АВ қабырғасы бойымен 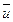жылдамдықпен қозғалады, ал үшбұрыштың өзі қозғалмайтын жазықтықпен х₁=(2+t²),м заңдылығымен қозғалады. t₁=1c мезетінде М нүктесінің абсолют жылдамдығын табу керек. u=3м/с, α=30⁰.

Шешуі. М нүктесінің қозғалмайтын жазықтыққа қатысты қозғалысын күрделі қозғалыс деп қарастырып, М нүктесінің үшбұрыштың қабырғасымен қозғалысын салыстырмалы, ал үшбұрыштың қозғалысын – тасымал қозғалыс деп таңдаймыз. Онда 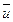- салыстырмалы жылдамдық , ал осы мезетте М нүктесімен дәлме – дәл келетін үшбұрыштың нүктесінің жылдамдығы М нүктесінің тасымал жылдамдығы болады.

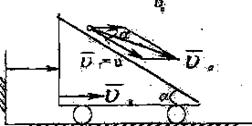8.2 - сурет

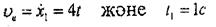Үшбүрыш ілгерілемелі қозғалыста болғандықтан, онын барлық иүктелерінің жылдамдықтары бірдей болады да, мезетінде v_e=v_g=4м/с

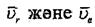, векторлары аркылы параллелограмм құрастырын, М нүктесінің абсолют жылдамдығын табамыз.

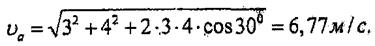3.2. Үдеулерді косу туралы теорема (Кориолис теоремасы)

Нүктенің күрделі қозгалысында үдеуін табу үшін (3.6) ернегінен уақыт бойынша толық туынды альт және Бур формуласын ескерсек, мынаны аламыз:

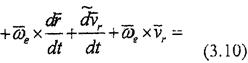
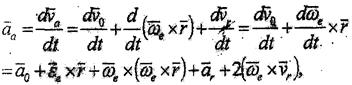
8.10

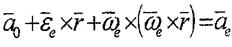Мұнда нүктенің тасымал үдеуі. Сондықтан

8.11

Немесе

8.12

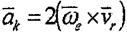мұндағы вектор - М нүктесінің салыстырмалы қозғалысы мен О,х,у^, жүйесінің О нүктесінен айнала қозғалысынан туған қосымша үдеу. Оны бұрылу үдеу немесе кориолистік үдеу депатайды.

Сонымен, курделі қозғалыстағы нуктенің удеуі оның тасымал, салыстырмалы және кориолистік удеулерінің векторлық қосындысына тең.

Бүл қорытынды удеулерді косу теоремасы немесе Кориолис теоремасы деп атайды.

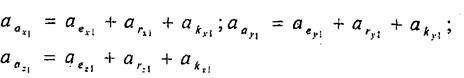Абсолют үдеудің модулі жалпы жағдайда проекциялар әдісі арықылы табылады. Ол үшін (3.12) теңдеуді қозғалмайтын өстерге проекциялау керек:

(8.14)

Онда нүктенің абсолют үдеуі

(8.15)

Кориолистік үдеудің векторы

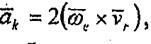(8.16)

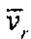
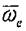
мұнда - тасымал бұрыштық жылдамдық; - салыстырмалы жылдамдык. Кориолистік үдеудің модулі мына формуламеи есептеледі:

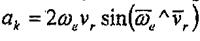
(8.17)

Кориолистік үдеудің багытың Н.Е. Жуковский ережесі арқылы анықтауға болады (3.2 - сурет):

.

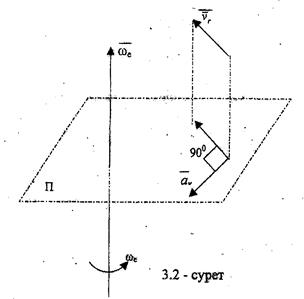8.2 – сурет

1) тасымал бұрыштық. жылдамдық векторына (немссе айналу өсіне)
перпендикуляр етіп жазықтык жүргіземіз;

2) сол жазыықтыкқа салыстырмалы жылдамдық векторының проекциясын
аламыз;

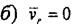
3) 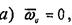салыстырмалы жылдамдық проекциясын дененің айналу бағытына
90°-қа бұрамыз.. Алынған бағыт - кориолистік үдеудің бағыты болады.

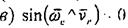Егер; яғни тасымал қозғалыс ілгерілемелі болғаны; (мысалы, салыстырмалы қозғалысының бағыты кері бағытқа ауысқан мезетте);

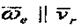
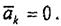, яғни , онда кориолистік үдеу .

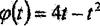8.1 мысал. Қозғалмайтын Оz өске қатысты

(өлшемдері φ-рад, t-c) заңдылығымен айналатын пластинкаға радиусы

R = 0,1м формасы жарты сақина түтікше бекітілген (8.3, а - сурет).

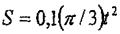
Түтікшенің ішінде (өлшемдері: S - м, t - с) заңдылығымен М нүкте қозгалады. Нүктенің мезетіндегі асболют жылдамдық пен абсолют үдеуін табу керек.

Шешуі.Қозғалмайтын Охуz координаттар жүйесінін Оz өсі пластинканын. айналу өсімен дәл келетіндей деп алайық. Қозғалушы О'ХҮZ санақ жүйесін пластинкамен байланыстырайық.

Сонымен, М нүктенің абсолют қозғалысы пластинкадағы түтікшенің ішіндегі салыстырмалы қозғалыс пен пластинканын Оz өске қатысты тасымал айналуының қосындысы болады.

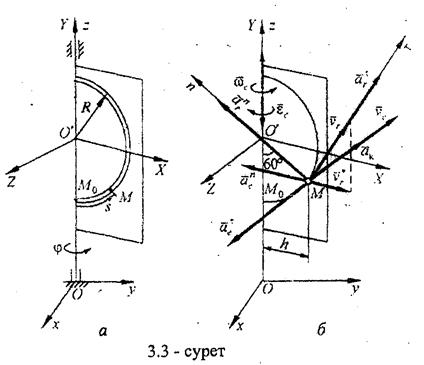8.3 - сурет

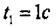Салыстырмалы қозғалыста М нүктенің траекториясы - радиусы R= 0,1м жарты шеңбер. Уақыт болғанда М нүктенің траектория бойымен орын ауыстыруы

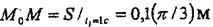болады (8.3, б - сурет). Онда

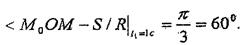Қаралып отырған уақытқа сәйкес салыстырмалы траекториядағы жанама (τ) және нормаль (n) өстерінің орнын анықтайық. Салыстырмалы жылдамдық

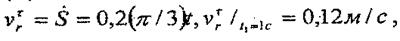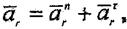салыстырмалы үдеу

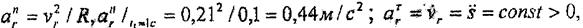мұнда

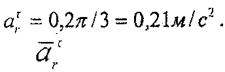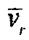және векторлар жанамамен S координаттың өсу жағына қарай
бағытталады.

Нүктенің тасымал қозғалысы - Оz өске катысты пластинкамен бірге

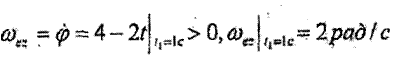
бүрыштық жылдамдықпен айналуы. Пластинканың бұрыштық үдеуі

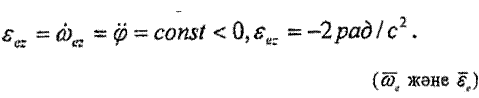
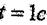Бұрыштық .жылдамдық пен бұрыштық үдеудің векторлары

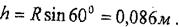8.3, б - суретте көрсетілген. мезетіндегі М нүктенің айналу өске дейін қашықтығы

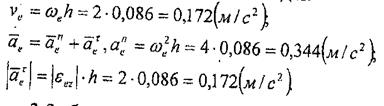. Сонымен, М нүктенің тасымал жылдамдығы мен тасымал үдеуі мына өрнектерден аныкталады:

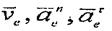векторлар 8.3, б - суретте көрсетілген.

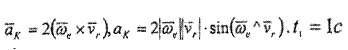Кориолистік үдеу болғанда,

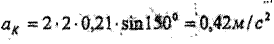
Кориолистік үдеудің бағыты Н.Е.Жуковскийдің ережесі бойынша анықталады.

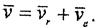Енді нүктенің абсолют жылдамдық пен абсолют үдеуін анықтайық.

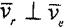Қаралып отырған жағдайда ссондықтан

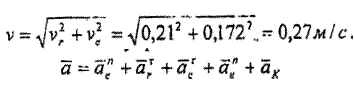
Абсолют үдеуді табу ушін

векторлық теңдестікті О¹ X,О'У,О'Z өстерге проекциялаймыз;

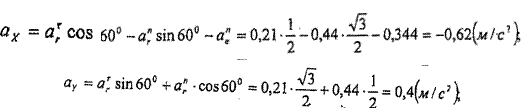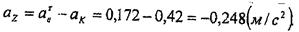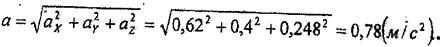Глоссарий

Нүктенің күрделі қозғалысы	Сложное движение точки	Compound motion of particle
Нүктенің абсолют қозғалысы	Абсолютное движение точки	Absolute motion of particle
Нүктенің салыстырмалы қозғалысы	Относительное движение точки	Relative motion
Нүктенің тасымал қозғалысы	Переносное движение точки	Bulk motion
Кориолистік үдеу	Ускорение Кориолиса	Coriolis acceleration
Салыстырмалы жылдамдық (үдеу)	Относительная скорость (ускорение)	Relative velocity (acceleration)
Тасымал жылдамдық (үдеу)	Переносная скорость (ускорение)	Bulk velocity (acceleration)

Такырыпқа катысты сұрақтар:

1. Қандай себептен кориолистік үдеу бар болады?

2. Қарастырылған мысалда нүктенің кориолистік үдеуі нөлге
болатын жағдайларды көрсету керек (8.3 - сурет).

3. Жер бетімен нүкте параллельмен козғалады. Кориолистік үдеу
Жердің центріне қарай бағытталған болу үшін нүкте қандай
параллельмен және қандай бағытга қозғалуға тиіс?

4. Жер бетімен нүкте меридианмен қозғалады. Қайда кориолистік үдеу
нөлге тең: полюете нсмесс экваторда ма?