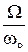Амплитудно-частотная характеристика

Рассмотрим сначала на примере испытаний нашей двухмассовой системы на вибростенде при кинематическом возбуждении 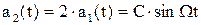(качание вокруг правой опоры) без учета сил сопротивления. Считаем, что собственные колебания уже затухли. Вынужденные колебания ищем в виде .

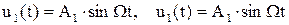После подстановки в (*), сокращения на 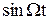и элементарных преобразований получаем

.

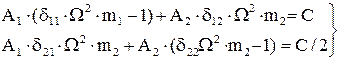Решаем полученную систему линейных алгебраических уравнений относительно А₁ и А₂. Учитываем, что коэффициенты динамичности 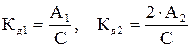, получаем

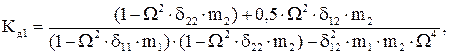
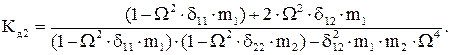
Продолжим наш пример и проанализируем результаты. Подставив в последние формулы значения податливостей и масс и, обозначив 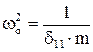(условная частота одномассовой системы, в которой вся масса сосредоточена в точке 1), получаем

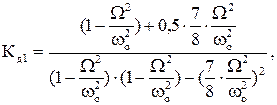
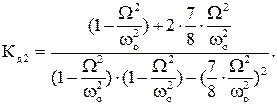
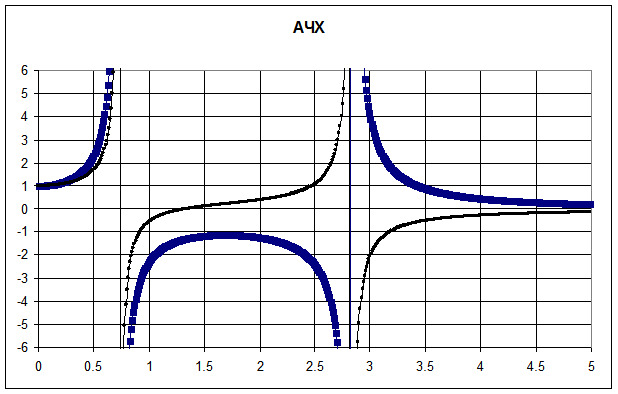
Графики АЧХ представлены на рисунке. Заметим, что существует такая частота, при которой первая масса неподвижна. Приравнивая 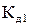к нулю, находим, что это происходит при 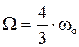. При этом вторая масса является динамическим гасителем колебаний первой массы. В общем случае величина этой массы определяется по формуле

.

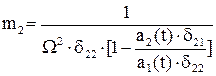Конечно, полное динамическое гашение возможно только на определенной частоте возбуждения колебаний. Однако, как видно из графика, некоторое гашение имеет место и вблизи расчетной частоты. Недостатком применения динамического гашения является увеличен6ие числа степеней свободы, т.е. число резонансных частот. В рассмотренном примере увеличение частоты возмущения может привести к резонансу, чего бы не было до установки гасителя.

В n-массовой системе построение АЧХ возможно непосредственным интегрированием системы (*) при разных частотах и видах возмущения, как с учетом, так и без учета сил сопротивления. Реализация алгоритма в конкретных случаях – также тема спецзадания во втором семестре.