Крутящий момент в сечении бруса
Кручением называют такой вид деформации бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент  (остальные факторы равны нулю).
(остальные факторы равны нулю).
Брус круглого поперечного сечения, работающий на кручение, называют валом.
Деформации кручения испытывают валы машин и механизмов при вращении, работающие пружины и т.п.
В любом поперечном сечении, перпендикулярном оси бруса, крутящий момент численно равен алгебраической суммой внешних скручивающих моментов, приложенных по одну сторону от рассматриваемого сечения. Таким образом крутящий момент  в сечении уравнивает внешние скручивающие моменты
в сечении уравнивает внешние скручивающие моменты  по одну сторону от сечения (рис. 6.1, а).
по одну сторону от сечения (рис. 6.1, а).
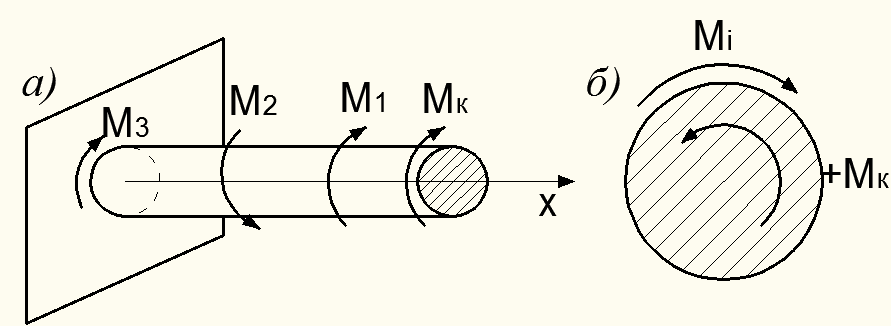
Рисунок 6.1 – Правило знаков для крутящего момента
Знак крутящего момента принципиального значения не имеет. Однако условимся в дальнейшем, что будем считать 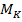 положительным, если при взгляде на торец отсеченной части бруса внешний скручивающий момент
положительным, если при взгляде на торец отсеченной части бруса внешний скручивающий момент 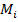 действует по часовой стрелки (рис. 6.1, б).
действует по часовой стрелки (рис. 6.1, б).
При расчете бруса на кручение в первую очередь необходимо определить все действующие на него моменты – внешние активные и реактивный при наличии защемления опорного сечения (например, 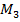 на рис. 6.1, а). Это осуществляется путем решения уравнения его равновесия
на рис. 6.1, а). Это осуществляется путем решения уравнения его равновесия
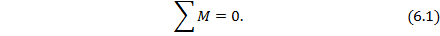
где 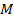 – активные и реактивные моменты, учитываемые в сечениях вала.
– активные и реактивные моменты, учитываемые в сечениях вала.
При определении крутящих моментов используется метод сечений с разбивкой бруса на участки путем проведения границ между ними. За границы принимается: концевые сечения ступеней бруса; сечения между внешними активными скручивающими моментами; сечения, где начинается или заканчивается распределенный момент.
График изменения крутящего момента по длине бруса называется эпюрой крутящих моментов. По эпюре можно определить опасное сечение, где действует наибольший по абсолютной величине крутящий момент.
Построение эпюры 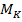 как и эпюры
как и эпюры 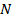 при растяжении-сжатии бруса ничем не отличаются. Положительные значения
при растяжении-сжатии бруса ничем не отличаются. Положительные значения 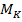 откладываются вверх от горизонтальной линии.
откладываются вверх от горизонтальной линии.
Рассмотрим принципиальную суть построения эпюры 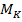 для бруса (рис. 6.2).
для бруса (рис. 6.2).
В сечении 1:
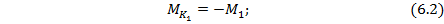
В сечении 2:
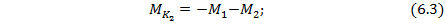
В сечении 3:
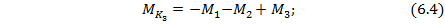
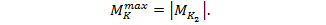
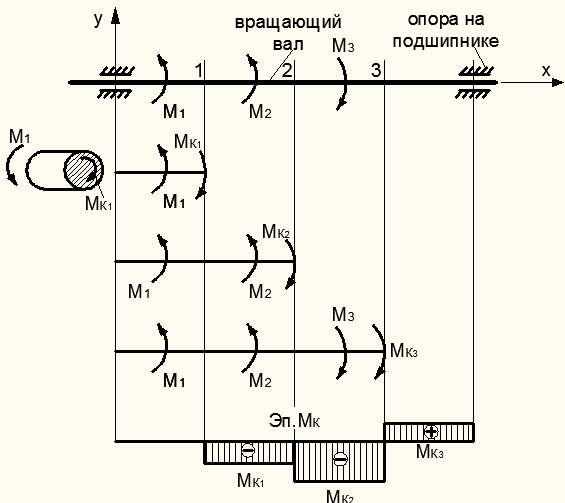
Рисунок 6.2 – Эпюра крутящих моментов для вала
Деформацию кручения испытывает равномерно вращающийся вал с насаженными на него шкивами ременной передачи.
Внешние вращающие моменты, действующие на каждый шкив, могут быть выражены через мощность 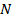 (в вт) и угловую скорость
(в вт) и угловую скорость 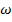 (в рад/сек) по формуле:
(в рад/сек) по формуле:
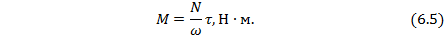
Внешний вращательный момент может быть определен и через силы натяжения ветвей ременной передачи шкивов.
Следует иметь в виду, что направление стрелок на расчетной схеме кручения бруса относятся к направлению крутящих моментов, а не к направлению вращения участков бруса.
