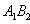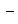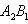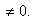Построение прямой по ее уравнению

Прямая вполне определена, если известны две принадлежащие ей точки. Для того чтобы построить прямую по ее уравнению, надо, пользуясь этим уравнением, найти координаты двух ее точек. Твердо следует помнить, что если точка принадлежит прямой, то координаты этой точки удовлетворяют уравнению прямой.

При практическом построении прямой по ее уравнению наиболее точный график получится тогда, когда координаты взятых для ее построения двух точек - целые числа.

1. Если прямая определена общим уравнением Ax + By + C = 0 и 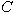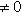, то для ее построения проще всего определить точки пересечения прямой с координатными осями.

Укажем, как определить координаты точек пересечения прямой с координатными осями. Координаты точки пересечения прямой с осью Ox находят из следующих соображений: ординаты всех точек, расположенных на оси Ox, равны нулю. В уравнении прямой полагают, что y равно нулю, и из полученного уравнения находят x. Найденное значение x и есть абсцисса точки пересечения прямой с осью Ox. Если окажется, что x = a, то координаты точки пересечения прямой с осью Ox будут (a, 0).

Чтобы определить координаты точки пересечения прямой с осью Oy, рассуждают так: абсциссы всех точек, расположенных на оси Oy, равны нулю. Взяв в уравнении прямой x равным нулю, из полученного уравнения определяют y. Найденное значение y и будет ординатой пересечения прямой с осью Oy. Если окажется, например, что y = b, то точка пересечения прямой с осью Oy имеет координаты (0, b).

Пример. Прямая 2x + y - 6 = 0 пересекает ось Ox в точке (3, 0). Действительно, взяв в этом уравнении y = 0, получим для определения x уравнение 2x - 6 = 0, откуда x = 3.

Чтобы определить точку пересечения этой прямой с осью Oy, положим в уравнении прямой x = 0. Получим уравнение y - 6 = 0, из которого следует, что y = 6. Таким образом, прямая пересекает координатные оси в точках (3, 0) и (0, 6).

Если же в общем уравнении прямой C = 0, то прямая, определяемая этим уравнением, проходит через начало координат. Таким образом, уже известна одна ее точка, и для построения прямой остается только найти еще одну ее точку. Абсциссу x этой точки задают произвольно, а ординату y находят из уравнения прямой.

Пример. Прямая 2x - 4y = 0 проходит через начало координат. Вторую точку прямой определим, взяв, например, x = 2. Тогда для определения y получаем уравнение 2*2 - 4y = 0; 4y = 4; y = 1. Итак, прямая 2x - 4y = 0 проходит через точки (0, 0) и (2, 1).

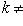
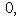
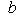
Если прямая задана уравнением y = kx + b с угловым коэффициентом, то из этого уравнения уже известна величина отрезка b, отсекаемого прямой на оси ординат, и для построения прямой остается определить координаты еще только одной точки, принадлежащей этой прямой. Если в уравнении y = kx + b 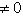, то легче всего определить координаты точки пересечения прямой с осью Ox. Выше было указано, как это сделать.

Если же в уравнении y = kx + b b = 0, то прямая проходит через начало координат, и тем самым уже известна одна принадлежащая ей точка. Чтобы найти еще одну точку, следует дать x любое значение и определить из уравнения прямой значение y, соответствующее этому значению x.

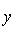
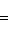
Пример. Прямая 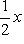проходит через начало координат и точку (2, 1), так как при x = 2 из ее уравнения .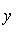

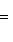
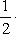
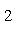
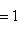Уравнение прямой, проходящей через данную точку в данном направлении. Уравнение прямой, проходящей через две данные точки. Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых. Определение точки пересечения двух прямых

1. Уравнение прямой, проходящей через данную точку A(x₁, y₁) в данном направлении, определяемом угловым коэффициентом k,

y - y₁ = k(x - x₁). (1)

Это уравнение определяет пучок прямых, проходящих через точку A(x₁, y₁), которая называется центром пучка.

2. Уравнение прямой, проходящей через две точки: A(x₁, y₁) и B(x₂, y₂), записывается так:

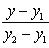
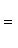
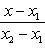
(2)

Угловой коэффициент прямой, проходящей через две данные точки, определяется по формуле

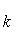
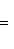
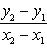
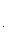(3)

3. Углом между прямыми A и B называется угол, на который надо повернуть первую прямую A вокруг точки пересечения этих прямых против движения часовой стрелки до совпадения ее со второй прямой B. Если две прямые заданы уравнениями с угловым коэффициентом

y = k₁x + B₁,

y = k₂x + B₂, (4)

то угол между ними 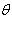определяется по формуле

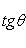
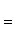
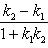
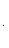(5)

Следует обратить внимание на то, что в числителе дроби из углового коэффициента второй прямой вычитается угловой коэффициент первой прямой.

Если уравнения прямой заданы в общем виде

A₁x + B₁y + C₁ = 0,

A₂x + B₂y + C₂ = 0, (6)

угол между ними определяется по формуле

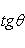
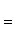
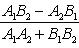
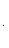(7)

4. Условия параллельности двух прямых:

а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

k₁ = k₂. (8)

б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

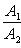
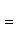
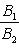
(9)

5. Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

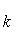
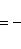
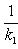
(10)

Это условие может быть записано также в виде

k₁k₂ = -1. (11)

б) Если уравнения прямых заданы в общем виде (6), то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства

A₁A₂ + B₁B₂ = 0. (12)

6. Координаты точки пересечения двух прямых находят, решая систему уравнений (6). Прямые (6) пересекаются в том и только в том случае, когда